Evaluates a sequence of Bessel functions of the first kind with real order and real positive arguments.
Required Arguments
XNU — Real
argument which is the lowest order desired. (Input)
It must be
at least zero and less than one.
X — Real argument
for which the sequence of Bessel functions is to be evaluated.
(Input)
It must be nonnegative.
N — Number of elements in the sequence. (Input)
BS — Vector of
length N
containing the values of the function through the series. (Output)
BS(I) contains the value
of the Bessel function of order XNU + I − 1 at x for
I = 1
to N.
FORTRAN 90 Interface
Generic: CALL BSJS (XNU, X, N, BS)
Specific: The specific interface names are S_BSJS and D_BSJS.
FORTRAN 77 Interface
Single: CALL BSJS (XNU, X, N, BS)
Double: The double precision name is DBSJS.
Description
The Bessel function Jv(x) is defined to be
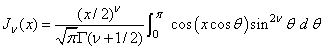
This code is based on the work of Gautschi (1964) and Skovgaard (1975). It uses backward recursion.
Comments
Workspace may be explicitly provided, if desired, by use of B2JS/DB2JS. The reference is
CALL B2JS (XNU, X, N, BS, WK)
The additional argument is
WK — work array of length 2 ∗ N.
Example
In this example, Jv(2.4048256), ν = 0, …, 10 is computed and printed.
USE BSJS_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER N
PARAMETER (N=11)
!
INTEGER K, NOUT
REAL BS(N), X, XNU
! Compute
XNU = 0.0
X = 2.4048256
CALL BSJS (XNU, X, N, BS)
! Print the results
CALL UMACH (2, NOUT)
DO 10 K=1, N
WRITE (NOUT,99999) XNU+K-1, X, BS(K)
10 CONTINUE
99999 FORMAT (' J sub ', F6.3, ' (', F6.3, ') = ', F10.3)
END
Output
J sub 0.000 ( 2.405) =
0.000
J sub 1.000 ( 2.405) = 0.519
J
sub 2.000 ( 2.405) = 0.432
J sub
3.000 ( 2.405) = 0.199
J sub 4.000 (
2.405) = 0.065
J sub 5.000 ( 2.405)
= 0.016
J sub 6.000 ( 2.405)
= 0.003
J sub 7.000 ( 2.405)
= 0.001
J sub 8.000 ( 2.405)
= 0.000
J sub 9.000 ( 2.405)
= 0.000
J sub 10.000 ( 2.405)
= 0.000
|
PHONE: 713.784.3131 FAX:713.781.9260 |