Evaluates a sequence of Bessel functions of the second kind with real nonnegative order and real positive arguments.
Required Arguments
XNU — Real
argument which is the lowest order desired. (Input)
It must be
at least zero and less than one.
X — Real positive argument for which the sequence of Bessel functions is to be evaluated. (Input)
N — Number of elements in the sequence. (Input)
BSY — Vector of
length N
containing the values of the function through the series. (Output)
BSY(I) contains the value
of the Bessel function of order I − 1 + XNU at x for
I = 1
to N.
FORTRAN 90 Interface
Generic: CALL BSYS (XNU, X, N, BSY)
Specific: The specific interface names are S_BSYS and D_BSYS.
FORTRAN 77 Interface
Single: CALL BSYS (XNU, X, N, BSY)
Double: The double precision name is DBSYS.
Description
The Bessel function Yv(x) is defined to be
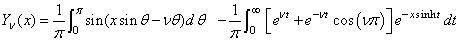
The variable ν must satisfy 0 ≤ ν < 1. If this condition
is not met, then BSY
is set to −b. In addition, x must be in 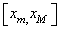 where
where 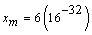 and
and 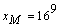 . If
. If 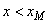 , then
−b (b = AMACH(2),
the largest representable number) is returned; and if
, then
−b (b = AMACH(2),
the largest representable number) is returned; and if 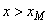 , then zero is returned.
, then zero is returned.
The algorithm is based on work of Cody and others, (see Cody et al. 1976; Cody 1969; NATS FUNPACK 1976). It uses a special series expansion for small arguments. For moderate arguments, an analytic continuation in the argument based on Taylor series with special rational minimax approximations providing starting values is employed. An asymptotic expansion is used for large arguments.
Example
In this example, Y0.015625+v−1(0.0078125), ν = 1, 2, 3 is computed and printed.
USE BSYS_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER N
PARAMETER (N=3)
!
INTEGER K, NOUT
REAL BSY(N), X, XNU
! Compute
XNU = 0.015625
X = 0.0078125
CALL BSYS (XNU, X, N, BSY)
! Print the results
CALL UMACH (2, NOUT)
DO 10 K=1, N
WRITE (NOUT,99999) XNU+K-1, X, BSY(K)
10 CONTINUE
99999 FORMAT (' Y sub ', F6.3, ' (', F6.3, ') = ', F10.3)
END
Output
Y sub 0.016 ( 0.008) = -3.189
Y sub 1.016 ( 0.008) = -88.096
Y sub 2.016 ( 0.008) = -22901.732
|
PHONE: 713.784.3131 FAX:713.781.9260 |