This function evaluates the inverse of the noncentral chi-squared cumulative function.

Function Return Value

CSNIN — Function value.   (Output)
The probability that a noncentral chi-squared random variable takes a value less than or equal to CSNIN is P.

Required Arguments

P — Probability for which the inverse of the noncentral chi-squared cumulative distribution function is to be evaluated.   (Input)
P must be in the open interval (0.0, 1.0).

DF — Number of degrees of freedom of the noncentral chi-squared distribution.   (Input)
DF must be greater than or equal to 0.5 and less than or equal to 200,000.

ALAM — The noncentrality parameter.   (Input)
ALAM must be nonnegative, and ALAM + DF must be less than or equal to 200,000.

FORTRAN 90 Interface

Generic:                              CSNIN (P, DF, ALAM)

Specific:                             The specific interface names are S_CSNIN and D_CSNIN.

FORTRAN 77 Interface

Single:                                CSNIN (P, DF, ALAM)

Double:                              The double precision name is DCSNIN.

Description

Function CSNIN evaluates the inverse distribution function of a noncentral chi-squared random variable with DF degrees of freedom and noncentrality parameter ALAM; that is, with
P = P, v = DF, and = λ = ALAM, it determines c0 (= CSNIN(P, DF, ALAM)), such that

 

 

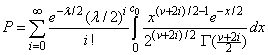
where Γ(⋅) is the gamma function. The probability that the random variable takes a value less than or equal to c0 is P .

Function CSNIN uses bisection and modified regula falsi to invert the distribution function, which is evaluated using routine CSNDF. See  CSNDF for an alternative definition of the noncentral chi-squared random variable in terms of normal random variables.

Comments

Informational error

Type Code

4         1                  Over 100 iterations have occurred without convergence. Convergence is assumed.

Example

In this example, we find the 95-th percentage point for a noncentral chi-squared random variable with 2 degrees of freedom and noncentrality parameter 1.

 

      USE CSNIN_INT

      USE UMACH_INT

      IMPLICIT   NONE

      INTEGER    NOUT

      REAL       ALAM, CHSQ, DF, P

!

      CALL UMACH (2, NOUT)

      DF   = 2.0

      ALAM = 1.0

      P    = 0.95

      CHSQ = CSNIN(P,DF,ALAM)

      WRITE (NOUT,99999) CHSQ

!

99999 FORMAT (' The 0.05 noncentral chi-squared critical value is ', &

            F6.3, '.')

!

      END

Output

 

The 0.05 noncentral chi-squared critical value is  8.642.

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260