This function evaluates the noncentral chi-squared probability density function.

Function Return Value

CSNPR — Function value, the value of the probability density function.   (Output)

Required Arguments

X — Argument for which the noncentral chi-squared probability density function is to be evaluated.   (Input)
X must be non-negative.

DF — Number of degrees of freedom of the noncentral chi-squared distribution.   (Input)
DF must be positive.

LAMBDA — Noncentrality parameter.   (Input)
LAMBDA must be non-negative.

FORTRAN 90 Interface

Generic:                              CSNPR (X, DF, LAMBDA)

Specific:                             The specific interface names are S_CSNPR and D_CSNPR.

Description

The noncentral chi-squared distribution is a generalization of the chi-squared distribution. If {Xi} are k independent, normally distributed random variables with means μi and variances σ2i, then the random variable:

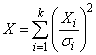
is distributed according to the noncentral chi-squared distribution. The noncentral chi-squared distribution has two parameters: k which specifies the number of degrees of freedom (i.e. the number of Xi), and λ which is related to the mean of the random variables Xi by:

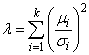
The noncentral chi-squared distribution is equivalent to a (central) chi-squared distribution with 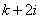 degrees of freedom, where i is the value of a Poisson distributed random variable with parameter λ ∕ 2. Thus, the probability density function is given by:

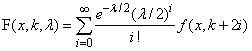
where the (central) chi-squared PDF f(x, k) is given by:

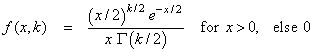
where Γ(.) is the gamma function.  The above representation of F(x, k, λ)  can be shown to be equivalent to the representation:

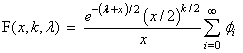
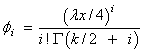
Function CSNPR (X, DF, LAMBDA) evaluates the probability density function of a noncentral chi-squared random variable with DF degrees of freedom and noncentrality parameter LAMBDA, corresponding to k = DF, λ = LAMBDA, and x = X.

Function CSNDF (X, DF, LAMBDA) evaluates the cumulative distribution function incorporating the above probability density function.

With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the central chi-squared distribution.

Example

This example calculates the noncentral chi-squared distribution for a distribution with 100 degrees of freedom and noncentrality parameter λ = 40.

 

      USE UMACH_INT

      USE CSNPR_INT

      IMPLICIT NONE

 

      INTEGER :: NOUT, I

      REAL    :: X(6)=(/ 0.0, 8.0, 40.0, 136.0, 280.0, 400.0 /)

      REAL    :: LAMBDA=40.0, DF=100.0, PDFV

 

      CALL UMACH (2, NOUT)

      WRITE (NOUT,'(//"DF: ", F4.0, "  LAMBDA: ", F4.0 //'// &

               ' "   X        PDF(X)")') DF, LAMBDA

      DO I = 1, 6

         PDFV = CSNPR(X(I), DF, LAMBDA)

         WRITE (NOUT,'(1X, F5.0, 2X, E12.5)') X(I), PDFV

      END DO

      END

Output

 

DF: 100.  LAMBDA:  40.

 

   X        PDF(X)

    0.   0.00000E+00

    8.   0.00000E+00

   40.   0.34621E-13

  136.   0.21092E-01

  280.   0.40027E-09

  400.   0.11250E-21

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260