This function evaluates the incomplete gamma function.
Function Return Value
GAMI — Function value. (Output)
Required Arguments
A — The integrand
exponent parameter. (Input)
It must be positive.
X — The upper
limit of the integral definition of GAMI.
(Input)
It must be nonnegative.
FORTRAN 90 Interface
Generic: GAMI (A, X)
Specific: The specific interface names are S_GAMI and D_GAMI.
FORTRAN 77 Interface
Single: GAMI (A, X)
Double: The double precision function name is DGAMI.
Description
The incomplete gamma function is defined to be
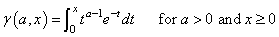
The function γ(a, x) is defined only for
a greater than zero. Although γ(a, x) is well defined for
x >-∞, this algorithm does not calculate γ(a, x) for
negative x. For large a and sufficiently large x,
γ(a, x) may overflow. γ(a, x) is bounded by
Γ(a), and users may find this bound a useful guide in determining legal
values of a.
Because logarithmic variables are used, a slight deterioration of two or three digits of accuracy will occur when GAMI is very large or very small.

Figure 4- 3 Contour Plot of γ(a, x)
Example
In this example, γ(2.5, 0.9) is computed and printed.
USE GAMI_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL A, VALUE, X
! Compute
A = 2.5
X = 0.9
VALUE = GAMI(A, X)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) A, X, VALUE
99999 FORMAT (' GAMI(', F6.3, ',', F6.3, ') = ', F6.4)
END
Output
GAMI( 2.500, 0.900) = 0.1647
|
PHONE: 713.784.3131 FAX:713.781.9260 |