Evaluates the complementary incomplete gamma function.
Function Return Value
GAMIC — Function value. (Output)
Required Arguments
A — The integrand exponent parameter as per the remarks. (Input)
X — The upper
limit of the integral definition of GAMIC.
(Input)
If A is positive, then X must be positive.
Otherwise, X
must be nonnegative.
FORTRAN 90 Interface
Generic: GAMIC (A, X)
Specific: The specific interface names are S_GAMIC and D_GAMIC.
FORTRAN 77 Interface
Single: GAMIC (A, X)
Double: The double precision function name is DGAMIC.
Description
The incomplete gamma function is defined to be
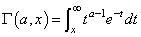
The only general restrictions on a are that it must be positive if x is zero; otherwise, it must not be too close to a negative integer such that the accuracy of the result is less than half precision. Furthermore, Γ(a, x) must not be so small that it underflows, or so large that it overflows. Although Γ(a, x) is well defined for x >-∞ and a > 0, this algorithm does not calculate Γ(a, x) for negative x.
The function GAMIC is based on a code by Gautschi (1979).
Comments
Informational error
Type Code
3 2 Result of GAMIC(A, X) is accurate to less than one-half precision because A is too near a negative integer.
Example
In this example, Γ(2.5, 0.9) is computed and printed.
USE GAMIC_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL A, VALUE, X
! Compute
A = 2.5
X = 0.9
VALUE = GAMIC(A, X)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) A, X, VALUE
99999 FORMAT (' GAMIC(', F6.3, ',', F6.3, ') = ', F6.4)
END
Output
GAMIC( 2.500, 0.900) = 1.1646
|
PHONE: 713.784.3131 FAX:713.781.9260 |