Sfun (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 5.0.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.math
Class Sfun

java.lang.Object
  com.imsl.math.Sfun

public class Sfun
extends Object
extends Object

Collection of special functions.

See Also:: Example

Field Summary
`static double`	`EPSILON_LARGE` The largest relative spacing for doubles.
`static double`	`EPSILON_SMALL` The smallest relative spacing for doubles.

Method Summary
`static double`	`beta(double a, double b)` Returns the value of the Beta function.
`static double`	`betaIncomplete(double x, double p, double q)` Returns the incomplete Beta function ratio.
`static double`	`cot(double x)` Returns the cotangent of a `double`.
`static double`	`erf(double x)` Returns the error function of a `double`.
`static double`	`erfc(double x)` Returns the complementary error function of a `double`.
`static double`	`erfcInverse(double x)` Returns the inverse of the complementary error function.
`static double`	`erfInverse(double x)` Returns the inverse of the error function.
`static double`	`fact(int n)` Returns the factorial of an integer.
`static double`	`gamma(double x)` Returns the Gamma function of a `double`.
`static double`	`log10(double x)` Returns the common (base 10) logarithm of a `double`.
`static double`	`logBeta(double a, double b)` Returns the logarithm of the Beta function.
`static double`	`logGamma(double x)` Returns the logarithm of the Gamma function of the absolute value of a `double`.
`static double`	`poch(double a, double x)` Returns a generalization of Pochhammer's symbol.
`static double`	`r9lgmc(double x)` Returns the log gamma correction term for argument values greater than or equal to 10.0.
`static double`	`sign(double x, double y)` Returns the value of x with the sign of y.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Field Detail

EPSILON_LARGE

public static final double EPSILON_LARGE

The largest relative spacing for doubles.

See Also:: Constant Field Values

EPSILON_SMALL

public static final double EPSILON_SMALL

The smallest relative spacing for doubles.

See Also:: Constant Field Values

Method Detail

beta

public static double beta(double a,
                          double b)

Returns the value of the Beta function. The beta function is defined to be

$beta (a,b) = {{Gamma (a)Gamma (b)} over {Gamma (a + b)}} = int_0^1 {t^{a - 1} } (1 - t)^{b - 1} dt$

See gamma for the definition of

The method beta requires that both arguments be positive.

Parameters:: a - a double value; b - a double value
Returns:: a double value specifying the Beta function
See Also:: Example

betaIncomplete

public static double betaIncomplete(double x,
                                    double p,
                                    double q)

Returns the incomplete Beta function ratio. The incomplete beta function is defined to be

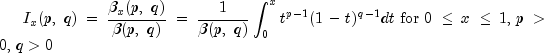
$I_x (p,,,q) = {{beta _x (p,,,q)} over {beta (p,,,q)}} = {1 over {beta (p,,,q)}}int_0^x {t^{p - 1} } (1 - t)^{q - 1} dt,,{rm{for}},,0 le x le 1,,p > 0,,q > 0$

See beta for the definition of

The parameters p and q must both be greater than zero. The argument x must lie in the range 0 to 1. The incomplete beta function can underflow for sufficiently small x and large p; however, this underflow is not reported as an error. Instead, the value zero is returned as the function value.

The method betaIncomplete is based on the work of Bosten and Battiste (1974).

Parameters:: x - a double value specifying the upper limit of integration It must be in the interval [0,1] inclusive.; p - a double value specifying the first Beta parameter. It must be positive.; q - a double value specifying the second Beta parameter. It must be positive.
Returns:: a double value specifying the incomplete Beta function ratio
See Also:: Example

cot

public static double cot(double x)

Returns the cotangent of a double.

Parameters:: x - a double value
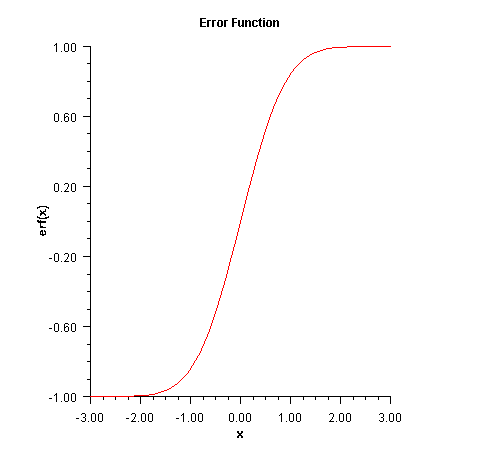
Returns:: a double value specifying the cotangent of x. If x is NaN, the result is NaN.

erf

public static double erf(double x)

Returns the error function of a double.

The error function method, erf(x), is defined to be

${rm{erf}}left( x right) = {2 over {sqrt pi }}int_0^x {e^{ - t^2 } } dt$

All values of x are legal.

Plot of erf(x)

Parameters:: x - a double value
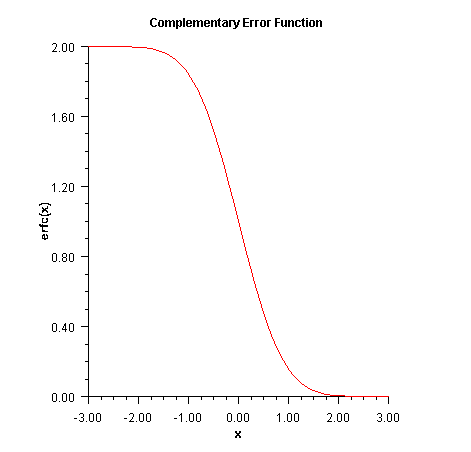
Returns:: a double value specifying the error function of x
See Also:: Example

erfc

public static double erfc(double x)

Returns the complementary error function of a double.

The complementary error function method, erfc (x), is defined to be

${rm{erfc}}left( x right) = {2 over {sqrt pi }}int_x^infty {e^{ - t^2 } } dt$

The argument x must not be so large that the result underflows. Approximately, x should be less than

${left[ -ln left( {sqrt {pi}}s right) right]}^{1/2}$

where s = Double.MIN_VALUE is the smallest representable positive floating-point number.

Plot of erfc(x)

Parameters:: x - a double value
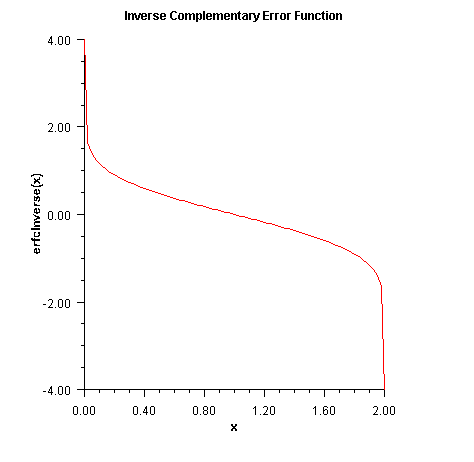
Returns:: a double value specifying the complementary error function of x
See Also:: Example

erfcInverse

public static double erfcInverse(double x)

Returns the inverse of the complementary error function.

The erfcinverse(x) method computes the inverse of the complementary error function erfc x, defined in erfc.

erfcinverse(x) is defined for . If $x_{max } lt x lt 2$ , then the answer will be less accurate than half precision. Very approximately,

$x_{it max} approx 2 - sqrt {varepsilon / (4pi)}$

where = machine precision (approximately 1.11e-16).

Plot of erfcInverse

Parameters:: x - a double value, .
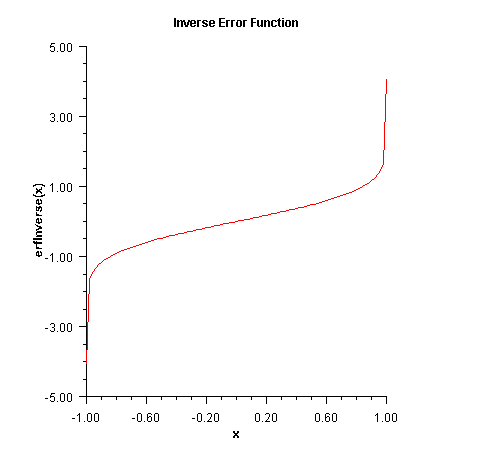
Returns:: a double value specifying the inverse of the error function of x.
See Also:: Example

erfInverse

public static double erfInverse(double x)

Returns the inverse of the error function.

erfInverse(X) method computes the inverse of the error function erf x, defined in erf.

The method erfInverse(X) is defined for $x_{it max} lt left| x right| lt 1$ , then the answer will be less accurate than half precision. Very approximately,

$x_{max } approx 1 - sqrt {varepsilon /left( {4pi } right)}$

where is the machine precision (approximately 1.11e-16).

Plot of erfinverse(x)

Parameters:: x - a double value
Returns:: a double value specifying the inverse of the error function of x
See Also:: Example

fact

public static double fact(int n)

Returns the factorial of an integer.

Parameters:: n - an int value
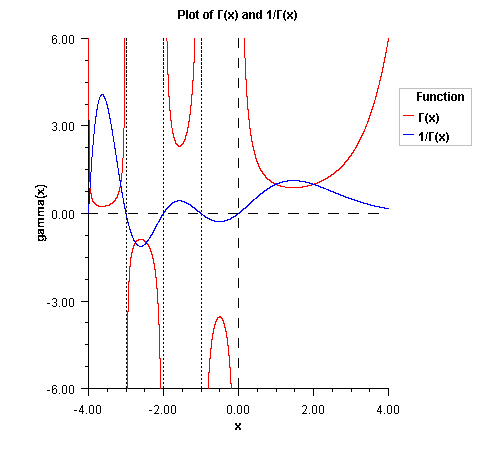
Returns:: a double value specifying the factorial of n, n!. If x is negative, the result is NaN.

gamma

public static double gamma(double x)

Returns the Gamma function of a double.

The gamma function, , is defined to be

$Gamma left( x right) = int_0^infty {t^{x - 1} } e^{ - t} dt ,,,, for , x gt 0$

For , the above definition is extended by analytic continuation.

The gamma function is not defined for integers less than or equal to zero. Also, the argument x must be greater than so that does not underflow, and x must be less than 171.64 so that does not overflow. The underflow limit occurs first for arguments that are close to large negative half integers. Even though other arguments away from these half integers may yield machine-representable values of , such arguments are considered illegal. Users who need such values should use the log gamma. Finally, the argument should not be so close to a negative integer that the result is less accurate than half precision.

Plot of gamma(x)

Parameters:: x - a double value
Returns:: a double value specifying the Gamma function of x. If x is a negative integer, the result is NaN.
See Also:: Example

log10

public static double log10(double x)

Returns the common (base 10) logarithm of a double.

Parameters:: x - a double value
Returns:: a double value specifying the common logarithm of x

logBeta

public static double logBeta(double a,
                             double b)

Returns the logarithm of the Beta function.

Method logBeta computes . See beta for the definition of .

logBeta is defined for a > 0 and b > 0. It returns accurate results even when a or b is very small. It can overflow for very large arguments; this error condition is not detected except by the computer hardware.

Parameters:: a - a double value; b - a double value
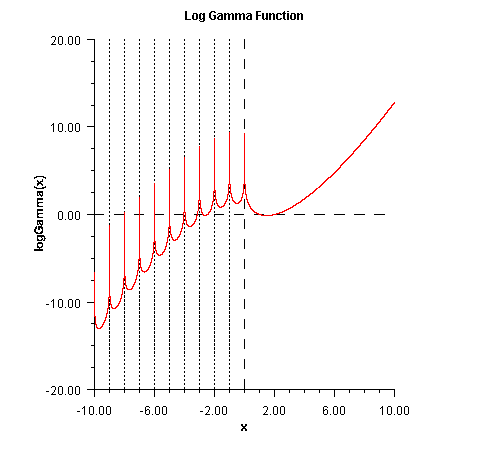
Returns:: a double value specifying the natural logarithm of the Beta function
See Also:: Example

logGamma

public static double logGamma(double x)

Returns the logarithm of the Gamma function of the absolute value of a double.

Method logGamma computes . See gamma for the definition of .

The gamma function is not defined for integers less than or equal to zero. Also, must not be so large that the result overflows. Neither should x be so close to a negative integer that the accuracy is worse than half precision.

Plot of logGamma(x)

Parameters:: x - a double value
Returns:: a double value specifying the natural logarithm of the Gamma function of . If x is a negative integer, the result is NaN.
See Also:: Example

poch

public static double poch(double a,
                          double x)

Returns a generalization of Pochhammer's symbol.

Method poch evaluates Pochhammer's symbol for n a nonnegative integer. Pochhammer's generalized symbol is defined to be

$left( a right)_x = frac{{Gamma left( {a + x} right)}}{{Gamma left( a right)}}$

See gamma for the definition of .

Note that a straightforward evaluation of Pochhammer's generalized symbol with either gamma or log gamma functions can be especially unreliable when a is large or x is small.

Substantial loss can occur if a + x or a are close to a negative integer unless is sufficiently small. To insure that the result does not overflow or underflow, one can keep the arguments a and a + x well within the range dictated by the gamma function method gamma or one can keep small whenever a is large. poch also works for a variety of arguments outside these rough limits, but any more general limits that are also useful are difficult to specify.

Parameters:: a - a double value specifying the first argument; x - a double value specifying the second, differential argument
Returns:: a double value specifying the generalized Pochhammer symbol, gamma(a+x)/gamma(a)
See Also:: Example

r9lgmc

public static double r9lgmc(double x)

Returns the log gamma correction term for argument values greater than or equal to 10.0.

Parameters:: x - a double value
Returns:: a double value specifying the log gamma correction term.

sign

public static double sign(double x,
                          double y)

Returns the value of x with the sign of y.

Parameters:: x - a double value; y - a double value
Returns:: a double value specifying the absolute value of x and the sign of y