com.imsl.stat
Class ClusterHierarchical

java.lang.Object
  com.imsl.stat.ClusterHierarchical

All Implemented Interfaces:

Serializable, Cloneable

public class ClusterHierarchical
extends Object
implements Serializable, Cloneable

Performs a hierarchical cluster analysis from a distance matrix.

Class ClusterHierarchical conducts a hierarchical cluster analysis based upon a distance matrix, or by appropriate use of the argument transform, based upon a similarity matrix. Only the upper triangular part of the dist matrix is required as input.

Hierarchical clustering in ClusterHierarchical proceeds as follows:

Initially, each data point is considered to be a cluster, numbered 1 to n = npt, where npt is the number of rows in dist.

1. If the data matrix contains similarities, they are converted to distances by the method specified by the argument transform. Set k = 1.
2. A search is made of the distance matrix to find the two closest clusters. These clusters are merged to form a new cluster, numbered n + k. The cluster numbers of the two clusters joined at this stage are saved as Right Sons and Left Sons, and the distance measure between the two clusters is stored as Cluster Level.
3. Based upon the method of clustering, updating of the distance measure in the row and column of dist corresponding to the new cluster is performed.
4. Set k = k + 1. If k is less than n, go to Step 2.

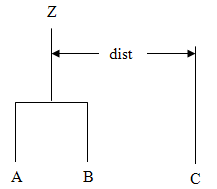
The five methods differ primarily in how the distance matrix is updated after two clusters have been joined. The argument method specifies how the distance of the cluster just merged with each of the remaining clusters will be updated. Class ClusterHierarchical allows five methods for computing the distances. To understand these measures, suppose in the following discussion that clusters A and B have just been joined to form cluster Z, and interest is in computing the distance of Z with another cluster called C.

method	Description
0	Single linkage (minimum distance). The distance from Z to C is the minimum of the distances (A to C, B to C).
1	Complete linkage (maximum distance). The distance from Z to C is the maximum of the distances (A to C, B to C).
2	Average-distance-within-clusters method. The distance from Z to C is the average distance of all objects that would be within the cluster formed by merging clusters Z and C. This average may be computed according to formulas given by Anderberg (1973, page 139).
3	Average-distance-between-clusters method. The distance from Z to C is the average distance of objects within cluster Z to objects within cluster C. This average may be computed according to methods given by Anderberg (1973, page 140).
4	Ward's method: Clusters are formed so as to minimize the increase in the within-cluster sums of squares. The distance between two clusters is the increase in these sums of squares if the two clusters were merged. A method for computing this distance from a squared Euclidean distance matrix is given by Anderberg (1973, pages 142-145).

In general, single linkage will yield long thin clusters while complete linkage will yield clusters that are more spherical. Average linkage and Ward's linkage tend to yield clusters that are similar to those obtained with complete linkage.

Function Class ClusterHierarchical produces a unique representation of the binary cluster tree via the following three conventions; the fact that the tree is unique should aid in interpreting the clusters. First, when two clusters are joined and each cluster contains two or more data points, the cluster that was initially formed with the smallest level becomes the left son. Second, when a cluster containing more than one data point is joined with a cluster containing a single data point, the cluster with the single data point becomes the right son. Finally, when two clusters containing only one object are joined, the cluster with the smallest cluster number becomes the right son.

Comments

1. The clusters corresponding to the original data points are numbered from 1 to npt, where npt is the number of rows in dist. The npt - 1 clusters formed by merging clusters are numbered npt + 1 to npt + (npt - 1 ).
2. Raw correlations, if used as similarities, should be made positive and transformed to a distance measure. One such transformation can be performed by setting argument transform, with transform = 2.
3. The user may cluster either variables or observations with ClusterHierarchical since a dissimilarity matrix, not the original data, is used. Class Dissimilarities may be used to compute the matrix dist for either the variables or observations.

See Also:

Example 1, Serialized Form

Constructor Summary

ClusterHierarchical(double[][] dist, int method, int transform)
Constructor for ClusterHierarchical.

Method Summary

int[]	getClusterLeftSons() Returns the left sons of each merged cluster.
double[]	getClusterLevel() Returns the level at which the clusters are joined.
int[]	getClusterMembership(int nClusters) Returns the cluster membership of each observation.
int[]	getClusterRightSons() Returns the right sons of each merged cluster.
int[]	getObsPerCluster(int nClusters) Returns the number of observations in each cluster.

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Detail

ClusterHierarchical

public ClusterHierarchical(double[][] dist,
                           int method,
                           int transform)

Constructor for ClusterHierarchical.

Parameters:

dist - A double symmetric matrix containing the distance (or similarity) matrix. On input, only the upper triangular part needs to be present. ClusterHierarchical saves the upper triangular part of dist in the lower triangle. On return, the upper triangular part of dist is restored, and the matrix is made symmetric.

method - An int identifying the clustering method to be used.

method	Description
0	Single linkage (minimum distance).
1	Complete linkage (maximum distance).
2	Average distance within (average distance between objects within the merged cluster).
3	Average distance between (average distance between objects in the two clusters).
4	Ward's method (minimize the within-cluster sums of squares). For Ward's method, the elements of dist are assumed to be Euclidean distances.

transform - An int identifying the type of transformation applied to the measures in dist.

transform	Description
0	No transformation is required. The elements of dist are distances.
1	Convert similarities to distances by multiplication by -1.0.
2	Convert similarities (usually correlations) to distances by taking the reciprocal of the absolute value.

Throws:

IllegalArgumentException - is thrown when the row lengths of input matrix a are not equal (i.e. the matrix edges are "jagged")

Method Detail

getClusterLeftSons

public final int[] getClusterLeftSons()

Returns the left sons of each merged cluster.

Returns:

An int array containing the left sons of each merged cluster.

getClusterLevel

public final double[] getClusterLevel()

Returns the level at which the clusters are joined.

Returns:

A double array containing the level at which the clusters are joined. Element [k-1] contains the distance (or similarity) level at which cluster npt + k was formed. If the original data in dist was transformed, the inverse transformation is applied to the returned values.

getClusterMembership

public final int[] getClusterMembership(int nClusters)

Returns the cluster membership of each observation.

Parameters:

nClusters - An int which specifies the desired number of clusters.

Returns:

An int array containing the cluster membership of each observation.

getClusterRightSons

public final int[] getClusterRightSons()

Returns the right sons of each merged cluster.

Returns:

An int array containing the right sons of each merged cluster.

getObsPerCluster

public final int[] getObsPerCluster(int nClusters)

Returns the number of observations in each cluster.

Parameters:

nClusters - An int which specifies the desired number of clusters.

Returns:

An int array containing the number of observations in each cluster.