KolmogorovOneSample (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 5.0.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class KolmogorovOneSample

java.lang.Object
  com.imsl.stat.KolmogorovOneSample

All Implemented Interfaces:: Serializable

public class KolmogorovOneSample
extends Object
implements Serializable
extends Object
implements Serializable

The class KolmogorovOneSample performs a Kolmogorov-Smirnov goodness-of-fit test in one sample.

The hypotheses tested follow:

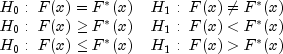
$begin{array}{ll} H_0:~ F(x) = F^{*}(x) & H_1:~F(x) ne F^{*}(x) \ H_0:~ F(x) ge F^{*}(x) & H_1:~F(x) lt F^{*}(x) \ H_0:~ F(x) le F^{*}(x) & H_1:~F(x) gt F^{*}(x) end{array}$

where

is the cumulative distribution function (CDF) of the random variable, and the theoretical cdf, $F^{*}$ , is specified via the user-supplied function cdf. Let n be the number of observations minus the number of missing observations. The test statistics for both one-sided alternatives $D_n^{+}$ and $D_n^{-}$ and the two-sided

alternative are computed as well as an asymptotic z-score and p-values associated with the one-sided and two-sided hypotheses. For

, asymptotic p-values are used (see Gibbons 1971). For

, exact one-sided p-values are computed according to a method given by Conover (1980, page 350). An approximate two-sided test p-value is obtained as twice the one-sided p-value. The approximation is very close for one-sided p-values less than 0.10 and becomes very bad as the one-sided p-values get larger.

The theoretical CDF is assumed to be continuous. If the CDF is not continuous, the statistics $D_n^{*}$ will not be computed correctly.

Estimation of parameters in the theoretical CDF from the sample data will tend to make the p-values associated with the test statistics too liberal. The empirical CDF will tend to be closer to the theoretical CDF than it should be.

No attempt is made to check that all points in the sample are in the support of the theoretical CDF. If all sample points are not in the support of the CDF, the null hypothesis must be rejected.

See Also:: Example, Serialized Form

Constructor Summary
`KolmogorovOneSample(CdfFunction cdf, double[] x)` Constructs a Kolmogorov-Smirnov goodness-of-fit test.

Method Summary
`double`	`getMaximumDifference()` Returns $D^{+}$ , the maximum difference between the theoretical and empirical CDF's.
`double`	`getMinimumDifference()` Returns $D^{-}$ , the minimum difference between the theoretical and empirical CDF's.
`int`	`getNumberMissing()` Returns the number of missing values in the data.
`int`	`getNumberOfTies()` Returns the number of ties in the data.
`double`	`getOneSidedPValue()` Probability of the statistic exceeding D under the null hypothesis of equality and against the one-sided alternative.
`double`	`getTestStatistic()` Returns $D = max(D^{+}, D^{-})$ .
`double`	`getTwoSidedPValue()` Probability of the statistic exceeding D under the null hypothesis of equality and against the two-sided alternative.
`double`	`getZ()` Returns the normalized D statistic without the continuity correction applied.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Constructor Detail

KolmogorovOneSample

public KolmogorovOneSample(CdfFunction cdf,
                           double[] x)

Constructs a Kolmogorov-Smirnov goodness-of-fit test.

Parameters:: cdf - is the cdf function, . If must be non-decreasing and its value must be in [0, 1].; x - is a double array containing the observations.

Method Detail

getMaximumDifference

public double getMaximumDifference()

Returns $D^{+}$ , the maximum difference between the theoretical and empirical CDF's.

Returns:: The value $D^{+}$ .

getMinimumDifference

public double getMinimumDifference()

Returns $D^{-}$ , the minimum difference between the theoretical and empirical CDF's.

Returns:: The value $D^{-}$ .

getNumberMissing

public int getNumberMissing()

Returns the number of missing values in the data.

Returns:: The number of missing values.

getNumberOfTies

public int getNumberOfTies()

Returns the number of ties in the data.

Returns:: the number of ties in the data

getOneSidedPValue

public double getOneSidedPValue()

Probability of the statistic exceeding D under the null hypothesis of equality and against the one-sided alternative. An exact probability is computed if the number of observation is less than or equal to 80, otherwise an approximate probability is computed.

Returns:: the one-sided probability.

getTestStatistic

public double getTestStatistic()

Returns $D = max(D^{+}, D^{-})$ .

Returns:: The value D.

getTwoSidedPValue

public double getTwoSidedPValue()

Probability of the statistic exceeding D under the null hypothesis of equality and against the two-sided alternative. This probability is twice the probability,

, reported by getOneSidedPValue, (or 1.0 if

). This approximation is nearly exact when

Returns:: the two-sided probability.

getZ

public double getZ()

Returns the normalized D statistic without the continuity correction applied.

Returns:: the value Z