MultiCrossCorrelation (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 5.0.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class MultiCrossCorrelation

java.lang.Object
  com.imsl.stat.MultiCrossCorrelation

All Implemented Interfaces:: Serializable, Cloneable

public class MultiCrossCorrelation
extends Object
implements Serializable, Cloneable
extends Object
implements Serializable, Cloneable

Computes the multichannel cross-correlation function of two mutually stationary multichannel time series.

MultiCrossCorrelation estimates the multichannel cross-correlation function of two mutually stationary multichannel time series. Define the multichannel time series X by

where

$X_j = {(X_{1j}, X_{2j}, dots, X_{nj})}^T, ;;;;; j = 1,2, dots, p$

with n = x.length and p = x[0].length. Similarly, define the multichannel time series Y by

where

$Y_j = {(Y_{1j}, Y_{2j}, dots, Y_{mj})}^T, ;;;;; j = 1,2, dots, q$

with m = y.length and q = y[0].length. The columns of X and Y correspond to individual channels of multichannel time series and may be examined from a univariate perspective. The rows of X and Y correspond to observations of p-variate and q-variate time series, respectively, and may be examined from a multivariate perspective. Note that an alternative characterization of a multivariate time series X considers the columns to be observations of the multivariate time series while the rows contain univariate time series. For example, see Priestley (1981, page 692) and Fuller (1976, page 14).

Let = xmean be the row vector containing the means of the channels of X. In particular,

$hat mu _X = (hatmu _{X_1}, hat mu _{X_2}, dots, hat mu _{X_p})$

where for j = 1, 2, ..., p

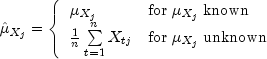
$hat mu _{X_j} = left{ begin{array}{ll} mu _{X_j} & {rm for};mu _{X_j}; {rm known} \ frac{1}{n}sumlimits_{t=1}^n {X_{tj}} & {rm for};mu _{X_j}; {rm unknown} end{array} right.$

Let

= ymean be similarly defined. The cross-covariance of lag k between channel i of X and channel j of Y is estimated by

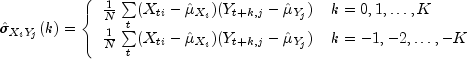
$hat sigma _{X_iY_j}(k) = left{ begin{array}{ll} frac{1}{N}sumlimits_{t}(X_{ti} - {hat mu _{X_i}})(Y_{t+k,j} - {hatmu _{Y_j}}) &{k = 0,1, dots,K} \ frac{1}{N}sumlimits_{t}(X_{ti} - {hat mu _{X_i}})(Y_{t+k,j} - {hatmu _{Y_j}}) &{k = -1,-2, dots,-K} end {array} right.$

where i = 1, ..., p, j = 1, ..., q, and K = maximum_lag. The summation on t extends over all possible cross-products with N equal to the number of cross-products in the sum.

Let = xvar, where xvar is the variance of X, be the row vector consisting of estimated variances of the channels of X. In particular,

$hat sigma _X(0) = (hat sigma _{X_1}(0), hat sigma _{X_2}(0), dots, hat sigma _{X_p}(0))$

where

$hat sigma _{X_j}(0) = frac{1}{n} sumlimits_{t = 1}^{n} {left( {X_{tj} - hat mu _{X_j}} right)}^2 {, mbox{hspace{20pt}j=0,1,dots,p}}$

Let

= yvar, where yvar is the variance of Y, be similarly defined. The cross-correlation of lag k between channel i of X and channel j of Y is estimated by

$hat rho _{X_jY_j}(k) = frac{hat sigma _{{X_j}{Y_j}(k)}}{ {[ hatsigma _{X_i}(0)hatsigma _{X_j}(0)]}^{frac{1}{2}}} ;;;;;k =0,pm1,dots, pm K$

See Also:: Example, Serialized Form

Nested Class Summary
`static class`	`MultiCrossCorrelation.NonPosVariancesException` The problem is ill-conditioned.

Constructor Summary
`MultiCrossCorrelation(double[][] x, double[][] y, int maximum_lag)` Constructor to compute the multichannel cross-correlation function of two mutually stationary multichannel time series.

Method Summary
`double[][][]`	`getCrossCorrelation()` Returns the cross-correlations between the channels of `x` and `y`.
`double[][][]`	`getCrossCovariance()` Returns the cross-covariances between the channels of `x` and `y`.
`double[]`	`getMeanX()` Returns the mean of each channel of `x`.
`double[]`	`getMeanY()` Returns the mean of each channel of `y`.
`double[]`	`getVarianceX()` Returns the variances of the channels of `x`.
`double[]`	`getVarianceY()` Returns the variances of the channels of `y`.
`void`	`setMeanX(double[] mean)` Estimate of the mean of each channel of `x`.
`void`	`setMeanY(double[] mean)` Estimate of the mean of each channel of `y`.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Constructor Detail