Bond (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 6.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.finance
Class Bond

java.lang.Object
  com.imsl.finance.Bond

public class Bond
extends Object
extends Object

Collection of bond functions.

Definitions

rate is an annualized rate of return based on the par value of the bills.

yield is an annualized rate based on the purchase price and reflects the actual yield to maturity.

coupons are interest payments on a bond.

redemption is the amount a bond pays at maturity.

frequency is the number of times a year that a bond makes interest payments.

basis is the method used to calculate dates. For example, sometimes computations are done assuming 360 days in a year.

issue is the day a bond is first sold.

settlement is the day a purchaser aquires a bond.

maturity is the day a bond's principal is repaid.

Discount Bonds

Discount bonds, also called zero-coupon bonds, do not pay interest during the life of the security, instead they sell at a discount to their value at maturity. The discount bond methods all have settlement, maturity, basis and redemption as arguments. In the following list these common arguments are omitted.

price = pricedisc(rate)
price = priceyield(yield)
price = pricemat(issue, rate, yield)
rate = disc(price)
yield = yielddisc(price)

A related method is accrintm, which returns the interest that has accumulated on the discount bond.

Treasury Bills

US Treasury bills are a special case of discount bonds. The basis is fixed for treasury bills and the redemption value is assumed to be $100. So these functions have only settlement and maturity as common arguments.

price = tbillprice(rate)
yield = tbillyield(price)
yield = tbilleq(rate)

Interest Paying Bonds

Most bonds pay interest periodically. The interest paying bond methods all have settlement, maturity, basis and frequency as arguments. Again supressing the common arguments,

price = price(rate, yield, redemption)
yield = yield(rate, price, redemption)
redemption = received(price, rate)

A related method is accrint, which returns the interest that has accumulated at settlement from the previous coupon date.

Coupon days

In this diagram, the settlement date is shown as a hollow circle and the adjacent coupon dates are shown as filled circles.

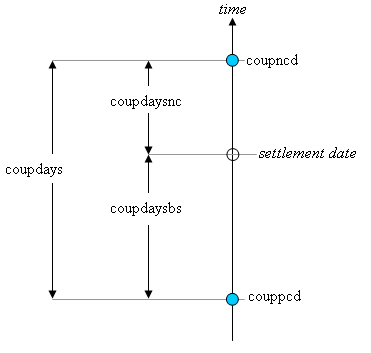
coupppcd is the coupon date immediately prior to the settlement date.
coupncd is the coupon date immediately after the settlement date.
coupdaybs is the number of days from the immediately prior coupon date to the settlement date.
coupdaysnc is the number of days from the settlement date to the next coupon date.
coupdays is the number of days between these two coupon dates.

A related method is coupnum, which returns the number of coupons payable between settlement and maturity.

Another related method is yearfrac, which returns the fraction of the year between two days.

Duration

Duration is used to measure the sensitivity of a bond to changes in interest rates. Convexity is a measure of the sensitivity of duration.

Field Summary
`static int`	`ANNUAL` Coupon payments are made annually.
`static int`	`BIMONTHLY` Coupon payments are made bimonthly (6 times per year).
`static int`	`MONTHLY` Coupon payments are made monthly.
`static int`	`QUARTERLY` Coupon payments are made quarterly.
`static int`	`SEMIANNUAL` Coupon payments are made semiannually (twice per year).

Constructor Summary
`Bond()`

Method Summary
`static double`	`accrint(GregorianCalendar issue, GregorianCalendar firstCoupon, GregorianCalendar settlement, double rate, double par, int frequency, DayCountBasis basis)` Returns the interest which has accrued on a security that pays interest periodically.
`static double`	`accrintm(GregorianCalendar issue, GregorianCalendar maturity, double rate, double par, DayCountBasis basis)` Returns the interest which has accrued on a security that pays interest at maturity.
`static double`	`amordegrc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)` Returns the depreciation for each accounting period.
`static double`	`amorlinc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)` Returns the depreciation for each accounting period.
`static double`	`convexity(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)` Returns the convexity for a security.
`static int`	`coupdaybs(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)` Returns the number of days starting with the beginning of the coupon period and ending with the settlement date.
`static double`	`coupdays(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)` Returns the number of days in the coupon period containing the settlement date.
`static int`	`coupdaysnc(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)` Returns the number of days starting with the settlement date and ending with the next coupon date.
`static GregorianCalendar`	`coupncd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)` Returns the first coupon date which follows the settlement date.
`static int`	`coupnum(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)` Returns the number of coupons payable between the settlement date and the maturity date.
`static GregorianCalendar`	`couppcd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)` Returns the coupon date which immediately precedes the settlement date.
`static double`	`disc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)` Returns the implied interest rate of a discount bond.
`static double`	`duration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)` Returns the Macauley's duration of a security where the security has periodic interest payments.
`static double`	`intrate(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double redemption, DayCountBasis basis)` Returns the interest rate of a fully invested security.
`static double`	`mduration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)` Returns the modified Macauley duration for a security with an assumed par value of $100.
`static double`	`price(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double yield, double redemption, int frequency, DayCountBasis basis)` Returns the price, per $100 face value, of a security that pays periodic interest.
`static double`	`pricedisc(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double redemption, DayCountBasis basis)` Returns the price of a discount bond given the discount rate.
`static double`	`pricemat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double yield, DayCountBasis basis)` Returns the price, per $100 face value, of a discount bond.
`static double`	`priceyield(GregorianCalendar settlement, GregorianCalendar maturity, double yield, double redemption, DayCountBasis basis)` Returns the price of a discount bond given the yield.
`static double`	`received(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double rate, DayCountBasis basis)` Returns the amount one receives when a fully invested security reaches the maturity date.
`static double`	`tbilleq(GregorianCalendar settlement, GregorianCalendar maturity, double rate)` Returns the bond-equivalent yield of a Treasury bill.
`static double`	`tbillprice(GregorianCalendar settlement, GregorianCalendar maturity, double rate)` Returns the price, per $100 face value, of a Treasury bill.
`static double`	`tbillyield(GregorianCalendar settlement, GregorianCalendar maturity, double price)` Returns the yield of a Treasury bill.
`static double`	`yearfrac(GregorianCalendar start, GregorianCalendar end, DayCountBasis basis)` Returns the fraction of a year represented by the number of whole days between two dates.
`static double`	`yield(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double price, double redemption, int frequency, DayCountBasis basis)` Returns the yield of a security that pays periodic interest.
`static double`	`yielddisc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)` Returns the annual yield of a discount bond.
`static double`	`yieldmat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double price, DayCountBasis basis)` Returns the annual yield of a security that pays interest at maturity.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Field Detail

ANNUAL

public static final int ANNUAL

Coupon payments are made annually.

See Also:: Constant Field Values

BIMONTHLY

public static final int BIMONTHLY

Coupon payments are made bimonthly (6 times per year).

See Also:: Constant Field Values

MONTHLY

public static final int MONTHLY

Coupon payments are made monthly.

See Also:: Constant Field Values

QUARTERLY

public static final int QUARTERLY

Coupon payments are made quarterly.

See Also:: Constant Field Values

SEMIANNUAL

public static final int SEMIANNUAL

Coupon payments are made semiannually (twice per year).

See Also:: Constant Field Values

Constructor Detail

Bond

public Bond()

Method Detail

accrint

public static double accrint(GregorianCalendar issue,
                             GregorianCalendar firstCoupon,
                             GregorianCalendar settlement,
                             double rate,
                             double par,
                             int frequency,
                             DayCountBasis basis)

Returns the interest which has accrued on a security that pays interest periodically. In the equation below,

represents the number of days which have accrued for the

th quasi-coupon period within the odd period. (The quasi-coupon periods are periods obtained by extending the series of equal payment periods to before or after the actual payment periods.)

represents the number of quasi-coupon periods within the odd period, rounded to the next highest integer. (The odd period is a period between payments that differs from the usual equally spaced periods at which payments are made.) ${it NL}_i$ represents the length of the normal ith quasi-coupon period within the odd period. ${it NL}_i$ is expressed in days. Function accrint can be found by solving the following:

${it par} left({{{it rate} over {it frequency}} {sumlimits_{i = 1}^{it NC} {{{{A_i } over {{it NL}_i }}}} }} right)$

Parameters:: issue - a GregorianCalendar issue date of the security; firstCoupon - a GregorianCalendar date of the security's first interest date; settlement - a GregorianCalendar settlement date of the security; rate - a double which specifies the security's annual coupon rate; par - a double which specifies the security's par value; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the accrued interest
See Also:: Example

accrintm

public static double accrintm(GregorianCalendar issue,
                              GregorianCalendar maturity,
                              double rate,
                              double par,
                              DayCountBasis basis)

Returns the interest which has accrued on a security that pays interest at maturity.

$= {it par} times {it rate} times {frac{A}{D}}$

In the above equation,

represents the number of days starting at issue date to maturity date and

represents the annual basis.

Parameters:: issue - a GregorianCalendar issue date of the security; maturity - a GregorianCalendar date of the security's maturity; rate - a double which specifies the security's annual coupon rate; par - a double which specifies the security's par value; basis - a DayCountBasis object which contains the type of day count basis to use. see DayCountBasis
Returns:: a double which specifies the accrued interest
See Also:: Example

amordegrc

public static double amordegrc(double cost,
                               GregorianCalendar issue,
                               GregorianCalendar firstPeriod,
                               double salvage,
                               int period,
                               double rate,
                               DayCountBasis basis)

Returns the depreciation for each accounting period. This method is similar to amorlinc. However, in this method a depreciation coefficient based on the asset life is applied during the evaluation of the function.

Parameters:: cost - a double which specifies the cost of the asset; issue - a GregorianCalendar issue date of the asset; firstPeriod - a GregorianCalendar date of the end of the first period; salvage - a double which specifies the asset's salvage value at the end of the life of the asset; period - an int which specifies the period; rate - a double which specifies the rate of depreciation; basis - a DayCountBasis object which contains the type of day count basis to use. see DayCountBasis.
Returns:: a double which specifies the depreciation
See Also:: Example

amorlinc

public static double amorlinc(double cost,
                              GregorianCalendar issue,
                              GregorianCalendar firstPeriod,
                              double salvage,
                              int period,
                              double rate,
                              DayCountBasis basis)

Returns the depreciation for each accounting period. This method is similar to amordegrc, except that amordegrc has a depreciation coefficient that is applied during the evaluation that is based on the asset life.

Parameters:: cost - a double which specifes the cost of the asset; issue - a GregorianCalendar issue date of the asset; firstPeriod - a GregorianCalendar date of the end of the first period; salvage - a double which specifies the asset's salvage value at the end of the life of the asset; period - an int which specifies the period; rate - a double which specifies the rate of depreciation; basis - a DayCountBasis object which contains the type of day count basis to use. see DayCountBasis.
Returns:: a double which specifies the depreciation
See Also:: Example

convexity

public static double convexity(GregorianCalendar settlement,
                               GregorianCalendar maturity,
                               double coupon,
                               double yield,
                               int frequency,
                               DayCountBasis basis)

Returns the convexity for a security. Convexity is the sensitivity of the duration of a security to changes in yield. It is computed using the following:

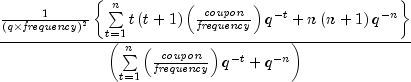
${{{1 over {left( {q times {it frequency}} right)^2 }}left{ {sumlimits_{t = 1}^n {tleft( {t + 1} right)} left( {{{it coupon} over {it frequency}}} right)q^{ - t} + nleft( {n + 1} right)q^{ - n} } right}} over {left( {sumlimits_{t = 1}^n {left( {{{it coupon} over {it frequency}}} right)q^{ - t} } + q^{ - n} } right)}}$

where n is calculated from coupnum, and

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; coupon - a double which specifies the security's annual coupon rate; yield - a double which specifires the security's annual yield; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the convexity for a security
See Also:: Example

coupdaybs

public static int coupdaybs(GregorianCalendar settlement,
                            GregorianCalendar maturity,
                            int frequency,
                            DayCountBasis basis)

Returns the number of days starting with the beginning of the coupon period and ending with the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: an int which specifies the number of days from the beginning of the coupon period to the settlement date
See Also:: Example

coupdays

public static double coupdays(GregorianCalendar settlement,
                              GregorianCalendar maturity,
                              int frequency,
                              DayCountBasis basis)

Returns the number of days in the coupon period containing the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: an int which specifies the number of days in the coupon period that contains the settlement date
See Also:: Example

coupdaysnc

public static int coupdaysnc(GregorianCalendar settlement,
                             GregorianCalendar maturity,
                             int frequency,
                             DayCountBasis basis)

Returns the number of days starting with the settlement date and ending with the next coupon date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: an int which specifies the number of days from the settlement date to the next coupon date
See Also:: Example

coupncd

public static GregorianCalendar coupncd(GregorianCalendar settlement,
                                        GregorianCalendar maturity,
                                        int frequency,
                                        DayCountBasis basis)

Returns the first coupon date which follows the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis
Returns:: an int which specifies the next coupon date after the settlement date
See Also:: Example

coupnum

public static int coupnum(GregorianCalendar settlement,
                          GregorianCalendar maturity,
                          int frequency,
                          DayCountBasis basis)

Returns the number of coupons payable between the settlement date and the maturity date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: an int which specifies the number of coupons payable between the settlement date and maturity date
See Also:: Example

couppcd

public static GregorianCalendar couppcd(GregorianCalendar settlement,
                                        GregorianCalendar maturity,
                                        int frequency,
                                        DayCountBasis basis)

Returns the coupon date which immediately precedes the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis
Returns:: an int which specifies the previous coupon date before the settlement date
See Also:: Example

disc

public static double disc(GregorianCalendar settlement,
                          GregorianCalendar maturity,
                          double price,
                          double redemption,
                          DayCountBasis basis)

Returns the implied interest rate of a discount bond. The discount rate is the interest rate implied when a security is sold for less than its value at maturity in lieu of interest payments. It is computed using the following:

In the equation above,

represents the number of days in a year based on the annual basis and

represents the number of days starting with the settlement date and ending with the maturity date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; price - a double which specifies the security's price per $100 face value; redemption - a double which specifies the security's redemption value per $100 face value; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the discount rate for a security
See Also:: Example

duration

public static double duration(GregorianCalendar settlement,
                              GregorianCalendar maturity,
                              double coupon,
                              double yield,
                              int frequency,
                              DayCountBasis basis)

Returns the Macauley's duration of a security where the security has periodic interest payments. The Macauley's duration is the weighted-average time to the payments, where the weights are the present value of the payments. It is computed using the following:

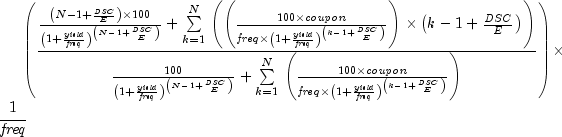
$left({{{{{left({N - 1 + {{it DSC}over E}}right)times 100}over {left({1 + {{it yield}over {it freq}}} right)^{left({N - 1 + {{it DSC}over E}}right)}}} + sumlimits_{k = 1}^N {}left({left({{{100times {it coupon}}over {{it freq}times left({1 + {{it yield}over {it freq}}}right)^{left({k - 1 + {{it DSC}over E}}right)}}}}right)timesleft({k - 1 + {{it DSC}over E}} right)}right)}over{{{100} over {left({1 + {{it yield}over {it freq}}}right)^{left(N - 1 + {{it DSC}over E}right)}}} + sum limits_{k = 1}^N {}left({{{100 times {it coupon}}over {{it freq} timesleft({1 + {{it yield}over {it freq}}}right)^{left(k - 1 + {{ it DSC}over E}right)}}}} right)}}}right)times {1over {it freq}}$

In the equation above,

represents the number of days starting with the settlement date and ending with the next coupon date.

represents the number of days within the coupon period.

represents the number of coupons payable from the settlement date to the maturity date.

represents the frequency of the coupon payments annually.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; coupon - a double which specifies the security's annual coupon rate; yield - a double which specifies the security's annual yield; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the annual duration of a security with periodic interest payments
See Also:: Example

intrate

public static double intrate(GregorianCalendar settlement,
                             GregorianCalendar maturity,
                             double investment,
                             double redemption,
                             DayCountBasis basis)

Returns the interest rate of a fully invested security. It is computed using the following:

In the equation above,

represents the number of days in a year based on the annual basis, and

represents the number of days in the period starting with the settlement date and ending with the maturity date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; investment - a double which specifies the amount invested; redemption - a double which specifies the amount to be received at maturity; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the interest rate for a fully invested security
See Also:: Example

mduration

public static double mduration(GregorianCalendar settlement,
                               GregorianCalendar maturity,
                               double coupon,
                               double yield,
                               int frequency,
                               DayCountBasis basis)

Returns the modified Macauley duration for a security with an assumed par value of $100. It is computed using the following:

where

is calculated from mduration.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; coupon - a double which specifies the security's annual coupon rate; yield - a double which specifies the security's annual yield; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the modified Macauley duration for a security with an assumed par value of $100
See Also:: Example

price

public static double price(GregorianCalendar settlement,
                           GregorianCalendar maturity,
                           double rate,
                           double yield,
                           double redemption,
                           int frequency,
                           DayCountBasis basis)

Returns the price, per $100 face value, of a security that pays periodic interest. It is computed using the following:

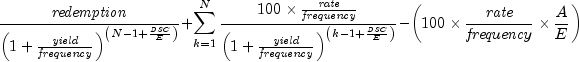
${{{it redemption} over {left( {1 + {{it yield} over {it frequency}}} right)^{left( {N - 1 + {{it DSC} over E}} right)} }}} + {sumlimits_{k = 1}^N {{{100 times {{it rate} over {it frequency}}} over {left( {1 + {{it yield} over {it frequency}}} right)^{left( {k - 1 + {{it DSC} over E}} right)} }}} } - left( {100 times {{it rate} over {it frequency}} times {A over E}} right)$

In the above equation,

represents the number of days in the period starting with the settlement date and ending with the next coupon date.

represents the number of days within the coupon period.

represents the number of coupons payable in the timeframe from the settlement date to the redemption date.

represents the number of days in the timeframe starting with the beginning of coupon period and ending with the settlement date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; rate - a double which specifies the security's annual coupon rate; yield - a double which specifies the security's annual yield; redemption - a double which specifies the security's redemption value per $100 face value; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the price per $100 face value of a security that pays periodic interest
See Also:: Example

pricedisc

public static double pricedisc(GregorianCalendar settlement,
                               GregorianCalendar maturity,
                               double rate,
                               double redemption,
                               DayCountBasis basis)

Returns the price of a discount bond given the discount rate. It is computed using the following:

In the equation above,

represents the number of days starting at the settlement date and ending with the maturity date.

represents the number of days in a year based on the annual basis.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; rate - a double which specifies the security's discount rate; redemption - a double which specifies the security's redemption value per $100 face value; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the price per $100 face value of a discounted security
See Also:: Example

pricemat

public static double pricemat(GregorianCalendar settlement,
                              GregorianCalendar maturity,
                              GregorianCalendar issue,
                              double rate,
                              double yield,
                              DayCountBasis basis)

Returns the price, per $100 face value, of a discount bond. It is computed using the following:

In the equation above,

represents the number of days in a year based on the annual basis.

represents the number of days in the period starting with the settlement date and ending with the maturity date.

represents the number of days in the period starting with the issue date and ending with the maturity date.

represents the number of days in the period starting with the issue date and ending with the settlement date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; issue - a GregorianCalendar issue date of the security; rate - a double which specifies the security's interest rate at issue date; yield - a double which specifies the security's annual yield; basis - a DayCountBasis object which contains the type of day count basis to use. see DayCountBasis
Returns:: a double which specifies the price per $100 face value of a security that pays interest at maturity
See Also:: Example

priceyield

public static double priceyield(GregorianCalendar settlement,
                                GregorianCalendar maturity,
                                double yield,
                                double redemption,
                                DayCountBasis basis)

Returns the price of a discount bond given the yield. It is computed using the following:

In the equation above,

represents the number of days starting at the settlement date and ending with the maturity date.

represents the number of days in a year based on the annual basis.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; yield - a double which specifies the security's yield; redemption - a double which specifies the security's redemption value per $100 face value; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis
Returns:: a double which specifies the price per $100 face value of a discounted security
See Also:: Example

received

public static double received(GregorianCalendar settlement,
                              GregorianCalendar maturity,
                              double investment,
                              double rate,
                              DayCountBasis basis)

Returns the amount one receives when a fully invested security reaches the maturity date. It is computed using the following:

In the equation above,

represents the number of days in a year based on the annual basis, and

represents the number of days in the period starting with the issue date and ending with the maturity date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; investment - a double which specifies the amount invested in the security; rate - a double which specifies the security's rate at issue date; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the amount received at maturity for a fully invested security
See Also:: Example

tbilleq

public static double tbilleq(GregorianCalendar settlement,
                             GregorianCalendar maturity,
                             double rate)

Returns the bond-equivalent yield of a Treasury bill. It is computed using the following:

otherwise,

${{ - {{it DSM} over {365}} + sqrt {left( {{{it DSM} over {365}}} right)^2 - left( {2 times {{it DSM} over {365}} - 1} right) times {{{it rate} times {it DSM}} over {{it rate} times {it DSM} - {360}}}} } over {{{it DSM} over {365}} - 0.5}}$

In the above equation,

represents the number of days starting at settlement date to maturity date.

Parameters:: settlement - a GregorianCalendar settlement date of the Treasury bill; maturity - a GregorianCalendar maturity date of the Treasury bill. The maturity cannot be more than a year after the settlement.; rate - a double which specifies the Treasury bill's discount rate at issue date. The discount rate is an annualized rate of return based on the par value of the bills. The discount rate is calculated on a 360-day basis (twelve 30-day months).
Returns:: a double which specifies the bond-equivalent yield for the Treasury bill. This is an annualized rate based on the purchase price of the bills and reflects the actual yield to maturity.
See Also:: Example

tbillprice

public static double tbillprice(GregorianCalendar settlement,
                                GregorianCalendar maturity,
                                double rate)

Returns the price, per $100 face value, of a Treasury bill. It is computed using the following:

In the equation above,

represents the number of days in the period starting with the settlement date and ending with the maturity date (any maturity date that is more than one calendar year after the settlement date is excluded).

Parameters:: settlement - a GregorianCalendar settlement date of the Treasury bill; maturity - a GregorianCalendar maturity date of the Treasury bill. The maturity cannot be more than a year after the settlement; rate - a double which specifies the Treasury bill's discount rate at issue date. The discount rate is an annualized rate of return based on the par value of the bills. The discount rate is calculated on a 360-day basis (twelve 30-day months).
Returns:: a double which specifies the price per $100 face value for the Treasury bill
See Also:: Example

tbillyield

public static double tbillyield(GregorianCalendar settlement,
                                GregorianCalendar maturity,
                                double price)

Returns the yield of a Treasury bill. It is computed using the following:

In the equation above,

Parameters:: settlement - a GregorianCalendar settlement date of the Treasury bill; maturity - a GregorianCalendar maturity date of the Treasury bill. The maturity cannot be more than a year after the settlement.; price - a double which specifies the Treasury bill's price per $100 face value
Returns:: a double which specifies the yield for the Treasury bill. This is an annualized rate based on the purchase price of the bills and reflects the actual yield to maturity.
See Also:: Example

yearfrac

public static double yearfrac(GregorianCalendar start,
                              GregorianCalendar end,
                              DayCountBasis basis)

Returns the fraction of a year represented by the number of whole days between two dates. It is computed using the following:

where

equals the number of days from start to end,

equals annual basis.

Parameters:: start - a GregorianCalendar start date of the security; end - a GregorianCalendar end date of the security; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the annual yield of a security that pays interest at maturity
See Also:: Example

yield

public static double yield(GregorianCalendar settlement,
                           GregorianCalendar maturity,
                           double rate,
                           double price,
                           double redemption,
                           int frequency,
                           DayCountBasis basis)

Returns the yield of a security that pays periodic interest. If there is one coupon period use the following:

{{{left( {{{it redemption} over {100}}
+ {{it rate} over {it frequency}}} right) - left[ {{{it price}
over {100}} + left( {{A over E} times {{it rate} over {it
frequency}}} right)} right]} over {{{it price} over {100}} +
left( {{A over E} times {{it rate} over {it frequency}}}
right)}}} times {{{{it frequency} times E} over {it
DSR}}}

In the equation above,

represents the number of days in the period starting with the settlement date and ending with the redemption date.

represents the number of days within the coupon period.

represents the number of days in the period starting with the beginning of coupon period and ending with the settlement date.

If there is more than one coupon period use the following:

${it price} - {{it redemption} over {left( {1 + {it yield} over {it frequency}} right)}^{N - 1 + {it DSC} over E}} - {left( {sumlimits_{k = 1}^N { {100 times {{it rate} over {it frequency}}} over {left( {1 + {it yield} over {it frequency}} right)}^{k - 1 + {it DSC} over E} }} right) } + {100 times {{it rate} over {it frequency}} times {A over E} }$

In the equation above,

represents the number of days in the period from the settlement to the next coupon date.

represents the number of days within the coupon period.

represents the number of coupons payable in the period starting with the settlement date and ending with the redemption date.

represents the number of days in the period starting with the beginning of the coupon period and ending with the settlement date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; rate - a double which specifies the security's annual coupon rate; price - a double which specifies the security's price per $100 face value; redemption - a double which specifies the security's redemption value per $100 face value; frequency - an int which specifies the number of coupon payments per year; ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the yield of a security that pays periodic interest
See Also:: Example

yielddisc

public static double yielddisc(GregorianCalendar settlement,
                               GregorianCalendar maturity,
                               double price,
                               double redemption,
                               DayCountBasis basis)

Returns the annual yield of a discount bond. It is computed using the following:

In the equation above,

represents the number of days in a year based on the annual basis, and

represents the number of days starting with the settlement date and ending with the maturity date.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; price - a double which specifies the security's price per $100 face value; redemption - a double which specifies the security's redemption value per $100 face value; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the annual yield for a discounted security
See Also:: Example

yieldmat

public static double yieldmat(GregorianCalendar settlement,
                              GregorianCalendar maturity,
                              GregorianCalendar issue,
                              double rate,
                              double price,
                              DayCountBasis basis)

Returns the annual yield of a security that pays interest at maturity. It is computed using the following:

In the equation above,

represents the number of days in the period starting with the issue date and ending with the maturity date.

represents the number of days in the period starting with the settlement date and ending with the maturity date.

represents the number of days in the period starting with the issue date and ending with the settlement date.

represents the number of days in a year based on the annual basis.

Parameters:: settlement - a GregorianCalendar settlement date of the security; maturity - a GregorianCalendar maturity date of the security; issue - a GregorianCalendar issue date of the security; rate - a double which specifies the security's interest rate at date of issue; price - a double the security's price per $100 face value; basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
Returns:: a double which specifies the annual yield of a security that pays interest at maturity
See Also:: Example

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 6.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.finance Class Bond

Definitions

Discount Bonds

Treasury Bills

Interest Paying Bonds

Coupon days

Duration

ANNUAL

BIMONTHLY

MONTHLY

QUARTERLY

SEMIANNUAL

Bond

accrint

accrintm

amordegrc

amorlinc

convexity

coupdaybs

coupdays

coupdaysnc

coupncd

coupnum

couppcd

disc

duration

intrate

mduration

price

pricedisc

pricemat

priceyield

received

tbilleq

tbillprice

tbillyield

yearfrac

yield

yielddisc

yieldmat

com.imsl.finance
Class Bond