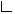 com.imsl.math.Cholesky
com.imsl.math.Cholesky
|
JMSLTM Numerical Library 6.1 | |||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | |||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | |||||||
java.lang.Objectcom.imsl.math.Cholesky
public class Cholesky
Cholesky factorization of a matrix of type double.
Class Cholesky uses the Cholesky-Banachiewicz algortithm to
factor the matrix A.
The Cholesky factorization of a matrix is ![]() ,
where R is a lower triangular matrix. Thus,
,
where R is a lower triangular matrix. Thus,
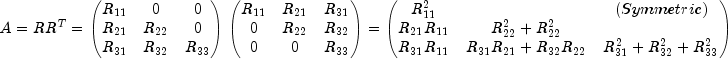
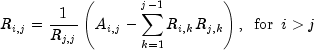
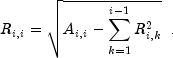
The method update is based on the LINPACK routine SCHUD;
see Dongarra et al. (1979) and updates the ![]() Cholesky factorization
of the real symmetric positive definite matrix A after a rank-one matrix is added.
Given this factorization,
Cholesky factorization
of the real symmetric positive definite matrix A after a rank-one matrix is added.
Given this factorization, update computes the factorization
![]() such that
such that
![]()
downdate, based on the LINPACK routine SCHDD;
see Dongarra et al. (1979), downdates the downdate computes the factorization ![]()
downdate determines an orthogonal matrix U as the product
![]() of Givens rotations, such that
of Givens rotations, such that
![]()
By multiplying this equation by its transpose and noting that ![]() ,
the desired result
,
the desired result
![]()
Let a be the solution of the linear system
![]() and let
and let
![]()
The Givens rotations, ![]() , are chosen such that
, are chosen such that
![]()
The ![]() , are (N + 1) by (N + 1) matrices of the form
, are (N + 1) by (N + 1) matrices of the form
![G_i =
left[ {begin{array}{*{20}c}{
I_{i - 1} } & 0 & 0 & 0 \
0 & {c_i } & 0 & { - s_i } \
0 & 0 & {I_{N - i} } & 0 \
0 & {s_i } & 0 & {c_i } \
end{array}} right]](eqn_1677.png)
The Givens rotations are then used to form
![]()
The matrix
![]()
![]()
![]()
| Nested Class Summary | |
|---|---|
static class |
Cholesky.NotSPDException
The matrix is not symmetric, positive definite. |
| Constructor Summary | |
|---|---|
Cholesky(double[][] a)
Create the Cholesky factorization of a symmetric positive definite matrix of type double. |
|
| Method Summary | |
|---|---|
void |
downdate(double[] x)
Downdates the factorization by subtracting a rank-1 matrix. |
double[][] |
getR()
Returns the R matrix that results from the Cholesky factorization. |
double[][] |
inverse()
Returns the inverse of this matrix |
double[] |
solve(double[] b)
Solve Ax = b where A is a positive definite matrix with elements of type double. |
void |
update(double[] x)
Updates the factorization by adding a rank-1 matrix. |
| Methods inherited from class java.lang.Object |
|---|
clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait |
| Constructor Detail |
|---|
public Cholesky(double[][] a)
throws SingularMatrixException,
Cholesky.NotSPDException
double.
a - a double square matrix to be factored
IllegalArgumentException - Thrown when the row lengths of matrix a are not equal
(for example, the matrix edges are "jagged".)
SingularMatrixException - Thrown when the input matrix A is singular.
Cholesky.NotSPDException - Thrown when the input matrix is not symmetric, positive definite.| Method Detail |
|---|
public void downdate(double[] x)
throws Cholesky.NotSPDException
x - A double array which specifies the rank-1 matrix.
x is not modified by this function.
Cholesky.NotSPDException - if public double[][] getR()
double matrix which contains the lower
triangular R matrix that results from the Cholesky
factorization such that public double[][] inverse()
double matrix containing the inversepublic double[] solve(double[] b)
double.
b - a double array containing the right-hand side of the linear
system
double array containing the solution to the system of
linear equationspublic void update(double[] x)
x - A double array which specifies the rank-1 matrix.
x is not modified by this function.
|
JMSLTM Numerical Library 6.1 | |||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | |||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | |||||||