com.imsl.math
Interface FeynmanKac.PdeCoefficients
- Enclosing class:
- FeynmanKac
public static interface FeynmanKac.PdeCoefficients
Public interface for user supplied PDE coefficients in the Feynman-Kac PDE.
|
Method Summary |
double |
kappa(double x,
double t)
Returns the value of the 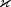 coefficient at the given point. coefficient at the given point. |
double |
mu(double x,
double t)
Returns the value of the 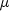 coefficient at the given point. coefficient at the given point. |
double |
sigma(double x,
double t)
Returns the value of the  coefficient at the given point. coefficient at the given point. |
double |
sigmaPrime(double x,
double t)
Returns the value of 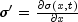 at the given point.
at the given point. |
kappa
double kappa(double x,
double t)
- Returns the value of the
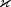 coefficient at the given point.
coefficient at the given point.
Time dependency of 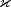 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient
algorithm because some finite element matrices do not have to be reassembled for each
t value.
- Parameters:
x - a double, the point in space at which 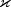 is to be evaluated.
is to be evaluated.t - a double, the time point at which 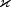 is
to be evaluated.
is
to be evaluated.
- Returns:
- a
double, the value of 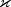 at
at (x,t).
mu
double mu(double x,
double t)
- Returns the value of the
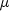 coefficient at the given point.
coefficient at the given point.
Time dependency of 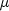 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient
algorithm because some finite element matrices do not have to be reassembled for each
t value.
- Parameters:
x - a double, the point in space at which 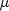 is to be evaluated.
is to be evaluated.t - a double, the time point at which 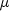 is
to be evaluated.
is
to be evaluated.
- Returns:
- a
double, the value of 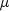 at
at (x,t).
sigma
double sigma(double x,
double t)
- Returns the value of the
 coefficient at the given point.
coefficient at the given point.
Time dependency of  can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient
algorithm because some finite element matrices do not have to be reassembled for each
t value.
- Parameters:
x - a double, the point in space at which  is to be evaluated.
is to be evaluated.t - a double, the time point at which  is
to be evaluated.
is
to be evaluated.
- Returns:
- a
double, the value of  at
at (x,t).
sigmaPrime
double sigmaPrime(double x,
double t)
- Returns the value of
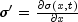 at the given point.
at the given point.
Time dependency of 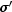 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient
algorithm because some finite element matrices do not have to be reassembled for each
t value.
- Parameters:
x - a double, the point in space at which 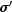 is to be evaluated.
is to be evaluated.t - a double, the time point at which 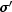 is to be evaluated.
is to be evaluated.
- Returns:
- a
double, the value of 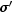 at
at
(x,t).
Copyright © 1970-2010 Visual Numerics, Inc.
Built July 30 2010.