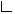ARMA (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 6.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class ARMA

java.lang.Object
  com.imsl.stat.ARMA

All Implemented Interfaces:: Serializable, Cloneable

public class ARMA
extends Object
implements Serializable, Cloneable
extends Object
implements Serializable, Cloneable

Computes least-square estimates of parameters for an ARMA model.

Class ARMA computes estimates of parameters for a nonseasonal ARMA model given a sample of observations, ${W_t}$ , for , where n = z.length.

Two methods of parameter estimation, method of moments and least squares, are provided. The user can choose a method using the setMethod method. If the user wishes to use the least-squares algorithm, the preliminary estimates are the method of moments estimates by default. Otherwise, the user can input initial estimates by using the setInitialEstimates method. The following table lists the appropriate methods for both the method of moments and least-squares algorithm:

Least Squares	Both Method of Moment and Least Squares
	`setCenter`
`setARLags`	`setMethod`
`setMALags`	`setRelativeError`
`setBackcasting`	`setMaxIterations`
`setConvergenceTolerance`	`setMean`
`setInitialEstimates`	`getMean`
`getResidual`	`getAutocovariance`
`getSSResidual`	`getVariance`
`getParamEstimatesCovariance`	`getConstant`
	`getAR`
	`getMA`

Method of Moments Estimation

Suppose the time series ${Z_t}$ is generated by an ARMA (p, q) model of the form

Let be the estimate of the mean of the time series ${Z_t}$ , where equals the following:

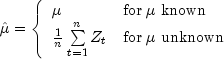
$hat mu = left{ begin{array}{ll} mu & {rm for};mu; {rm known} \ frac{1}{n}sumlimits_{t=1}^n {Z_t } & {rm for};mu; {rm unknown} end{array} right.$

The autocovariance function is estimated by

$hat sigma left( k right) = frac{1}{n} sumlimits_{t = 1}^{n - k} {left( {Z_t - hat mu } right)} left( {Z_{t + k} - hat mu } right)$

for , where K = p + q. Note that is an estimate of the sample variance.

Given the sample autocovariances, the function computes the method of moments estimates of the autoregressive parameters using the extended Yule-Walker equations as follows:

where

$hat phi = left( {hat phi _1 ,; ldots ,;hat phi _p } right)^T$

$hat Sigma _{ij} = hat sigma left( {|q + i - j|} right), ,,, i,j = 1, , ldots , , p$

$hat sigma _i = hat sigma left( {q + i} right), ,,, i = 1,; ldots ,;p$

The overall constant is estimated by the following:

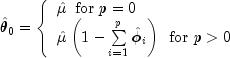
$hat theta _0 = left{ begin{array}{l} hat mu ,,, {rm{for}} ,, p = 0 \ hat mu left( {1 - sumlimits_{i = 1}^p {hat phi _i } } right) ,,, {rm{for}} ,, p > 0 \ end{array} right.$

The moving average parameters are estimated based on a system of nonlinear equations given K = p + q + 1 autocovariances, , and p autoregressive parameters for .

Let . The autocovariances of the derived moving average process are estimated by the following relation:

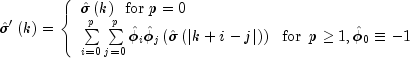
$hat sigma 'left( k right) = left{ begin{array}{l} hat sigma left( k right) ,,, {rm{for}} ,, p = 0 \ sumlimits_{i = 0}^p {sumlimits_{j = 0}^p {hat phi _i hat phi _j } left( {hat sigma left( {left| {k + i - j} right|} right)} right) ,,,, {rm{for}} ,,, p ge 1,hat phi _0 equiv - 1} \ end{array} right.$

The iterative procedure for determining the moving average parameters is based on the relation

$sigma left( k right) = left{ begin{array}{l} left( {1 + theta _1^2 + ; ldots ; + theta _q^2 } right)sigma _A^2 ,,,, {rm{for}} ,,, k = 0 \ left( { - theta _k + theta _1 theta _{k + 1} + ; ldots ; + theta _{q - k} theta _q } right)sigma _A^2 ,,,, {rm{for}} ,,, k ge 1 \ end{array} right.$

where denotes the autocovariance function of the original process.

Let and , where

$tau _j = left{ begin{array}{l} sigma _A ,,,, {rm{for}} ,,, j = 0 \ - theta _j /tau _0 ,,,, {rm{for}} ,,, j = 1,; ldots ,;q \ end{array} right.$

and

$f_j = sumlimits_{i = 0}^{q - j} {tau _i } tau _{i + j} - hat sigma 'left( j right) ,,,, {rm{for}} ,,, j = 0,;1,; ldots ,;q$

Then, the value of at the (i + 1)-th iteration is determined by the following:

$tau ^{i + 1} = tau ^i - left( {T^i } right)^{ - 1} f^i$

The estimation procedure begins with the initial value

$tau ^0 = (sqrt {hat sigma 'left( 0 right),} quad 0,; ldots ,;0)^T$

and terminates at iteration i when either $left| {f^i } right|$ is less than relativeError or i equals iterations. The moving average parameter estimates are obtained from the final estimate of by setting

$hat theta _j = - tau _j /tau _0 ,,,, {rm{for}} ,,, j = 1,; ldots ,;q$

The random shock variance is estimated by the following:

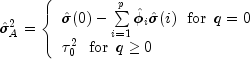
$hat sigma _A^2 = left{ begin{array}{l} hat sigma (0) - sumlimits_{i = 1}^p {hat phi _i hat sigma (i) ,,,, {rm{for}} ,,, q = 0} \ tau _0^2 ,,,, {rm{for}} ,,, q ge 0 \ end{array} right.$

See Box and Jenkins (1976, pp. 498-500) for a description of a function that performs similar computations.

Least-squares Estimation

Suppose the time series ${Z_t}$ is generated by a nonseasonal ARMA model of the form,

$phi (B) (Z_t - mu) = theta(B)A_t ,,,, {rm{for}} ,,t in {0, pm 1, pm 2, ldots}$

where B is the backward shift operator, is the mean of , and

$phi left( B right) = 1 - phi _1 B^{l_phi left( 1 right)} - phi _2 B^{l_phi left( 2 right)} - ;...; - phi _p B^{l_phi left( p right)} quad ,,,, {rm{for}} ,,, p ge 0$

${rm{theta }}left( B right) = 1 - {rm{theta }}_1 B^{l_theta left( 1 right)} - {rm{theta }}_2 B^{l_theta left( 2 right)} - ;...; - {rm{theta }}_q B^{l_theta left( q right)} quad ,,,, {rm{for}} ,,, q ge 0$

with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:

so that the nonseasonal ARMA model is of order , where and . Note that the usual hierarchical model assumes the following:

Consider the sum-of-squares function

$S_T left( {mu ,phi ,theta } right) = sumlimits_{ - T + 1}^n {left[ {A_t } right]^2 }$

where

$left[ {A_t } right] = Eleft[ {A_t left| {left( {mu ,phi ,theta ,Z} right)} right.} right]$

and T is the backward origin. The random shocks ${A_t}$ are assumed to be independent and identically distributed

$N left( {0,sigma _A^2 } right)$

random variables. Hence, the log-likelihood function is given by

$lleft( {mu ,phi ,theta ,sigma _A } right) = fleft( {mu ,phi ,theta } right) - nln left( {sigma _A } right) - frac{{S_T left( {mu ,phi ,theta } right)}} {{2sigma _A^2 }}$

where is a function of .

For T = 0, the log-likelihood function is conditional on the past values of both and required to initialize the model. The method of selecting these initial values usually introduces transient bias into the model (Box and Jenkins 1976, pp. 210-211). For , this dependency vanishes, and estimation problem concerns maximization of the unconditional log-likelihood function. Box and Jenkins (1976, p. 213) argue that

$S_infty left( {mu ,phi ,theta } right)/left( {2sigma _A^2 } right)$

dominates

$lleft( {mu ,phi ,theta ,sigma _A^2 } right)$

The parameter estimates that minimize the sum-of-squares function are called least-squares estimates. For large n, the unconditional least-squares estimates are approximately equal to the maximum likelihood-estimates.

In practice, a finite value of T will enable sufficient approximation of the unconditional sum-of-squares function. The values of needed to compute the unconditional sum of squares are computed iteratively with initial values of obtained by back forecasting. The residuals (including backcasts), estimate of random shock variance, and covariance matrix of the final parameter estimates also are computed. ARIMA parameters can be computed by using Difference with ARMA.

Forecasting

The Box-Jenkins forecasts and their associated probability limits for a nonseasonal ARMA model are computed given a sample of n = z.length, ${Z_t}$ for .

Suppose the time series is generated by a nonseasonal ARMA model of the form

for , where B is the backward shift operator, is the constant, and

$phi left( B right) = 1 - phi _1 B^{l_phi left( 1 right)} - phi _2 B^{l_phi left( 2 right)} - ; ldots ; - phi _p B^{l_phi left( p right)}$

$theta left( B right) = 1 - theta _1 B^{l_theta left( 1 right)} - theta _2 B^{l_theta left( 2 right)} - ; ldots ; - theta _q B^{l_theta left( q right)}$

with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:

so that the nonseasonal ARMA model is of order , where ${p'}= l_theta(p)$ and ${q'}= l_theta(q)$ . Note that the usual hierarchical model assumes the following:

The Box-Jenkins forecast at origin t for lead time l of $Z_{t+1}$ is defined in terms of the difference equation

$hat Z_t left( l right) = theta _0 + phi _1 left[ {Z_{t + l - l_phi left( 1 right)} } right] + ; ldots ; + phi _p left[ {Z_{t + l - l_phi left( p right)} } right]$

$+ left[ {A_{t + l} } right] - theta _1 left[ {A_{t + l - l_theta left( 1 right)} } right]; - ; ldots ; - theta _q left[ {A_{t + l - l_theta left( q right)} } right]$

where the following is true:

$left[ {Z_{t + k} } right] = left{ begin{array}{l}Z_{t + k} ,,,, {rm{for}} ,,, k = 0,; - 1,; - 2,; ldots \ hat Z_t left( k right) ,,,, {rm{for}} ,,, k = 1,;2,; ldots \ end{array} right.$

$left[ {A_{t + k} } right] = left{ begin{array}{l} Z_{t + k} - hat Z_{t + k - 1} left( 1 right) ,,,, {rm{for}} ,,, k = 0,; - 1,; - 2,;... \ 0 ,,,, {rm{for}} ,,, k = 1,;2,;... \ end{array} right.$

The percent probability limits for $Z_{t+l}$ are given by

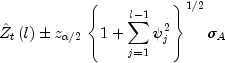
$hat Z_t left( l right) pm z_{alpha/2} left{ {1 + sumlimits_{j = 1}^{l - 1} {psi _j^2 } } right}^{1/2} sigma _A$

where $z_{alpha/2}$ is the percentile of the standard normal distribution

and

$left{ {psi _j^2 } right}$

are the parameters of the random shock form of the difference equation. Note that the forecasts are computed for lead times at origins , where and .

The Box-Jenkins forecasts minimize the mean-square error

$Eleft[ {Z_{t + l} - hat Z_t left( l right)} right]^2$

Also, the forecasts can be easily updated according to the following equation:

$hat Z_{t + 1} left( l right) = hat Z_t left( {l + 1} right) + psi _l A_{t + 1}$

This approach and others are discussed in Chapter 5 of Box and Jenkins (1976).

See Also:: Example 1, Example 2, Example 3, Serialized Form

Nested Class Summary
`static class`	`ARMA.IllConditionedException` The problem is ill-conditioned.
`static class`	`ARMA.IncreaseErrRelException` The bound for the relative error is too small.
`static class`	`ARMA.MatrixSingularException` The input matrix is singular.
`static class`	`ARMA.NewInitialGuessException` The iteration has not made good progress.
`static class`	`ARMA.NoProgressException` The algorithm is not making any progress, try new initial guess.
`static class`	`ARMA.TooManyCallsException` The number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.
`static class`	`ARMA.TooManyFcnEvalException` Maximum number of function evaluations exceeded.
`static class`	`ARMA.TooManyITNException` Maximum number of iterations exceeded.
`static class`	`ARMA.TooManyJacobianEvalException` Maximum number of Jacobian evaluations exceeded.

Field Summary
`static int`	`LEAST_SQUARES` Indicates autoregressive and moving average parameters are estimated by a least-squares procedure.
`static int`	`METHOD_OF_MOMENTS` Indicates autoregressive and moving average parameters are estimated by a method of moments procedure.

Constructor Summary
`ARMA(int p, int q, double[] z)` Constructor for `ARMA`.

Method Summary
`void`	`compute()` Computes least-square estimates of parameters for an ARMA model.
`double[][]`	`forecast(int nForecast)` Computes forecasts and their associated probability limits for an ARMA model.
`double[]`	`getAR()` Returns the final autoregressive parameter estimates.
`double[]`	`getAutoCovariance()` Returns the autocovariances of the time series `z`.
`int`	`getBackwardOrigin()` Returns the user-specified backward origin
`double`	`getConstant()` Returns the constant parameter estimate.
`double[]`	`getDeviations()` Returns the deviations used for calculating the forecast confidence limits.
`double[]`	`getForecast(int nForecast)` Returns forecasts
`double`	`getInnovationVariance()` Returns the variance of the random shock.
`double[]`	`getMA()` Returns the final moving average parameter estimates.
`double`	`getMean()` Returns an update of the mean of the time series `z`.
`int`	`getNumberOfBackcasts()` Returns the number of backcasts used to calculate the AR coefficients for the time series `z`.
`double[][]`	`getParamEstimatesCovariance()` Returns the covariances of parameter estimates.
`double[]`	`getPsiWeights()` Returns the psi weights of the infinite order moving average form of the model.
`double[]`	`getResidual()` Returns the residuals.
`double`	`getSSResidual()` Returns the sum of squares of the random shock.
`double`	`getVariance()` Returns the variance of the time series `z`.
`void`	`setARLags(int[] arLags)` Sets the order of the autoregressive parameters.
`void`	`setArmaInfo(double constant, double[] ar, double[] ma, double var)` Sets the ARMA_Info Object to previously determined values
`void`	`setBackcasting(int maxBackcast, double tolerance)` Sets backcasting option.
`void`	`setBackwardOrigin(int backwardOrigin)` Sets the maximum backward origin.
`void`	`setCenter(boolean center)` Sets center option.
`void`	`setConfidence(double confidence)` Sets the confidence level for calculating confidence limit deviations returned from `getDeviations`.
`void`	`setConvergenceTolerance(double convergenceTolerance)` Sets the tolerance level used to determine convergence of the nonlinear least-squares algorithm.
`void`	`setInitialEstimates(double[] ar, double[] ma)` Sets preliminary estimates for the `LEAST_SQUARES` estimation method.
`void`	`setMALags(int[] maLags)` Sets the order of the moving average parameters.
`void`	`setMaxIterations(int iterations)` Sets the maximum number of iterations.
`void`	`setMean(double zMean)` Sets an initial estimate of the mean of the time series `z`.
`void`	`setMethod(int method)` Sets the estimation method used for estimating the ARMA parameters.
`void`	`setRelativeError(double relativeError)` Sets the stopping criterion for use in the nonlinear equation solver.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Field Detail

LEAST_SQUARES

public static final int LEAST_SQUARES

Indicates autoregressive and moving average parameters are estimated by a least-squares procedure.

See Also:: Constant Field Values

METHOD_OF_MOMENTS

public static final int METHOD_OF_MOMENTS

Indicates autoregressive and moving average parameters are estimated by a method of moments procedure.

See Also:: Constant Field Values

Constructor Detail

ARMA

public ARMA(int p,
            int q,
            double[] z)

Constructor for ARMA.

Parameters:: p - an int scalar containing the number of autoregressive (AR) parameters; q - an int scalar containing the number of moving average (MA) parameters; z - a double array containing the observations
Throws:: IllegalArgumentException - is thrown if p, q, and z.length are not consistent.

Method Detail

compute

public final void compute()
                   throws ARMA.MatrixSingularException,
                          ARMA.TooManyCallsException,
                          ARMA.IncreaseErrRelException,
                          ARMA.NewInitialGuessException,
                          ARMA.IllConditionedException,
                          ARMA.TooManyITNException,
                          ARMA.TooManyFcnEvalException,
                          ARMA.TooManyJacobianEvalException,
                          ARMA.NoProgressException

Computes least-square estimates of parameters for an ARMA model.

Throws:: ARMA.MatrixSingularException - is thrown if the input matrix is singular.; ARMA.TooManyCallsException - is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.; ARMA.IncreaseErrRelException - is thrown if the bound for the relative error is too small.; ARMA.NewInitialGuessException - is thrown if the iteration has not made good progress.; ARMA.IllConditionedException - is thrown if the problem is ill-conditioned.; ARMA.TooManyITNException - is thrown if the maximum number of iterations is exceeded.; ARMA.TooManyFcnEvalException - is thrown if the maximum number of function evaluations is exceeded.; ARMA.TooManyJacobianEvalException - is thrown if the maximum number of Jacobian evaluations is exceeded.; ARMA.NoProgressException - is thrown when the algorithm is not making any progress. Try a new initial guess.

forecast

public final double[][] forecast(int nForecast)

Computes forecasts and their associated probability limits for an ARMA model.

Parameters:: nForecast - an int scalar containing the maximum lead time for forecasts. nForecast must be greater than 0.
Returns:: a double matrix of dimensions of nForecast by backwardOrigin + 1 containing the forecasts. The forecasts are for lead times at origins z.length-backwardOrigin-1+j where . Returns NULL if the least-square estimates of parameters is not computed.

getAR

public double[] getAR()

Returns the final autoregressive parameter estimates. Note that the compute method must be invoked first before invoking this method. Otherwise, the method throws a NullPointerException exception.

Returns:: a double array of length p containing the final autoregressive parameter estimates

getAutoCovariance

public double[] getAutoCovariance()

Returns the autocovariances of the time series z. Note that the compute method must be invoked before this method. Otherwise, the method throws a NullPointerException exception.

Returns:: a double array containing the autocovariances of lag k, where k = 1, ..., p + q + 1

getBackwardOrigin

public int getBackwardOrigin()

Returns the user-specified backward origin

Returns:: an int scalar containing the user-specified backward origin

getConstant

public double getConstant()

Returns the constant parameter estimate. Note that the compute method must be invoked first before invoking this method. Otherwise, the return value is NaN.

Returns:: a double scalar containing the constant parameter estimate

getDeviations

public double[] getDeviations()

Returns the deviations used for calculating the forecast confidence limits.

Returns:: A double array of length nForecast containing the deviations for calculating forecast confidence intervals. The confidence level is specified in confidence. By default, confidence= 0.95.

getForecast

public double[] getForecast(int nForecast)

Returns forecasts

Parameters:: nForecast - An input int representing the number of requested forecasts beyond the last value in the series.
Returns:: A double array containing the nForecast+backwardOrigin forecasts. The first backwardOrigin forecasts are one-step ahead forecasts for the last backwardOrigin values in the series. The next nForecast values in the returned series are forecasts for the next values beyond the series.

getInnovationVariance

public double getInnovationVariance()

Returns the variance of the random shock.

Returns:: a double scalar equal to the variance of the random shock.

getMA

public double[] getMA()

Returns the final moving average parameter estimates. Note that the compute method must be invoked first before invoking this method. Otherwise, the method throws a NullPointerException exception.

Returns:: a double array of length q containing the final moving average parameter estimates

getMean

public double getMean()

Returns an update of the mean of the time series z. Note that the compute method must be invoked first before invoking this method. Otherwise, the return value is 0.

Returns:: a double scalar containing an update of the mean of the time series z. If the time series is not centered about its mean, and least-squares algorithm is used, zMean is not used in parameter estimation.

getNumberOfBackcasts

public int getNumberOfBackcasts()

Returns the number of backcasts used to calculate the AR coefficients for the time series z. Note that the compute method must be invoked first before invoking this method. Otherwise, the return value is 0.

Returns:: an int scalar containing the number of backcasts calculated, this value will be less than or equal to the maximum number of backcasts set in the setBackcasting method.

getParamEstimatesCovariance

public double[][] getParamEstimatesCovariance()

Returns the covariances of parameter estimates. Note that the compute method must be invoked first before invoking this method. Otherwise, the method throws a NullPointerException exception.

Returns:: a double matrix of dimensions of np by np, where np = p + q + 1 if z is centered about zMean, and np = p + q if z is not centered, containing the covariances of parameter estimates. The ordering of variables is zMean, ar, and ma.

getPsiWeights

public double[] getPsiWeights()

Returns the psi weights of the infinite order moving average form of the model. Note that the forecast method must be invoked first before invoking this method. Otherwise, the method throws a NullPointerException exception.

Returns:: a double array of length nForecast containing the psi weights of the infinite order moving average form of the model.

getResidual

public double[] getResidual()

Returns the residuals. Note that the compute method must be invoked first before invoking this method. Otherwise, the method throws a NullPointerException exception.

Returns:: a double array of length z.length - Math.max(arLags[i]) + length containing the residuals (including backcasts) at the final parameter estimate point in the first z.length - Math.max(arLags[i]) + nb, where nb is the number of values backcast, nb=ARMA.getNumberOfBackcasts(). This method is only applicable using least-squares algorithm.

getSSResidual

public double getSSResidual()

Returns the sum of squares of the random shock. Note that the compute method must be invoked first before invoking this method. Otherwise, the return value is 0.

Returns:: a double scalar containing the sum of squares of the random shock, ${rm {residual}}[0]^2 + ldots + {rm {residual}}[{rm {na - 1}}]^2$ , where residual is the array return from the getResidual method and na = residual.length. This method is only applicable using least-squares algorithm.

getVariance

public double getVariance()

Returns the variance of the time series z. Note that the compute method must be invoked first before invoking this method. Otherwise, the return value is NaN.

Returns:: a double scalar containing the variance of the time series z

setARLags

public void setARLags(int[] arLags)

Sets the order of the autoregressive parameters.

Parameters:: arLags - an int array of length p containing the order of the autoregressive parameters. The elements of arLags must be greater than or equal to 1. Default: arLags = [1, 2, ..., p]

setArmaInfo

public void setArmaInfo(double constant,
                        double[] ar,
                        double[] ma,
                        double var)

Sets the ARMA_Info Object to previously determined values

Parameters:: constant - a double scalar equal to the constant term in the ARMA model.; ar - a double array of length p containing estimates of the autoregressive parameters.; ma - a double array of length q containing estimates of the moving average parameters.; var - a double scalar equal to the innovation variance

setBackcasting

public void setBackcasting(int maxBackcast,
                           double tolerance)

Sets backcasting option.

Parameters:: maxBackcast - an int scalar containing the maximum length of backcasting and must be greater than or equal to 0. Default: maxBackcast = 10.; tolerance - a double scalar containing the tolerance level used to determine convergence of the backcast algorithm. Typically, tolerance is set to a fraction of an estimate of the standard deviation of the time series. Default: tolerance = 0.01 * standard deviation of z.

setBackwardOrigin

public void setBackwardOrigin(int backwardOrigin)

Sets the maximum backward origin.

Parameters:: backwardOrigin - an int scalar specifying the maximum backward origin. backwardOrigin must be greater than or equal to 0 and less than or equal to z.length - Math.max(maxar, maxma), where
maxar = Math.max(arLags[i]), maxma = Math.max(maLags[j]), and forecasts at origins z.length - backwardOrigin through z.length are generated. Default: backwardOrigin = 0.

setCenter

public void setCenter(boolean center)

Sets center option.

Parameters:: center - a boolean scalar. If false is specified, the time series is not centered about its mean, zMean. If true is specified, the time series is centered about its mean. Default: center = true.

setConfidence

public void setConfidence(double confidence)

Sets the confidence level for calculating confidence limit deviations returned from getDeviations.

Parameters:: confidence - a double scalar specifying the confidence level used in computing forecast confidence intervals. Typical choices for confidence are 0.90, 0.95, and 0.99. confidence must be greater than 0.0 and less than 1.0. Default: confidence = 0.95.

setConvergenceTolerance

public void setConvergenceTolerance(double convergenceTolerance)

Sets the tolerance level used to determine convergence of the nonlinear least-squares algorithm.

Parameters:: convergenceTolerance - a double scalar containing the tolerance level used to determine convergence of the nonlinear least-squares algorithm. convergenceTolerance represents the minimum relative decrease in sum of squares between two iterations required to determine convergence. Hence, convergenceTolerance must be greater than or equal to 0. The default value is ${rm {max}}(10^{-10}, {rm {eps}}^{2/3})$ , where eps = 2.2204460492503131e-16.

setInitialEstimates

public void setInitialEstimates(double[] ar,
                                double[] ma)

Sets preliminary estimates for the LEAST_SQUARES estimation method. The values of the autoregressive and moving average parameters submitted are used as intial values for least squares estimation. Otherwise they are initialized to values computed using the method of moments. When the estimation method is set to METHOD_OF_MOMENTS these initial values are not used.

Parameters:: ar - a double array of length p containing preliminary estimates of the autoregressive parameters. ar is computed internally if this method is not used. This method is only applicable using least-squares algorithm.; ma - a double array of length q containing preliminary estimates of the moving average parameters. ma is computed internally if this method is not used. This method is only applicable using least-squares algorithm.

setMALags

public void setMALags(int[] maLags)

Sets the order of the moving average parameters.

Parameters:: maLags - an int array of length q containing the order of the moving average parameters. The elements of maLags must be greater than or equal to 1. Default: maLags = [1, 2, ..., q]

setMaxIterations

public void setMaxIterations(int iterations)

Sets the maximum number of iterations.

Parameters:: iterations - an int scalar specifying the maximum number of iterations allowed in the nonlinear equation solver used in both the method of moments and least-squares algorithms. Default: interations = 200.

setMean

public void setMean(double zMean)

Sets an initial estimate of the mean of the time series z.

Parameters:: zMean - a double scalar containing an initial estimate of the mean of the time series z. If the time series is not centered about its mean, and least-squares algorithm is used, zMean is not used in parameter estimation.

setMethod

public void setMethod(int method)

Sets the estimation method used for estimating the ARMA parameters.

Parameters:: method - an int scalar specifying the method to be use. If ARMA.METHOD_OF_MOMENTS is specified, the autoregressive and moving average parameters are estimated by a method of moments procedure. If ARMA.LEAST_SQUARES is specified, the autoregressive and moving average parameters are estimated by a least-squares procedure. Default method = ARMA.METHOD_OF_MOMENTS.

setRelativeError

public void setRelativeError(double relativeError)

Sets the stopping criterion for use in the nonlinear equation solver.

Parameters:: relativeError - a double scalar containing the stopping criterion for use in the nonlinear equation solver used in both the method of moments and least-squares algorithms. Default: relativeError = 2.2204460492503131e-14.