KolmogorovTwoSample (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 6.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class KolmogorovTwoSample

java.lang.Object
  com.imsl.stat.KolmogorovTwoSample

All Implemented Interfaces:: Serializable

public class KolmogorovTwoSample
extends Object
implements Serializable
extends Object
implements Serializable

Performs a Kolmogorov-Smirnov two-sample test.

Class KolmogorovTwoSample computes Kolmogorov-Smirnov two-sample test statistics for testing that two continuous cumulative distribution functions (CDF's) are identical based upon two random samples. One- or two-sided alternatives are allowed. Exact p-values are computed for the two-sided test when , where n is the number of non-missing X observations and m the number of non-missing Y observation.

Let denote the empirical CDF in the X sample, let denote the empirical CDF in the Y sample and let the corresponding population distribution functions be denoted by and , respectively. Then, the hypotheses tested by KolmogorovTwoSample are as follows:

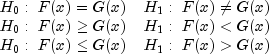
$begin{array}{ll} H_0:~ F(x) = G(x) & H_1:~F(x) ne G(x) \ H_0:~ F(x) ge G(x) & H_1:~F(x) lt G(x) \ H_0:~ F(x) le G(x) & H_1:~F(x) gt G(x) end{array}$

The test statistics are given as follows:

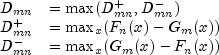
$begin{array}{rl} D_{mn} & = max(D_{mn}^{+}, D_{mn}^{-}) \ D_{mn}^{+} & = max_x(F_n(x)-G_m(x)) \ D_{mn}^{-} & = max_x(G_m(x)-F_n(x)) end{array}$

Asymptotically, the distribution of the statistic

$Z = D_{mn} sqrt{frac{m+n}{mn}}$

converges to a distribution given by Smirnov (1939).

Exact probabilities for the two-sided test are computed when , according to an algorithm given by Kim and Jennrich (1973). When , the very good approximations given by Kim and Jennrich are used to obtain the two-sided p-values. The one-sided probability is taken as one half the two-sided probability. This is a very good approximation when the p-value is small (say, less than 0.10) and not very good for large p-values.

See Also:: Example, Serialized Form

Constructor Summary
`KolmogorovTwoSample(double[] x, double[] y)` Constructs a two sample Kolmogorov-Smirnov goodness-of-fit test.

Method Summary
`double`	`getMaximumDifference()` Returns $D^{+}$ , the maximum difference between the theoretical and empirical CDF's.
`double`	`getMinimumDifference()` Returns $D^{-}$ , the minimum difference between the theoretical and empirical CDF's.
`int`	`getNumberMissingX()` Returns the number of missing values in the `x` sample.
`int`	`getNumberMissingY()` Returns the number of missing values in the `y` sample.
`double`	`getOneSidedPValue()` Probability of the statistic exceeding D under the null hypothesis of equality and against the one-sided alternative.
`double`	`getTestStatistic()` Returns $D = max(D^{+}, D^{-})$ .
`double`	`getTwoSidedPValue()` Probability of the statistic exceeding D under the null hypothesis of equality and against the two-sided alternative.
`double`	`getZ()` Returns the normalized D statistic without the continuity correction applied.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Constructor Detail

KolmogorovTwoSample

public KolmogorovTwoSample(double[] x,
                           double[] y)

Constructs a two sample Kolmogorov-Smirnov goodness-of-fit test.

Parameters:: x - is an array containing the observations from the first sample.; y - is an array containing the observations from the second sample.

Method Detail

getMaximumDifference

public double getMaximumDifference()

Returns $D^{+}$ , the maximum difference between the theoretical and empirical CDF's.

Returns:: The value $D^{+}$ .

getMinimumDifference

public double getMinimumDifference()

Returns $D^{-}$ , the minimum difference between the theoretical and empirical CDF's.

Returns:: The value $D^{-}$ .

getNumberMissingX

public int getNumberMissingX()

Returns the number of missing values in the x sample.

Returns:: The number of missing values in x.

getNumberMissingY

public int getNumberMissingY()

Returns the number of missing values in the y sample.

Returns:: The number of missing values in y.

getOneSidedPValue

public double getOneSidedPValue()

Probability of the statistic exceeding D under the null hypothesis of equality and against the one-sided alternative. An exact probability is computed if the number of observation is less than or equal to 80, otherwise an approximate probability is computed.

Returns:: the one-sided probability.

getTestStatistic

public double getTestStatistic()

Returns $D = max(D^{+}, D^{-})$ .

Returns:: The value D.

getTwoSidedPValue

public double getTwoSidedPValue()

Probability of the statistic exceeding D under the null hypothesis of equality and against the two-sided alternative. This probability is twice the probability,

, reported by getOneSidedPValue, (or 1.0 if

. This approximation is nearly exact when

Returns:: the two-sided probability.

getZ

public double getZ()

Returns the normalized D statistic without the continuity correction applied.

Returns:: the value Z