NormTwoSample (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 6.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class NormTwoSample

java.lang.Object
  com.imsl.stat.NormTwoSample

All Implemented Interfaces:: Serializable, Cloneable

public class NormTwoSample
extends Object
implements Serializable, Cloneable
extends Object
implements Serializable, Cloneable

Computes statistics for mean and variance inferences using samples from two normal populations.

Class NormTwoSample computes statistics for making inferences about the means and variances of two normal populations, using independent samples in x1 and x2. For inferences concerning parameters of a single normal population, see class NormOneSample.

Let and be the mean and variance of the first population, and let and be the corresponding quantities of the second population. The function contains test confidence intervals for difference in means, equality of variances, and the pooled variance.

The means and variances for the two samples are as follows:

$bar x_1 = left( {sum {x_{1i} /n_1 } } right), ,,,,,,,,,,,,,,,,,, bar x_2 = left( {sum {x_{2i} } } right)/n_2$

and

$s_1^2 = sum {left( {x_{1i} - bar x_1 } right)} ^2 /left( {n_1 - 1} right), ,,,,,,,,,,,s_2^2 = sum {left( {x_{2i} - {bar x}_2} right)} ^2 /left( {n_2 - 1} right)$

Inferences about the Means

The test that the difference in means equals a certain value, for example, , depends on whether or not the variances of the two populations can be considered equal. If the variances are equal and meanHypothesis equals 0, the test is the two-sample t-test, which is equivalent to an analysis-of-variance test. The pooled variance for the difference-in-means test is as follows:

$s^2 = frac{{left( {n_1 - 1} right)s_1 + left( {n_2 - 1} right)s_2 }} {{n_1 + n_2 - 2}}$

The t statistic is as follows:

$t = frac{{bar x_1 - bar x_2 - mu _0 }} {ssqrt {{left( {1/n_1 } right)} + left( {1/n_2 } right)}}$

Also, the confidence interval for the difference in means can be obtained by first assigning the unequal variances flag to false. This can be done by calling the setUnequalVariances method. The confidence interval can then be obtained by the getLowerCIDiff and getUpperCIDiff methods.

If the population variances are not equal, the ordinary t statistic does not have a t distribution and several approximate tests for the equality of means have been proposed. (See, for example, Anderson and Bancroft 1952, and Kendall and Stuart 1979.) One of the earliest tests devised for this situation is the Fisher-Behrens test, based on Fisher's concept of fiducial probability. A procedure used in the getTTest, getLowerCIDiff and getUpperCIDiff methods assuming unequal variances are specified is the Satterthwaite's procedure, as suggested by H.F. Smith and modified by F.E. Satterthwaite (Anderson and Bancroft 1952, p. 83). Use setUnequalVariances true to obtain results assuming unequal variances.

The test statistic is

$t' = left( {bar x_1 - bar x_2 - mu _0 } right)/s_d$

where

$s_d = sqrt {left( {s_1^2 /n_1 } right) + left( {s_2^2 /n_2 } right)}$

Under the null hypothesis of , this quantity has an approximate t distribution with degrees of freedom df, given by the following equation:

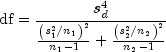
${rm{df}} = frac{{s_d^4 }}{{frac{{left( {s_1^2 /n_1 } right)^2 }}{{n_1 - 1}} + frac{{left( {s_2^2 /n_2 } right)^2 }}{{n_2 - 1}}}}$

Inferences about Variances

The F statistic for testing the equality of variances is given by $F = s_{max }^2 /s_{min }^2$ , where $s_{max}^2$ is the larger of and . If the variances are equal, this quantity has an F distribution with and degrees of freedom.

It is generally not recommended that the results of the F test be used to decide whether to use the regular t-test or the modified on a single set of data. The modified (Satterthwaite's procedure) is the more conservative approach to use if there is doubt about the equality of the variances.

See Also:: Example, Serialized Form

Constructor Summary
`NormTwoSample(double[] x, double[] y)` Constructor to compute statistics for mean and variance inferences using samples from two normal populations.

Method Summary
`void`	`downdateX(double[] x)` Removes the observations in `x` from the first sample.
`void`	`downdateY(double[] y)` Removes the observations in `y` from the second sample.
`double`	`getChiSquaredTest()` Returns the test statistic associated with the chi-squared test for common, or pooled, variances.
`int`	`getChiSquaredTestDF()` Returns the degrees of freedom associated with the chi-squared test for the common, or pooled, variances.
`double`	`getChiSquaredTestP()` Returns the probability of a larger chi-squared associated with the chi-squared test for common, or pooled, variances.
`double`	`getDiffMean()` Returns the difference in means, mean of `x` - mean of `y`.
`double`	`getFTest()` Returns the F test value of the F test for equality of variances.
`int`	`getFTestDFdenominator()` Returns the denominator degrees of freedom of the F test for equality of variances.
`int`	`getFTestDFnumerator()` Returns the numerator degrees of freedom of the F test for equality of variances.
`double`	`getFTestP()` Returns the probability of a larger F in absolute value for the F test for equality of variances, assuming equal variances.
`double`	`getLowerCICommonVariance()` Returns the lower confidence limits for the common, or pooled, variance.
`double`	`getLowerCIDiff()` Returns the lower confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set by setUnequalVariances.
`double`	`getLowerCIRatioVariance()` Returns the approximate lower confidence limit for the ratio of the variance of the first population to the second.
`double`	`getMeanX()` Returns the mean of the first sample, `x`.
`double`	`getMeanY()` Returns the mean of the second sample, `y`.
`double`	`getPooledVariance()` Returns the Pooled variance for the two samples.
`double`	`getStdDevX()` Returns the standard deviation of the first sample.
`double`	`getStdDevY()` Returns the standard deviation of the second sample.
`double`	`getTTest()` Returns the test statistic for the Satterthwaite's approximation.
`double`	`getTTestDF()` Returns the degrees of freedom for the Satterthwaite's approximation for t-test for either equal or unequal variances, depending on the value set by `setUnequalVariances`.
`double`	`getTTestP()` Returns the approximate probability of a larger `t` for the Satterthwaite's approximation for equal or unequal variances.
`double`	`getUpperCICommonVariance()` Returns the upper confidence limits for the common, or pooled, variance.
`double`	`getUpperCIDiff()` Returns the upper confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set by `setUnequalVariances`.
`double`	`getUpperCIRatioVariance()` Returns the approximate upper confidence limit for the ratio of the variance of the first population to the second.
`void`	`setChiSquaredTestNull(double varianceHypothesisValue)` Sets the null hypothesis value for the chi-squared test.
`void`	`setConfidenceMean(double confidenceMean)` Sets the confidence level (in percent) for a two-sided interval estimate of the mean of `x` - the mean of `y`, in percent.
`void`	`setConfidenceVariance(double confidenceVariance)` Sets the confidence level (in percent) for two-sided interval estimate of the variances.
`void`	`setTTestNull(double meanHypothesis)` Sets the Null hypothesis value for t-test for the mean.
`void`	`setUnequalVariances(boolean eqVar)` Specifies whether to return statistics based on equal or unequal variances.
`void`	`update(double[] x, double[] y)` Concatenates samples x and y to the samples provided in the constructor.
`void`	`updateX(double[] x)` Concatenates the values in `x` to the first sample provided in the constructor.
`void`	`updateY(double[] y)` Concatenates the values in `y` to the second sample provided in the constructor.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Constructor Detail

NormTwoSample

public NormTwoSample(double[] x,
                     double[] y)

Constructor to compute statistics for mean and variance inferences using samples from two normal populations.

Parameters:: x - is a double array containing the first sample.; y - is a double array containing the second sample.

Method Detail

downdateX

public void downdateX(double[] x)

Removes the observations in x from the first sample.

Parameters:: x - is a double array containing the values to remove from the first sample.

downdateY

public void downdateY(double[] y)

Removes the observations in y from the second sample.

Parameters:: y - is a double array containing the values to remove from the second sample.

getChiSquaredTest

public double getChiSquaredTest()

Returns the test statistic associated with the chi-squared test for common, or pooled, variances. The chi-squared test is a test of the hypothesis

where

is the null hypothesis value as described in setChiSquaredTestNull.

Returns:: a double containing the test statistic for the chi-squared test.

getChiSquaredTestDF

public int getChiSquaredTestDF()

Returns the degrees of freedom associated with the chi-squared test for the common, or pooled, variances. The chi-squared test is a test of the hypothesis

where

is the null hypothesis value as described in setChiSquaredTestNull.

Returns:: an int containing the degrees of freedom for the chi-squared test.

getChiSquaredTestP

public double getChiSquaredTestP()

Returns the probability of a larger chi-squared associated with the chi-squared test for common, or pooled, variances. The chi-squared test is a test of the hypothesis

where

is the null hypothesis value as described in setChiSquaredTestNull.

Returns:: a double containing the probability of a larger chi-squared for the chi-squared test for variances.

getDiffMean

public double getDiffMean()

Returns the difference in means, mean of x - mean of y.

Returns:: a double containing the difference in mean.

getFTest

public double getFTest()

Returns the F test value of the F test for equality of variances.

Returns:: a double containing the F test value of the F test for equality of variances.

getFTestDFdenominator

public int getFTestDFdenominator()

Returns the denominator degrees of freedom of the F test for equality of variances.

Returns:: a int containing the denominator degrees of freedom.

getFTestDFnumerator

public int getFTestDFnumerator()

Returns the numerator degrees of freedom of the F test for equality of variances.

Returns:: a int containing the numerator degrees of freedom.

getFTestP

public double getFTestP()

Returns the probability of a larger F in absolute value for the F test for equality of variances, assuming equal variances.

Returns:: a double containing the probability of a larger F in absolute value, assuming equal variances.

getLowerCICommonVariance

public double getLowerCICommonVariance()

Returns the lower confidence limits for the common, or pooled, variance.

Returns:: a double containing the lower confidence limits for the variance.

getLowerCIDiff

public double getLowerCIDiff()

Returns the lower confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set by setUnequalVariances. setUnequalVariances

Returns:: a double containing the lower confidence limit for the mean of the first sample minus the mean of the second sample.

getLowerCIRatioVariance

public double getLowerCIRatioVariance()

Returns the approximate lower confidence limit for the ratio of the variance of the first population to the second.

Returns:: a double containing the approximate lower confidence limit variance.

getMeanX

public double getMeanX()

Returns the mean of the first sample, x.

Returns:: a double containing the mean.

getMeanY

public double getMeanY()

Returns the mean of the second sample, y.

Returns:: a double containing the mean.

getPooledVariance

public double getPooledVariance()

Returns the Pooled variance for the two samples.

Returns:: a double containing the Pooled variance for the two samples.

getStdDevX

public double getStdDevX()

Returns the standard deviation of the first sample.

Returns:: a double containing the standard deviation of the first sample.

getStdDevY

public double getStdDevY()

Returns the standard deviation of the second sample.

Returns:: a double containing the standard deviation of the second sample.

getTTest

public double getTTest()

Returns the test statistic for the Satterthwaite's approximation. The value returned will be based on assumption of equal or unequal variances based on the the value set by setUnequalVariances. setUnequalVariances

Returns:: a double containing the test statistic for the t-test.

getTTestDF

public double getTTestDF()

Returns the degrees of freedom for the Satterthwaite's approximation for t-test for either equal or unequal variances, depending on the value set by setUnequalVariances. setUnequalVariances

Returns:: an double containing the degrees of freedom for the t-test.

getTTestP

public double getTTestP()

Returns the approximate probability of a larger t for the Satterthwaite's approximation for equal or unequal variances. setUnequalVariances

Returns:: a double containing the probability for the t-test.

getUpperCICommonVariance

public double getUpperCICommonVariance()

Returns the upper confidence limits for the common, or pooled, variance.

Returns:: a double containing the upper confidence limits for the variance.

getUpperCIDiff

public double getUpperCIDiff()

Returns the upper confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set by setUnequalVariances. setUnequalVariances

Returns:: a double containing the upper confidence limit for the mean of the first sample minus the mean of the second sample.

getUpperCIRatioVariance

public double getUpperCIRatioVariance()

Returns the approximate upper confidence limit for the ratio of the variance of the first population to the second.

Returns:: a double containing the approximate upper confidence limit variance.

setChiSquaredTestNull

public void setChiSquaredTestNull(double varianceHypothesisValue)

Sets the null hypothesis value for the chi-squared test. The default is 1.0.

Parameters:: varianceHypothesisValue - a double containing the null hypothesis value for the chi-squared test.

setConfidenceMean

public void setConfidenceMean(double confidenceMean)

Sets the confidence level (in percent) for a two-sided interval estimate of the mean of x - the mean of y, in percent. Argument confidenceMean must be between 0.0 and 1.0 and is often 0.90, 0.95 or 0.99. For a one-sided confidence interval with confidence level c (at least 50 percent), set

. If the confidence mean is not specified, a 95-percent confidence interval is computed. Default: confidenceMean = .95

Parameters:: confidenceMean - double containing the confidence level of the mean.

setConfidenceVariance

public void setConfidenceVariance(double confidenceVariance)

Sets the confidence level (in percent) for two-sided interval estimate of the variances. Under the assumption of equal variances, the pooled variance is used to obtain a two-sided confidenceVariance percent confidence interval for the common variance with getLowerCICommonVariance or getUpperCICommonVariance. Without making the assumption of equal variances, setUnequalVariances , the ratio of the variances is of interest. A two-sided confidenceVariance percent confidence interval for the ratio of the variance of the first sample to that of the second sample is given by the getLowerCIRatioVariance and getUpperCIRatioVariance. See setUnequalVariances and getUpperCIRatioVariance. The confidence intervals are symmetric in probability. Argument confidenceVariance must be between 0.0 and 1.0 and is often 0.90, 0.95 or 0.99. The default is 0.95.

Parameters:: confidenceVariance - double containing the confidence level of the variance.

setTTestNull

public void setTTestNull(double meanHypothesis)

Sets the Null hypothesis value for t-test for the mean. meanHypothesis=0.0 by default.

Parameters:: meanHypothesis - double containing the hypothesis value.

setUnequalVariances

public void setUnequalVariances(boolean eqVar)

Specifies whether to return statistics based on equal or unequal variances. The default is to return statistics for equal variances. if eqVar is True then statistics for unequal variances will be returned.

Parameters:: eqVar - a boolean containing a true or false value. A value of true will cause results for unequal variances to be returned. A value of false will cause results for equal variances to be returned.

update

public void update(double[] x,
                   double[] y)

Concatenates samples x and y to the samples provided in the constructor.

Parameters:: x - is a double array containing updates to the first sample.; y - is a double array containing updates to the second sample.

updateX

public void updateX(double[] x)

Concatenates the values in x to the first sample provided in the constructor.

Parameters:: x - is a double array containing updates for the first sample.

updateY

public void updateY(double[] y)

Concatenates the values in y to the second sample provided in the constructor.

Parameters:: y - is a double array containing updates for the second sample.

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 6.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat Class NormTwoSample

NormTwoSample

downdateX

downdateY

getChiSquaredTest

getChiSquaredTestDF

getChiSquaredTestP

getDiffMean

getFTest

getFTestDFdenominator

getFTestDFnumerator

getFTestP

getLowerCICommonVariance

getLowerCIDiff

getLowerCIRatioVariance

getMeanX

getMeanY

getPooledVariance

getStdDevX

getStdDevY

getTTest

getTTestDF

getTTestP

getUpperCICommonVariance

getUpperCIDiff

getUpperCIRatioVariance

setChiSquaredTestNull

setConfidenceMean

setConfidenceVariance

setTTestNull

setUnequalVariances

update

updateX

updateY

com.imsl.stat
Class NormTwoSample