com.imsl.datamining

Class KohonenSOM

java.lang.Object

com.imsl.datamining.KohonenSOM

All Implemented Interfaces:

Serializable, Cloneable

public class KohonenSOM
extends Object
implements Serializable, Cloneable

A Kohonen self organizing map.

A self-organizing map (SOM), also known as a Kohonen map or Kohonen SOM, is a technique for gathering high-dimensional data into clusters that are constrained to lie in low dimensional space, usually two dimensions. A Kohonen map is a widely used technique for the purpose of feature extraction and visualization for very high dimensional data in situations where classifications are not known beforehand. The Kohonen SOM is equivalent to an artificial neural network having inputs linked to every node in the network. Self-organizing maps use a neighborhood function to preserve the topological properties of the input space.

In a Kohonen map, nodes are arranged in a rectangular or hexagonal grid or lattice. The input is connected to each node, and the output of the Kohonen map is the zero-based (i, j) index of the node that is closest to the input. A Kohonen map involves two steps: training and forecasting. Training builds the map using input examples (vectors), and forecasting classifies a new input.

During training, an input vector is fed to the network. The input's Euclidean distance from all the nodes is calculated. The node with the shortest distance is identified and is called the Best Matching Unit, or BMU. After identifying the BMU, the weights of the BMU and the nodes closest to it in the SOM lattice are updated towards the input vector. The magnitude of the update decreases with time and with distance (within the lattice) from the BMU. The weights of the nodes surrounding the BMU are updated according to:

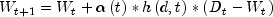
where 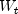represents the node weights, 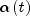is the monotonically decreasing learning coefficient function, 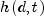is the neighborhood function, d is the lattice distance between the node and the BMU, and 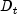is the input vector.

The monotonically decreasing learning coefficient function 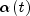is a scalar factor that defines the size of the update correction. The value of 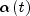decreases with the step index t.

The neighborhood function 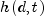depends on the lattice distance d between the node and the BMU, and represents the strength of the coupling between the node and BMU. In the simplest form, the value of 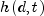is 1 for all nodes closest to the BMU and 0 for others, but a Gaussian function is also commonly used. Regardless of the functional form, the neighborhood function shrinks with time (Hollmén, 15.2.1996). Early on, when the neighborhood is broad, the self-organizing takes place on the global scale. When the neighborhood has shrunk to just a couple of nodes, the weights converge to local estimates.

Note that in a rectangular grid, the BMU has four closest nodes for the Von Neumann neighborhood type, or eight closest nodes for the Moore neighborhood type. In a hexagonal grid, the BMU has six closest nodes.

During training, this process is repeated for a number of iterations on all input vectors.

During forecasting, the node with the shortest Euclidean distance is the winning node, and its (i, j) index is the output.

See Also:

Example, Serialized Form

Field Summary

Fields

Modifier and Type	Field and Description
static int	GRID_HEXAGONAL Indicates a hexagonal grid.
static int	GRID_RECTANGULAR Indicates a rectangular grid.
static int	TYPE_MOORE Indicates a Moore neighborhood type.
static int	TYPE_VON_NEUMANN Indicates a Von Neumann neighborhood type.

Constructor Summary

Constructors

Constructor and Description
KohonenSOM(int dim, int nrow, int ncol) Constructor for a KohonenSOM object.

Method Summary

Methods

Modifier and Type	Method and Description
int[]	forecast(double[] input) Returns a forecast computed using the KohonenSOM object.
int[][]	forecast(double[][] input) Returns forecasts computed using the KohonenSOM object.
int	getDimension() Returns the number of weights for each node.
int	getGridType() Returns the grid type.
int	getNeighborhoodType() Returns the neighborhood type for the rectangular grid.
int	getNumberOfColumns() Returns the number of columns of the node grid.
int	getNumberOfRows() Returns the number of rows of the node grid.
double[][][]	getWeights() Returns the weights of the nodes.
double[]	getWeights(int i, int j) Returns the weights of the node at (i, j) in the node grid.
boolean	isWrapAround() Returns whether the opposite edges are connected or not.
void	setGridType(int type) Sets the grid type.
void	setNeighborhoodType(int type) Sets the neighborhood type.
void	setWeights() Sets the weights of the nodes using random numbers.
void	setWeights(double[][][] weights) Sets the weights of the nodes.
void	setWeights(int i, int j, double[] weights) Sets the weights of the node at (i, j) in the node grid.
void	setWeights(Random random) Sets the weights of the nodes using a Random object.
void	wrapAround() Sets a flag to indicate the map should wrap around or connect opposite edges.

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Field Detail

GRID_HEXAGONAL

public static final int GRID_HEXAGONAL

Indicates a hexagonal grid.

See Also:

Constant Field Values

GRID_RECTANGULAR

public static final int GRID_RECTANGULAR

Indicates a rectangular grid.

See Also:

Constant Field Values

TYPE_MOORE

public static final int TYPE_MOORE

Indicates a Moore neighborhood type.

See Also:

Constant Field Values

TYPE_VON_NEUMANN

public static final int TYPE_VON_NEUMANN

Indicates a Von Neumann neighborhood type.

See Also:

Constant Field Values

Constructor Detail

KohonenSOM

public KohonenSOM(int dim,
          int nrow,
          int ncol)

Constructor for a KohonenSOM object.

Parameters:

dim - An int scalar containing the number of weights for each node in the node grid. dim must be greater than zero.

nrow - An int scalar containing the number of rows in the node grid. nrow must be greater than zero.

ncol - An int scalar containing the number of columns in the node grid. ncol must be greater than zero.

Method Detail

forecast

public int[] forecast(double[] input)

Returns a forecast computed using the KohonenSOM object.

Parameters:

input - A double array containing the input data. input.length must be equal to dim.

Returns:

An int array of length 2 containing the (i, j) index of the output node.

forecast

public int[][] forecast(double[][] input)

Returns forecasts computed using the KohonenSOM object.

Parameters:

input - A double matrix containing input.length observations of data. input[i].length must be equal to dim.

Returns:

An int matrix containing the output indices of the nodes. The i-th row contains the (i, j) index of the output node for input[i].

getDimension

public int getDimension()

Returns the number of weights for each node.

Returns:

An int scalar containing the number of weights for each node.

getGridType

public int getGridType()

Returns the grid type.

Returns:

An int scalar containing the grid type. The return value is either KohonenSOM.GRID_RECTANGULAR or KohonenSOM.GRID_HEXAGONAL

getNeighborhoodType

public int getNeighborhoodType()

Returns the neighborhood type for the rectangular grid.

Returns:

An int scalar containing the neighborhood type. The return value is either KohonenSOM.TYPE_VON_NEUMANN or KohonenSOM.TYPE_MOORE

getNumberOfColumns

public int getNumberOfColumns()

Returns the number of columns of the node grid.

Returns:

An int scalar containing the number of columns of the node grid.

getNumberOfRows

public int getNumberOfRows()

Returns the number of rows of the node grid.

Returns:

An int scalar containing the number of rows of the node grid.

getWeights

public double[][][] getWeights()

Returns the weights of the nodes.

Returns:

An nrow by ncol matrix of double arrays containing the weights of the nodes.

getWeights

public double[] getWeights(int i,
                  int j)

Returns the weights of the node at (i, j) in the node grid.

Parameters:

i - An int scalar containing the row index of the node in the node grid, where .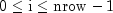

j - An int scalar containing the column index of the node in the node grid, where .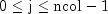

Returns:

A double array containing the weights of the node at (i, j) in the node grid.

isWrapAround

public boolean isWrapAround()

Returns whether the opposite edges are connected or not.

Returns:

A boolean indicating whether or not the opposite edges are connected. It is true if the opposite edges are connected. Otherwise, it is false.

setGridType

public void setGridType(int type)

Sets the grid type.

Parameters:

type - An int scalar containing the grid type, rectangular (KohonenSOM.GRID_RECTANGULAR) or hexagonal (KohonenSOM.GRID_HEXAGONAL).

Default: type = GRID_RECTANGULAR.

type	Description
GRID_RECTANGULAR	Use a rectangular grid (type = 0).
GRID_HEXAGONAL	Use a hexagonal grid (type = 1).

setNeighborhoodType

public void setNeighborhoodType(int type)

Sets the neighborhood type.

Parameters:

type - An int scalar containing the neighborhood type, Von Neumann (KohonenSOM.TYPE_VON_NEUMANN) or Moore (KohonenSOM.TYPE_MOORE). This method is ignored for a hexagonal grid.

Default: type = TYPE_VON_NEUMANN.

type	Description
TYPE_VON_NEUMANN	Use the Von Neumann (type = 0) neighborhood type.
TYPE_MOORE	Use the Moore (type = 1) neighborhood type.

setWeights

public void setWeights()

Sets the weights of the nodes using random numbers. The weights are in [0.0, 1.0].

setWeights

public void setWeights(double[][][] weights)

Sets the weights of the nodes.

Parameters:

weights - An nrow by ncol matrix of double arrays containing the weights of the nodes. weights[i][j].length must be equal to dim.

setWeights

public void setWeights(int i,
              int j,
              double[] weights)

Sets the weights of the node at (i, j) in the node grid.

Parameters:

i - An int scalar containing the row index of the node in the node grid, where .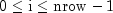

j - An int scalar containing the column index of the node in the node grid, where .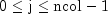

weights - A double array containing the weights. weights.length must be equal to dim.

setWeights

public void setWeights(Random random)

Sets the weights of the nodes using a Random object. The weights are generated using the Random.nextDouble method.

Parameters:

random - A Random object used to generate random numbers for the nodes.

wrapAround

public void wrapAround()

Sets a flag to indicate the map should wrap around or connect opposite edges. A hexagonal grid must have an even number of rows to wrap around. By default, opposite edges are not connected.