AutoCorrelation (JMSL Numerical Library)

java.lang.Object
- com.imsl.stat.AutoCorrelation

All Implemented Interfaces:

Serializable, Cloneable
```
public class AutoCorrelation
extends Object
implements Serializable, Cloneable
```
Computes the sample autocorrelation function of a stationary time series.
AutoCorrelation estimates the autocorrelation function of a stationary time series given a sample of n observations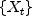 ${X_t}$ for .

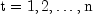Let
be the estimate of the mean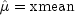 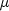of the time series 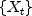${X_t}$ where

$hat mu = left{pa begin{array}{ll} mu & {rm for};mu; {rm known} \ frac{1}{n}sumlimits_{t=1}^n {X_t } & {rm for};mu; {rm unknown} end{array} right.$
The autocovariance function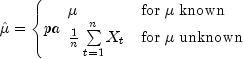 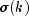is estimated by
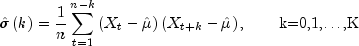
$hat sigma left( k right) = frac{1}{n} sumlimits_{t = 1}^{n - k} {left( {X_t - hat mu } right)} left( {X_{t + k} - hat mu } right), mbox{hspace{20pt}k=0,1,dots,K}$

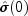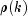where K = maximum_lag. Note that is an estimate of the sample variance. The autocorrelation function is estimated by
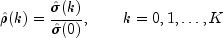
$hatrho(k) = frac{hat sigma(k)}{hat sigma(0)},mbox{hspace{20pt}} k=0,1,dots,K$

Note that 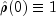by definition.

The standard errors of sample autocorrelations may be optionally computed according to the getStandardErrors method argument stderrMethod. One method (Bartlett 1946) is based on a general asymptotic expression for the variance of the sample autocorrelation coefficient of a stationary time series with independent, identically distributed normal errors. The theoretical formula is
$mbox{var}{hat rho(k)} = frac{1}{n}sumlimits_{i=-infty}^{infty} left[{rho^2(i)}+rho(i-k)rho(i+k)-4rho(i) rho(k)rho(i-k)+2rho^2(i)rho^2(k)right]$

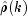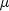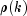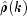where assumes is unknown. For computational purposes, the autocorrelations are replaced by their estimates for 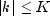, and the limits of summation are bounded because of the assumption that 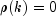for all 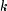such that .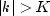

A second method (Moran 1947) utilizes an exact formula for the variance of the sample autocorrelation coefficient of a random process with independent, identically distributed normal errors. The theoretical formula is

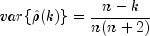
$var{hat rho(k)} = frac{n-k}{n(n+2)}$

where 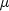is assumed to be equal to zero. Note that this formula does not depend on the autocorrelation function.
The method getPartialAutoCorrelations estimates the partial autocorrelations of the stationary time series given K = maximum_lag sample autocorrelations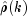 for k=0,1,...,K. Consider the AR(k) process defined by
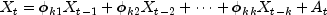
$X_t = {phi_{k1}}X_{t-1}+{phi_{k2}}X_{t-2}+ dots+{phi_{kk}}X_{t-k}+A_t$
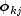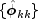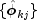where $phi_{kj}$ denotes the j-th coefficient in the process. The set of estimates ${{hat phi_{kk}}}$ for k = 1, ..., K is the sample partial autocorrelation function. The autoregressive parameters ${hat phi_{kj}}$ for j = 1, ..., k are approximated by Yule-Walker estimates for successive AR(k) models where k = 1, ..., K. Based on the sample Yule-Walker equations
$hatrho(j) = {hatphi_{k1}}hatrho(j-1) + {hatphi_{k2}}hatrho(j-2) + dots + {hatphi_{kk}}hatrho(j-k), mbox{hspace{20pt}j = 1,2,dots,k}$
a recursive relationship for k=1, ..., K was developed by Durbin (1960). The equations are given by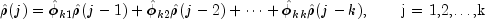

$hat phi_{kk} = left{ begin{array}{ll} hatrho(1) & {rm for};{rm k}; {rm = 1} \ frac{hatrho(k); - sumlimits_{j=1}^{k-1} {hatphi_{k-1,j}hatrho(k-j) }} {1;-; sumlimits_{j=1}^{k-1}{hatphi_{k-1,j}hatrho(j)} } & {rm for};{rm k = 2,};dots; {rm ,K} end{array} right.$
and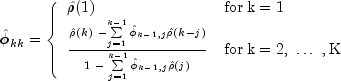
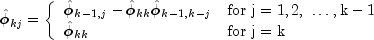
$hat phi_{kj} = left{ begin{array}{ll} hatphi_{k-1,j}-hatphi_{kk}hatphi_{k-1,k-j} & {rm for};{rm j}; {rm = 1,2,}; dots {rm,k-1} \ hat phi_{kk} & {rm for};{rm j = k} end{array} right.$

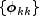This procedure is sensitive to rounding error and should not be used if the parameters are near the nonstationarity boundary. A possible alternative would be to estimate ${{phi_{kk}}}$ for successive AR(k) models using least or maximum likelihood. Based on the hypothesis that the true process is AR(p), Box and Jenkins (1976, page 65) note

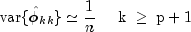
${rm var}{{ hatphi_{kk}}} simeq frac {1}{n} ;;;;; {rm k}; geq ; {rm p + 1}$

See Box and Jenkins (1976, pages 82-84) for more information concerning the partial autocorrelation function.

See Also:
Example, Serialized Form

Nested Class Summary

Nested Classes
Modifier and Type Class and Description

static class AutoCorrelation.NonPosVariancesException
The problem is ill-conditioned.

Nested Classes
Modifier and Type	Class and Description
`static class`	`AutoCorrelation.NonPosVariancesException` The problem is ill-conditioned.

Field Summary

Fields
Modifier and Type	Field and Description
`static int`	`BARTLETTS_FORMULA` Indicates standard error computation using Bartlett's formula.
`static int`	`MORANS_FORMULA` Indicates standard error computation using Moran's formula.

Constructor Summary

Constructors
Constructor and Description
`AutoCorrelation(double[] x, int maximum_lag)` Constructor to compute the sample autocorrelation function of a stationary time series.

Method Summary

Methods
Modifier and Type	Method and Description
`double[]`	`getAutoCorrelations()` Returns the autocorrelations of the time series `x`.
`double[]`	`getAutoCovariances()` Returns the variance and autocovariances of the time series `x`.
`double`	`getMean()` Returns the mean of the time series `x`.
`int`	`getNumberOfThreads()` Returns the number of `java.lang.Thread` instances used for parallel processing.
`double[]`	`getPartialAutoCorrelations()` Returns the sample partial autocorrelation function of the stationary time series `x`.
`double[]`	`getStandardErrors(int stderrMethod)` Returns the standard errors of the autocorrelations of the time series `x`.
`double`	`getVariance()` Returns the variance of the time series `x`.
`void`	`setMean(double mean)` Estimate mean of the time series `x`.
`void`	`setNumberOfThreads(int numberOfThreads)` Sets the number of `java.lang.Thread` instances to be used for parallel processing.

Methods inherited from class java.lang.Object
clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

- Field Detail
  - BARTLETTS_FORMULA
```
public static final int BARTLETTS_FORMULA
```
    Indicates standard error computation using Bartlett's formula.
    
    See Also:
    Constant Field Values
  - MORANS_FORMULA
```
public static final int MORANS_FORMULA
```
    Indicates standard error computation using Moran's formula.
    
    See Also:
    Constant Field Values
- Constructor Detail
  - AutoCorrelation
```
public AutoCorrelation(double[] x,
               int maximum_lag)
```
    Constructor to compute the sample autocorrelation function of a stationary time series.
    
    Parameters:
    x - a one-dimensional double array containing the stationary time series
    maximum_lag - an int containing the maximum lag of autocovariance, autocorrelations, and standard errors of autocorrelations to be computed. maximum_lag must be greater than or equal to 1 and less than the number of observations in x
- Method Detail
  - getAutoCorrelations
```
public double[] getAutoCorrelations()
```
    Returns the autocorrelations of the time series x.
    
    Returns:
    a double array of length maximum_lag +1 containing the autocorrelations of the time series x. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag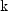 where k = 1, ..., maximum_lag.
  - getAutoCovariances
```
public double[] getAutoCovariances()
                            throws AutoCorrelation.NonPosVariancesException
```
    Returns the variance and autocovariances of the time series x.
    
    Returns:
    a double array of length maximum_lag +1 containing the variances and autocovariances of the time series x. The 0-th element of the array contains the variance of the time series x. The k-th element contains the autocovariance of lag k where k = 1, ..., maximum_lag.
    
    Throws:
    
    AutoCorrelation.NonPosVariancesException - is thrown if the problem is ill-conditioned
  - getMean
```
public double getMean()
```
    Returns the mean of the time series x.
    
    Returns:
    a double containing the mean
  - getNumberOfThreads
```
public int getNumberOfThreads()
```
    Returns the number of java.lang.Thread instances used for parallel processing.
    
    Returns:
    an int containing the number of java.lang.Thread instances used for parallel processing.
  - getPartialAutoCorrelations
```
public double[] getPartialAutoCorrelations()
```
    Returns the sample partial autocorrelation function of the stationary time series x.
    
    Returns:
    a double array of length maximum_lag containing the partial autocorrelations of the time series x.
  - getStandardErrors
```
public double[] getStandardErrors(int stderrMethod)
```
    Returns the standard errors of the autocorrelations of the time series x. Method of computation for standard errors of the autocorrelation is chosen by the stderrMethod parameter. If stderrMethod is set to BARTLETTS_FORMULA, Bartlett's formula is used to compute the standard errors of autocorrelations. If stderrMethod is set to MORANS_FORMULA, Moran's formula is used to compute the standard errors of autocorrelations.
    
    Parameters:
    stderrMethod - an int specifying the method to compute the standard errors of autocorrelations of the time series x
    
    Returns:
    a double array of length maximum_lag containing the standard errors of the autocorrelations of the time series x
  - getVariance
```
public double getVariance()
```
    Returns the variance of the time series x.
    
    Returns:
    a double containing the variance of the time series x
  - setMean
```
public void setMean(double mean)
```
    Estimate mean of the time series x.
    
    Parameters:
    mean - a double containing the estimate mean of the time series x.
  - setNumberOfThreads
```
public void setNumberOfThreads(int numberOfThreads)
```
    Sets the number of java.lang.Thread instances to be used for parallel processing.
    
    Parameters:
    numberOfThreads - an int specifying the number of java.lang.Thread instances to be used for parallel processing.
    Default: numberOfThreads = 1.

Class AutoCorrelation

Nested Class Summary

Field Summary

Constructor Summary

Method Summary

Methods inherited from class java.lang.Object

Field Detail

BARTLETTS_FORMULA

MORANS_FORMULA

Constructor Detail

AutoCorrelation

Method Detail

getAutoCorrelations

getAutoCovariances

getMean

getNumberOfThreads

getPartialAutoCorrelations

getStandardErrors

getVariance

setMean

setNumberOfThreads