- java.lang.Object
-
- com.imsl.stat.VectorAutoregression
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class VectorAutoregression extends Object implements Serializable, Cloneable
Performs vector autoregression for a multivariate time series.This class contains methods for modeling multivariate time series of the form
where each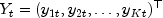
is a real-valued time series indexed by t. Define the K dimensional mean process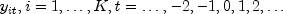
and the cross-covariance matrix![mu_t=E[Y_t]=(E[y_{1t}],ldots,E[y_{Kt}])^top](eqn_2003.png)
where for each (t,h),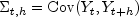
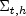 is a K * K
real-valued matrix whose (i,j)t,h element is the
covariance between
is a K * K
real-valued matrix whose (i,j)t,h element is the
covariance between 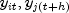 :
:
![text{Cov}(y_{it},y_{j(t+h)})=
E[(y_{it}-mu_{it})(y_{j(t+h)}-mu_{j(t+h)})].](eqn_2007.png)
The vector autoregressive model, or VAR, has a number of equivalent forms. A general form is
where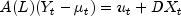
is a p-th degree matrix polynomial in the lag or backshift operator, L. Note that p is the specified autoregressive lag and ut is the error process. The error process is assumed to be a K dimensional white noise series, with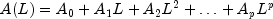
![E[u_t]=0](eqn_2010.png) and nonsingular covariance matrix,
and nonsingular covariance matrix,
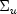 , which is constant over time. The coefficient
matrices
, which is constant over time. The coefficient
matrices 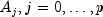 are
K * K matrices containing the coefficients of the model.
The matrix
Xt represents a matrix of deterministic terms such as trend
or seasonal variables, and D represents the associated coefficient
matrix of Xt.
are
K * K matrices containing the coefficients of the model.
The matrix
Xt represents a matrix of deterministic terms such as trend
or seasonal variables, and D represents the associated coefficient
matrix of Xt.
- See Also:
- Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description VectorAutoregression(TimeSeries ts)Constructor for the class.
-
Method Summary
Methods Modifier and Type Method and Description double[]getARConstants()Returns the current settings of the constants used in the autoregression model.int[]getARModel()Returns the autoregressive model configuration.double[][]getEstimates()Returns the parameter estimates (coefficients) of the vector autoregression model.double[][]getForecasts()Returns the h-step ahead forecast at times t=nT, nT+1, ..., T, where h=1,2, ...,maxStepsAhead.booleanisA0Flag()Returns the state ofA0Flag.voidsetA0Flag(boolean A0Flag)Sets the flag to include the leading autoregressive coefficient matrix in the model.voidsetARConstants(double[] arConstants)Sets the constants for the autoregressive model.voidsetARLag(int arLag)Sets the autoregressive lag parameter.voidsetARModel(int[] arModel)Sets the form of the autoregressive terms of the model.voidsetCenter(boolean center)Sets the flag to center the data.voidsetMaxLag(int maxLag)Sets the maximum lag.voidsetScale(boolean scale)Sets the flag to scale the data.voidsetTrend(boolean trend)Sets the flag to fit a trend parameter in the model.
-
-
-
Constructor Detail
-
VectorAutoregression
public VectorAutoregression(TimeSeries ts)
Constructor for the class.- Parameters:
ts- aTimeSeriesobject.
-
-
Method Detail
-
getARConstants
public double[] getARConstants()
Returns the current settings of the constants used in the autoregression model.- Returns:
- a
doublearray containing the constants used in the autoregression model. If the value isnull, the default values are active.
-
getARModel
public int[] getARModel()
Returns the autoregressive model configuration.- Returns:
- an
intarray specifying the autoregressive configuration. Ifnull, then all parameters are active in the current model.
-
getEstimates
public double[][] getEstimates()
Returns the parameter estimates (coefficients) of the vector autoregression model.- Returns:
- a
doublearray containing the estimated parameters (coefficients).
-
getForecasts
public double[][] getForecasts()
Returns the h-step ahead forecast at times t=nT, nT+1, ..., T, where h=1,2, ...,maxStepsAhead.The h-step ahead forecast
uses the conditional expectation of![hat{Y}_{t+h} = E[Y_{t+h}|Y_s, 0 le s le t]](eqn_2027.png)
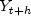 given the historical information known at time t. The estimated
VAR model approximates the conditional expectation and the forecasts are
generated from the estimated VAR model via the following recursion:
given the historical information known at time t. The estimated
VAR model approximates the conditional expectation and the forecasts are
generated from the estimated VAR model via the following recursion:
where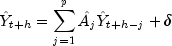
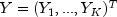 is the vector
time series and
is the vector
time series and
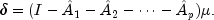
- Returns:
- a
doublematrix T-nT bymaxStepsAhead* K containing the forecasts.Note that the forecast
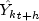 is stored in location
[t-nT][(h-1)*K + k] of the returned forecast matrix.
is stored in location
[t-nT][(h-1)*K + k] of the returned forecast matrix.
-
isA0Flag
public boolean isA0Flag()
Returns the state ofA0Flag.- Returns:
- a
booleanwhich specifies whether or not the leading coefficient matrix is nontrivial.
-
setA0Flag
public void setA0Flag(boolean A0Flag)
Sets the flag to include the leading autoregressive coefficient matrix in the model.When
true, a nontrivial, lower-triangular leading autoregressive coefficient matrix, A0, will be estimated in the model. Whenfalse, A0 is the constant identity matrix, which is also the default case.- Parameters:
A0Flag-booleanindicating whether to fit the leading coefficient matrix.Default:
A0Flag=false.
-
setARConstants
public void setARConstants(double[] arConstants)
Sets the constants for the autoregressive model. See discussion insetARModel(int[])for details.- Parameters:
arConstants- adoublearray specifying the autoregressive model constants.The input array
Default:arConstantsmust be of length (A0Flag+arLag)*K*K, such that for indices 1=0,...,(A0Flag+arLag), i=0,...,K-1, and j=0,...,K-1,arConstants[l*K*K +i*K + j]specifies a constant value for parameter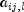 .
.
arConstants[i]=0.
-
setARLag
public void setARLag(int arLag)
Sets the autoregressive lag parameter. It must be nonnegative and less thanmaxLag.- Parameters:
arLag- anintspecifying the desired lag for the autoregressive terms. Default:arLag=1.
-
setARModel
public void setARModel(int[] arModel)
Sets the form of the autoregressive terms of the model.Without loss of generality, assume that the series mean is 0 and that there are no deterministic terms. Then we can write the vector autoregression model of lag p as
Each of the matrices Aj represents K * K unknown coefficients. In practice, many of the (p+ 1) * K * K coefficients are restricted to be 0 or otherwise constant. The leading coefficient matrix A0 must be lower-triangular and is very often equal to the identity matrix (this is the default behavior). Fully expanded the model looks like K equations in K(p+1) unknowns.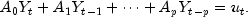
Consider each coefficient matrix as the vector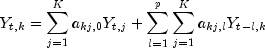
for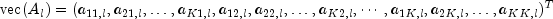
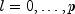 .
.
is just the columns of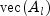
appended to each other. To specify a configuration different from the default, append the vectorized coefficient matrices as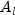
or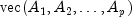
when including a nontrivial leading coefficient matrix. Set the value at index l*K*K + j*K + i to 1 or -1 to fit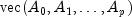
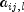 or
or 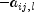 in the model. Set the value to 0 to exclude
in the model. Set the value to 0 to exclude 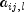 as a parameter. Note that for the leading coefficient matrix,l= 0,
the value at j*K + i is ignored unless
i is at least j, i.e., only the lower triangle of
A0 can be nontrivial.
as a parameter. Note that for the leading coefficient matrix,l= 0,
the value at j*K + i is ignored unless
i is at least j, i.e., only the lower triangle of
A0 can be nontrivial.
- Parameters:
arModel- anintarray specifying the autoregressive model parameters.For indices l=0,...,(
A0Flag+arLag), i=0,...,K-1, and j=0,...,K-1,arModel[l*K*K +i*K + j]= {-1,1} indicates that the coefficient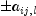 is a parameter (to be estimated) in the model.
is a parameter (to be estimated) in the model.
Default: A0 is the identity matrix and
arModel[i]=1 for all i.
-
setCenter
public void setCenter(boolean center)
Sets the flag to center the data. Ifcenter=true, column means are subtracted from the data.- Parameters:
center- abooleanindicating whether or not column means should be subtracted from the data.Default:
center=false.
-
setMaxLag
public void setMaxLag(int maxLag)
Sets the maximum lag.- Parameters:
maxLag- anintspecifying the maximum lag to consider in the first (pure VAR) stage regression.
-
setScale
public void setScale(boolean scale)
Sets the flag to scale the data.If
scale=true, the data values are mean-centered and then divided by the standard deviation.- Parameters:
scale- abooleanDefault:
scale=false.
-
setTrend
public void setTrend(boolean trend)
Sets the flag to fit a trend parameter in the model. Set totrueto include a deterministic trend in the model.- Parameters:
trend- abooleanspecifying whether or not to include a deterministic trend.Default:
trend=false.
-
-