- java.lang.Object
-
- com.imsl.finance.Finance
-
public class Finance extends Object
Collection of finance functions.
-
-
Field Summary
Fields Modifier and Type Field and Description static intAT_BEGINNING_OF_PERIODFlag used to indicate that payment is made at the beginning of each period.static intAT_END_OF_PERIODFlag used to indicate that payment is made at the end of each period.
-
Method Summary
Methods Modifier and Type Method and Description static doublecumipmt(double rate, int nper, double pv, int start, int end, int when)Returns the cumulative interest paid between two periods.static doublecumprinc(double rate, int nper, double pv, int start, int end, int when)Returns the cumulative principal paid between two periods.static doubledb(double cost, double salvage, int life, int period, int month)Returns the depreciation of an asset using the fixed-declining balance method.static doubleddb(double cost, double salvage, int life, int period, double factor)Returns the depreciation of an asset using the double-declining balance method.static doubledollarde(double fractionalDollar, int fraction)Converts a fractional price to a decimal price.static doubledollarfr(double decimalDollar, int fraction)Converts a decimal price to a fractional price.static doubleeffect(double nominalRate, int nper)Returns the effective annual interest rate.static doublefv(double rate, int nper, double pmt, double pv, int when)Returns the future value of an investment.static doublefvschedule(double principal, double[] schedule)Returns the future value of an initial principal taking into consideration a schedule of compound interest rates.static doubleipmt(double rate, int period, int nper, double pv, double fv, int when)Returns the interest payment for an investment for a given period.static doubleirr(double[] pmt)Returns the internal rate of return for a schedule of cash flows.static doubleirr(double[] pmt, double guess)Returns the internal rate of return for a schedule of cash flows.static doublemirr(double[] value, double financeRate, double reinvestRate)Returns the modified internal rate of return for a schedule of periodic cash flows.static doublenominal(double effectiveRate, int nper)Returns the nominal annual interest rate.static doublenper(double rate, double pmt, double pv, double fv, int when)Returns the number of periods for an investment for which periodic, and constant payments are made and the interest rate is constant.static doublenpv(double rate, double[] value)Returns the net present value of a stream of equal periodic cash flows, which are subject to a given discount rate.static doublepmt(double rate, int nper, double pv, double fv, int when)Returns the periodic payment for an investment.static doubleppmt(double rate, int period, int nper, double pv, double fv, int when)Returns the payment on the principal for a specified period.static doublepv(double rate, int nper, double pmt, double fv, int when)Returns the net present value of a stream of equal periodic cash flows, which are subject to a given discount rate.static doublerate(int nper, double pmt, double pv, double fv, int when)Returns the interest rate per period of an annuity.static doublerate(int nper, double pmt, double pv, double fv, int when, double guess)Returns the interest rate per period of an annuity with an initial guess.static doublesln(double cost, double salvage, int life)Returns the depreciation of an asset using the straight line method.static doublesyd(double cost, double salvage, int life, int per)Returns the depreciation of an asset using the sum-of-years digits method.static doublevdb(double cost, double salvage, int life, int start, int end, double factor, boolean no_sl)Returns the depreciation of an asset for any given period using the variable-declining balance method.static doublexirr(double[] pmt, Date[] dates)Returns the internal rate of return for a schedule of cash flows.static doublexirr(double[] pmt, Date[] dates, double guess)Returns the internal rate of return for a schedule of cash flows with a user supplied initial guess.static doublexnpv(double rate, double[] value, Date[] dates)Returns the present value for a schedule of cash flows.
-
-
-
Field Detail
-
AT_BEGINNING_OF_PERIOD
public static final int AT_BEGINNING_OF_PERIOD
Flag used to indicate that payment is made at the beginning of each period.- See Also:
- Constant Field Values
-
AT_END_OF_PERIOD
public static final int AT_END_OF_PERIOD
Flag used to indicate that payment is made at the end of each period.- See Also:
- Constant Field Values
-
-
Method Detail
-
cumipmt
public static double cumipmt(double rate, int nper, double pv, int start, int end, int when)Returns the cumulative interest paid between two periods. It is computed using the following:
where
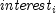 is computed from
is computed from ipmtfor the th period.
th period.- Parameters:
rate- adouble, the interest ratenper- anint, the total number of payment periodspv- adouble, the present valuestart- anint, the first period in the caclulation. Periods are numbered starting with one.end- anint, the last period in the calculationwhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the cumulative interest paid between the first period and the last period - See Also:
- Example
-
cumprinc
public static double cumprinc(double rate, int nper, double pv, int start, int end, int when)Returns the cumulative principal paid between two periods. It is computed using the following:
where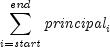
 is computed from
is computed from ppmtfor the th period.
th period.- Parameters:
rate- adouble, the interest ratenper- anint, the total number of payment periodspv- adouble, the present valuestart- anint, the first period in the calculation. Periods are numbered starting with one.end- anint, the last period in the calculationwhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD.- Returns:
- a
double, the cumulative principal paid between the first period and the last period - See Also:
- Example
-
db
public static double db(double cost, double salvage, int life, int period, int month)Returns the depreciation of an asset using the fixed-declining balance method. Methoddbvaries depending on the specified value for the argument period, see table below.If period = 1,
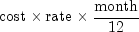
If period = life,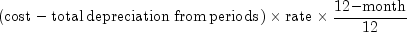
If period other than 1 or life,
where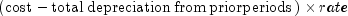
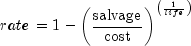
NOTE:
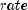 is rounded to three decimal places.
is rounded to three decimal places.- Parameters:
cost- adouble, the initial cost of the assetsalvage- adouble, the salvage value of the assetlife- anint, the number of periods over which the asset is being depreciatedperiod- anint, the period for which the depreciation is to be computedmonth- anint, the number of months in the first year- Returns:
- a
double, the depreciation of an asset for a specified period using the fixed-declining balance method - See Also:
- Example
-
ddb
public static double ddb(double cost, double salvage, int life, int period, double factor)Returns the depreciation of an asset using the double-declining balance method. It is computed using the following:![left[ {{it cost} - {it salvage}left(
{it {total,depreciation,from,prior,periods}} right)} right],
{{{it factor} over {it life}}}](eqn_0372.png)
- Parameters:
cost- adouble, the initial cost of the assetsalvage- adouble, the salvage value of the assetlife- anint, the number of periods over which the asset is being depreciatedperiod- anint, the periodfactor- adouble, the rate at which the balance declines- Returns:
- a
double, the depreciation of an asset for a specified period - See Also:
- Example
-
dollarde
public static double dollarde(double fractionalDollar, int fraction)Converts a fractional price to a decimal price. It is computed using the following: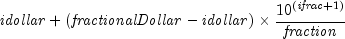
where
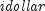 is the integer part of
is the integer part of 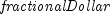 , and
, and
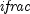 is the integer part of
is the integer part of
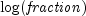 .
.- Parameters:
fractionalDollar- adouble, a fractional numberfraction- anint, the denominator- Returns:
- a
double, the dollar price expressed as a decimal number - See Also:
- Example
-
dollarfr
public static double dollarfr(double decimalDollar, int fraction)Converts a decimal price to a fractional price. It is computed using the following:
where
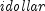 is the integer part of the
is the integer part of the
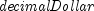 , and
, and 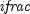 is the integer part of
is the integer part of 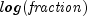 .
.- Parameters:
decimalDollar- adouble, a decimal numberfraction- anint, the denominator- Returns:
- a
double, a dollar price expressed as a fraction - See Also:
- Example
-
effect
public static double effect(double nominalRate, int nper)Returns the effective annual interest rate. The nominal interest rate is the periodically-compounded interest rate as stated on the face of a security. The effective annual interest rate is computed using the following: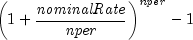
- Parameters:
nominalRate- adouble, the nominal interest ratenper- anint, the number of compounding periods per year- Returns:
- a
double, the effective annual interest rate - See Also:
- Example
-
fv
public static double fv(double rate, int nper, double pmt, double pv, int when)Returns the future value of an investment. The future value is the value, at some time in the future, of a current amount and a stream of payments. It can be found by solving the following:If
 ,
, 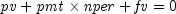
If
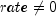 ,
, ![{it pv}
(1 + {it rate})^{it nper} + {it pmt} left[ {1 + {it rate} left(
{it when} right)} right] {{(1 + {it rate})^{it nper} - 1} over
{it rate}} + {it fv} = 0](eqn_0387.png)
- Parameters:
rate- adouble, the interest ratenper- anint, the total number of payment periodspmt- adouble, the payment made in each periodpv- adouble, the present valuewhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the future value of an investment - See Also:
- Example
-
fvschedule
public static double fvschedule(double principal, double[] schedule)Returns the future value of an initial principal taking into consideration a schedule of compound interest rates. It is computed using the following:
where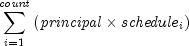
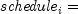 interest rate at the
interest rate at the
 th period, and the count is
th period, and the count is schedule.length.- Parameters:
principal- adouble, the present valueschedule- adoublearray of interest rates to apply- Returns:
- a
double, the future value of an initial principal - See Also:
- Example
-
ipmt
public static double ipmt(double rate, int period, int nper, double pv, double fv, int when)Returns the interest payment for an investment for a given period. It is computed using the following: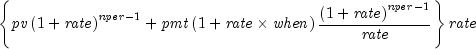
- Parameters:
rate- adouble, the interest rateperiod- anint, the payment periodnper- anint, the total number of periodspv- adouble, the present valuefv- adouble, the future valuewhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the interest payment for a given period for an investment - See Also:
- Example
-
irr
public static double irr(double[] pmt)
Returns the internal rate of return for a schedule of cash flows. It is found by solving the following:
where
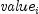 = the
= the 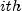 cash flow,
cash flow, 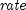 is the internal rate of return, and count is
is the internal rate of return, and count is pmt.length.- Parameters:
pmt- adoublearray which contains cash flow values which occur at regular intervals- Returns:
- a
double, the internal rate of return - See Also:
- Example
-
irr
public static double irr(double[] pmt, double guess)Returns the internal rate of return for a schedule of cash flows. It is found by solving the following:
where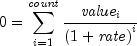
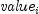 = the
= the 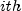 cash flow,
cash flow, 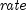 is the internal rate of return.
is the internal rate of return.- Parameters:
pmt- adoublearray which contains cash flow values which occur at regular intervalsguess- adoublevalue which represents an initial guess at the return value from this function- Returns:
- a
double, the internal rate of return
-
mirr
public static double mirr(double[] value, double financeRate, double reinvestRate)Returns the modified internal rate of return for a schedule of periodic cash flows. The modified internal rate of return differs from the ordinary internal rate of return in assuming that the cash flows are reinvested at the cost of capital, not at the internal rate of return. It also eliminates the multiple rates of return problem. It is computed using the following:
where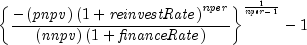
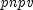 is calculated from
is calculated from npvfor positive values invalueusingreinvestRate,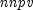 is calculated from
is calculated from npvfor negative values invalueusingfinanceRate, andnper=value.length.- Parameters:
value- adoublearray of cash flowsfinanceRate- adouble, the interest you pay on the money you borrowreinvestRate- adouble, the interest rate you receive on the cash flows- Returns:
- a
double, the modified internal rate of return - See Also:
- Example
-
nominal
public static double nominal(double effectiveRate, int nper)Returns the nominal annual interest rate. The nominal interest rate is the interest rate as stated on the face of a security. It is computed using the following:![left[ {left( {1 + {it effectiveRate}}
right)^{^{{1 over {it nper}}} } - 1} right] times {it nper}](eqn_0403.png)
- Parameters:
effectiveRate- adouble, the effective interest ratenper- anint, the number of compounding periods per year- Returns:
- a
double, the nominal annual interest rate - See Also:
- Example
-
nper
public static double nper(double rate, double pmt, double pv, double fv, int when)Returns the number of periods for an investment for which periodic, and constant payments are made and the interest rate is constant. It can be found by solving the following:If
 ,
, 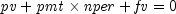
If
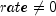 ,
, ![{it pv}
(1 + {it rate})^{it nper} + {it pmt} left[ {1 + {it rate} left(
{it when} right)} right] {{(1 + {it rate})^{it nper} - 1} over
{it rate}} + {it fv} = 0](eqn_0407.png)
- Parameters:
rate- adouble, the interest ratepmt- adouble, the paymentpv- adouble, the present valuefv- adouble, the future valuewhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- an
int, the number of periods for an investment - See Also:
- Example
-
npv
public static double npv(double rate, double[] value)Returns the net present value of a stream of equal periodic cash flows, which are subject to a given discount rate. It is found by solving the following:
where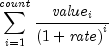
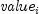 = the
= the  th cash flow, and count is
th cash flow, and count is value.length.- Parameters:
rate- adouble, the interest rate per period. It must not be -1.value- adoublearray of equally-spaced cash flows- Returns:
- a
double, the net present value of the investment - See Also:
- Example
-
pmt
public static double pmt(double rate, int nper, double pv, double fv, int when)Returns the periodic payment for an investment. It can be found by solving the following:If
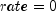 ,
, 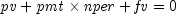
If
 ,
, ![{it pv}(1 + {it rate})^{it nper} + {it pmt} left[ {1 + {it rate}
left( {it when} right)} right] {{(1 + {it rate})^{it nper} - 1}
over {it rate}} + {it fv} = 0](eqn_0414.png)
- Parameters:
rate- adouble, the interest ratenper- anint, the total number of periodspv- adouble, the present valuefv- adouble, the future valuewhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the interest payment for a given period for an investment - See Also:
- Example
-
ppmt
public static double ppmt(double rate, int period, int nper, double pv, double fv, int when)Returns the payment on the principal for a specified period. It is computed using the following:
where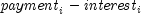
 is computed from
is computed from
pmtfor the th period,
th period,
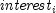 is calculated from
is calculated from ipmtfor the th period.
th period.- Parameters:
rate- adouble, the interest rateperiod- anint, the payment periodnper- anint, the total number of periodspv- adouble, the present valuefv- adouble, the future valuewhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the payment on the principal for a given period - See Also:
- Example
-
pv
public static double pv(double rate, int nper, double pmt, double fv, int when)Returns the net present value of a stream of equal periodic cash flows, which are subject to a given discount rate. It can be found by solving the following:If
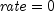 ,
, 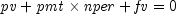
If
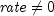 ,
, ![{it pv}(1 + {it rate})^{it nper} + {it pmt} left[ {1 + {it rate}
left( {it when} right)} right] {{(1 + {it rate})^{it nper} - 1}
over {it rate}} + {it fv} = 0](eqn_0423.png)
- Parameters:
rate- adouble, the interest rate per periodnper- anint, the number of periodspmt- adouble, the payment made each periodfv- adouble, the annuity's value after the last paymentwhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the present value of the investment - See Also:
- Example
-
rate
public static double rate(int nper, double pmt, double pv, double fv, int when)Returns the interest rate per period of an annuity. rate is calculated by iteration and can have zero or more solutions. It can be found by solving the following:If
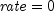 ,
, 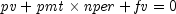
If
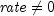 ,
, ![{it pv}(1 + {it rate})^{it nper} + {it pmt} left[ {1 + {it rate}
left( {it when} right)} right] {{(1 + {it rate})^{it nper} - 1}
over {it rate}} + {it fv} = 0](eqn_0427.png)
- Parameters:
nper- anint, the number of periodspmt- adouble, the payment made each periodpv- adouble, the present valuefv- adouble, the annuity's value after the last paymentwhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIOD- Returns:
- a
double, the interest rate per period of an annuity - See Also:
- Example
-
rate
public static double rate(int nper, double pmt, double pv, double fv, int when, double guess)Returns the interest rate per period of an annuity with an initial guess. rate is calculated by iteration and can have zero or more solutions. It can be found by solving the following:If
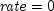 ,
, 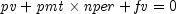
If
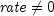 ,
, ![{it pv}(1 + {it rate})^{it nper} + {it pmt} left[ {1 + {it rate}
left( {it when} right)} right] {{(1 + {it rate})^{it nper} - 1}
over {it rate}} + {it fv} = 0](eqn_0431.png)
- Parameters:
nper- anint, the number of periodspmt- adouble, the payment made each periodpv- adouble, the present valuefv- adouble, the annuity's value after the last paymentwhen- anint, the time in each period when the payment is made, eitherAT_END_OF_PERIODorAT_BEGINNING_OF_PERIODguess- adoublevalue which represents an initial guess at the interest rate per period of an annuity- Returns:
- a
double, the interest rate per period of an annuity - See Also:
- Example
-
sln
public static double sln(double cost, double salvage, int life)Returns the depreciation of an asset using the straight line method. It is computed using the following: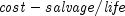
- Parameters:
cost- adouble, the initial cost of the assetsalvage- adouble, the salvage value of the assetlife- anint, the number of periods over which the asset is being depreciated- Returns:
- a
double, the straight line depreciation of an asset for one period - See Also:
- Example
-
syd
public static double syd(double cost, double salvage, int life, int per)Returns the depreciation of an asset using the sum-of-years digits method. It is computed using the following: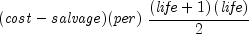
- Parameters:
cost- adouble, the initial cost of the assetsalvage- adouble, the salvage value of the assetlife- anint, the number of periods over which the asset is being depreciatedper- anint, the period- Returns:
- a
double, the sum-of-years digits depreciation of an asset - See Also:
- Example
-
vdb
public static double vdb(double cost, double salvage, int life, int start, int end, double factor, boolean no_sl)Returns the depreciation of an asset for any given period using the variable-declining balance method. It is computed using the following:If
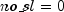 ,
, 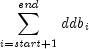
If
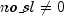 ,
,
where
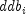 is computed from
is computed from ddbfor the th
period.
th
period. 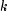 = the first period where straight line
depreciation is greater than the depreciation using the double-declining
balance method.
= the first period where straight line
depreciation is greater than the depreciation using the double-declining
balance method.

- Parameters:
cost- adouble, the initial cost of the assetsalvage- adouble, the salvage value of the assetlife- anint, the number of periods over which the asset is being depreciatedstart- anint, the initial period for the calculationend- anint, the final period for the calculationfactor- adouble, the rate at which the balance declinesno_sl- abooleanflag. If true, do not switch to straight-line depreciation even when the depreciation is greater than the declining balance calculation.- Returns:
- a
double, the depreciation of the asset - See Also:
- Example
-
xirr
public static double xirr(double[] pmt, Date[] dates)Returns the internal rate of return for a schedule of cash flows. It is not necessary that the cash flows be periodic. It can be found by solving the following:
In the equation above,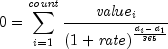
 represents the
represents the
 th payment date.
th payment date. 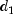 represents the 1st payment date.
represents the 1st payment date. 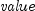 represents the
represents the  th cash flow.
th cash flow.
 is the internal rate of return, and count is
is the internal rate of return, and count is pmt.length.- Parameters:
pmt- adoublearray which contains cash flow values which correspond to a schedule of payments in datesdates- aDatearray which contains a schedule of payment dates- Returns:
- a
double, the internal rate of return - See Also:
- Example
-
xirr
public static double xirr(double[] pmt, Date[] dates, double guess)Returns the internal rate of return for a schedule of cash flows with a user supplied initial guess. It is not necessary that the cash flows be periodic. It can be found by solving the following:
In the equation above,
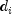 represents the
represents the
 th payment date.
th payment date.  represents the 1st payment date.
represents the 1st payment date. 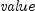 represents the
represents the  th cash flow.
th cash flow.
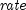 is the internal rate of return. Count is
is the internal rate of return. Count is pmt.length.- Parameters:
pmt- adoublearray which contains cash flow values which correspond to a schedule of payments in datesdates- aDatearray which contains a schedule of payment datesguess- adoublevalue which represents an initial guess at the return value from this function- Returns:
- a
double, the internal rate of return
-
xnpv
public static double xnpv(double rate, double[] value, Date[] dates)Returns the present value for a schedule of cash flows. It is not necessary that the cash flows be periodic. It is computed using the following:
In the equation above,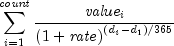
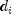 represents the
represents the
 th payment date,
th payment date, 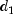 represents
the first payment date,
represents
the first payment date, 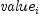 represents
the
represents
the  th cash flow. and count is
th cash flow. and count is value.length- Parameters:
rate- adouble, the interest ratevalue- adoublearray containing the cash flowsdates- aDatearray which contains a schedule of payment dates- Returns:
- a
double, the present value - See Also:
- Example
-
-