- java.lang.Object
-
- com.imsl.math.Cholesky
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class Cholesky extends Object implements Serializable, Cloneable
Cholesky factorization of a matrix of typedouble.Class
Choleskyuses the Cholesky-Banachiewicz algortithm to factor the matrix A.The Cholesky factorization of a matrix is
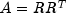 ,
where R is a lower triangular matrix. Thus,
,
where R is a lower triangular matrix. Thus,
which leads to the following for the entries of the lower triangular marix R: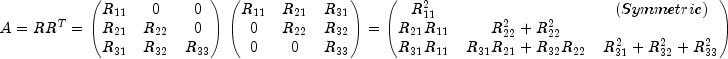
and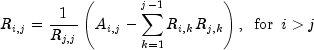
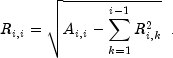
The method
updateis based on the LINPACK routineSCHUD; see Dongarra et al. (1979) and updates the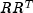 Cholesky factorization
of the real symmetric positive definite matrix A after a rank-one matrix is added.
Given this factorization,
Cholesky factorization
of the real symmetric positive definite matrix A after a rank-one matrix is added.
Given this factorization, updatecomputes the factorization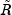 such that
such that
Similarly, the method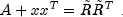
downdate, based on the LINPACK routineSCHDD; see Dongarra et al. (1979), downdates the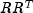 Cholesky factorization
of the real symmetric positive definite matrix A after a rank-one matrix is subtracted.
Cholesky factorization
of the real symmetric positive definite matrix A after a rank-one matrix is subtracted.
downdatecomputes the factorization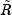 such that
such that
This is not always possible, since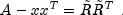
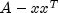 may not be positive definite.
may not be positive definite.
downdatedetermines an orthogonal matrix U as the product of Givens rotations, such that
of Givens rotations, such that
![U
left[ begin{array}{l} R^T \ 0 \ end{array} right] =
left[ begin{array}{l} {tilde R}^T \ x^T \ end{array} right]](eqn_1899.png)
By multiplying this equation by its transpose and noting that
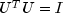 ,
the desired result
,
the desired result
is obtained.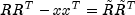
Let a be the solution of the linear system
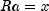 and let
and let
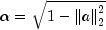
The Givens rotations,
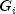 , are chosen such that
, are chosen such that
![G_1 cdots G_N
left[ begin{array}{l}a \ alpha end{array} right] =
left[ begin{array}{l} 0 \ 1 end{array} right]](eqn_1905.png)
The
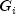 , are (N + 1) by (N + 1) matrices of the form
, are (N + 1) by (N + 1) matrices of the form
where![G_i =
left[ {begin{array}{*{20}c}{
I_{i - 1} } & 0 & 0 & 0 \
0 & {c_i } & 0 & { - s_i } \
0 & 0 & {I_{N - i} } & 0 \
0 & {s_i } & 0 & {c_i } \
end{array}} right]](eqn_1907.png)
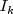 is the identity matrix of order k;
and
is the identity matrix of order k;
and 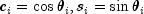 for some
for some
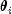 .
.
The Givens rotations are then used to form
![{tilde R}^T,,,G_1 cdots ,G_N
left[ begin{array}{l} R^T \ 0 \ end{array} right] =
left[ begin{array}{l} {tilde R}^T \ {tilde x^T} \ end{array} right]](eqn_1911.png)
The matrix
is lower triangular and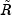
because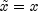
.![x = left( {R ,,, 0} right)
left[ begin{array}{l}a \ alpha \ end{array} right] =
left( R ,,, 0 right)
U^TU left[ begin{array}{l}a \ alpha \ end{array} right] =
left( {tilde R ,,, tilde x} right)
left[ begin{array}{l}0 \ 1 \ end{array} right] =
tilde x](eqn_1914.png)
- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classCholesky.NotSPDExceptionThe matrix is not symmetric, positive definite.
-
Constructor Summary
Constructors Constructor and Description Cholesky(double[][] a)Create the Cholesky factorization of a symmetric positive definite matrix of typedouble.
-
Method Summary
Methods Modifier and Type Method and Description voiddowndate(double[] x)Downdates the factorization by subtracting a rank-1 matrix.double[][]getR()Returns the R matrix that results from the Cholesky factorization.double[][]inverse()Returns the inverse of this matrixdouble[]solve(double[] b)Solve Ax = b where A is a positive definite matrix with elements of typedouble.voidupdate(double[] x)Updates the factorization by adding a rank-1 matrix.
-
-
-
Constructor Detail
-
Cholesky
public Cholesky(double[][] a) throws SingularMatrixException, Cholesky.NotSPDExceptionCreate the Cholesky factorization of a symmetric positive definite matrix of typedouble.- Parameters:
a- adoublesquare matrix to be factored- Throws:
IllegalArgumentException- Thrown when the row lengths of matrix a are not equal (for example, the matrix edges are "jagged".)SingularMatrixException- Thrown when the input matrix A is singular.Cholesky.NotSPDException- Thrown when the input matrix is not symmetric, positive definite.
-
-
Method Detail
-
downdate
public void downdate(double[] x) throws Cholesky.NotSPDExceptionDowndates the factorization by subtracting a rank-1 matrix. The object will contain the Cholesky factorization of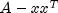 , where A is the previously factored matrix.
, where A is the previously factored matrix.- Parameters:
x- Adoublearray which specifies the rank-1 matrix.xis not modified by this function.- Throws:
Cholesky.NotSPDException- if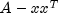 is not symmetric
positive-definite.
is not symmetric
positive-definite.
-
getR
public double[][] getR()
Returns the R matrix that results from the Cholesky factorization.- Returns:
- a
doublematrix which contains the lower triangular R matrix that results from the Cholesky factorization such that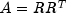
-
inverse
public double[][] inverse()
Returns the inverse of this matrix- Returns:
- a
doublematrix containing the inverse
-
solve
public double[] solve(double[] b)
Solve Ax = b where A is a positive definite matrix with elements of typedouble.- Parameters:
b- adoublearray containing the right-hand side of the linear system- Returns:
- a
doublearray containing the solution to the system of linear equations
-
update
public void update(double[] x)
Updates the factorization by adding a rank-1 matrix. The object will contain the Cholesky factorization of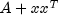 , where A is the previously factored
matrix.
, where A is the previously factored
matrix.- Parameters:
x- Adoublearray which specifies the rank-1 matrix.xis not modified by this function.
-
-