- java.lang.Object
-
- com.imsl.math.ComplexSparseCholesky
-
- All Implemented Interfaces:
- Serializable
public class ComplexSparseCholesky extends Object implements Serializable
Sparse Cholesky factorization of a matrix of typeComplexSparseMatrix.Class
ComplexSparseCholeskycomputes the Cholesky factorization of a sparse Hermitian positive definite matrix A. This factorization can then be used to compute the solution of the linear system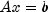 .
.Typically, the solution of a large sparse positive definite system
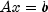 is done in four steps.
is done in four steps.- In the first step, an ordering algorithm is used to preserve sparsity in the Cholesky factor L of matrix A during the numerical factorization process. The new order can be described by a permutation matrix P.
- Step two consists of setting up the data structure for the Cholesky factor
L, where
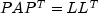 . This step is called the
symbolic factorization phase of the computation. During symbolic
factorization, only the sparsity pattern of sparse matrix A, i.e.,
the locations of the nonzero entries of matrix A are needed but not
any of the elements themselves.
. This step is called the
symbolic factorization phase of the computation. During symbolic
factorization, only the sparsity pattern of sparse matrix A, i.e.,
the locations of the nonzero entries of matrix A are needed but not
any of the elements themselves.
- In step 3, the numerical factorization phase, the Cholesky factorization is done numerically.
- Step 4 is the solution phase. Here, the numerical
solution, x, to the original system is obtained by solving the two
triangular systems
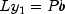 ,
, 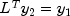 and the permutation
and the permutation  .
.
Class
ComplexSparseCholeskyrealizes all four steps by algorithms described in George and Liu (1981). Especially, step one, is a realization of a minimum degree ordering algorithm. The numerical factorization in its standard form is based on a sparse compressed storage scheme. Alternatively, a multifrontal method can be used. The multifrontal method requires more storage but will be faster than the standard method in certain cases. The multifrontal method is based on the routines in Liu (1987). For a detailed description of this method, see Liu (1990), also Duff and Reid(1983, 1984), Ashcraft (1987) et al. (1987), and Liu (1986, 1989, 1992). The numerical factorization method can be specified by using thesetNumericFactorizationMethodThe
solvefactorSymbolicallyfactorNumericallysetNumericFactorsetSymbolicFactorsolvemethod when different right-hand sides are to be solved.There is a special situation where computations can be simplified. If an application generates different sparse Hermitian positive definite coefficient matrices that all have the same sparsity pattern, then by using methods
getSymbolicFactorsetSymbolicFactor- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classComplexSparseCholesky.NotSPDExceptionThe matrix is not Hermitian, positive definite.static classComplexSparseCholesky.NumericFactorData structures and functions for the numeric Cholesky factor.static classComplexSparseCholesky.SymbolicFactorData structures and functions for the symbolic Cholesky factor.
-
Field Summary
Fields Modifier and Type Field and Description static intMULTIFRONTAL_METHODIndicates the multifrontal method will be used for numeric factorization.static intSTANDARD_METHODIndicates that the method of George/Liu (1981) is used for numeric factorization.
-
Constructor Summary
Constructors Constructor and Description ComplexSparseCholesky(ComplexSparseMatrix A)Constructs the matrix structure for the Cholesky factorization of a sparse Hermitian positive definite matrix of typeComplexSparseMatrix.
-
Method Summary
Methods Modifier and Type Method and Description voidfactorNumerically()Computes the numeric factorization of a sparse Hermitian positive definite matrix.voidfactorSymbolically()Computes the symbolic factorization of a sparse Hermitian positive definite matrix.doublegetLargestDiagonalElement()Returns the largest diagonal element of the Cholesky factor.longgetNumberOfNonzeros()Returns the number of nonzeros in the Cholesky factor.ComplexSparseCholesky.NumericFactorgetNumericFactor()Returns the numeric Cholesky factor.intgetNumericFactorizationMethod()Returns the method used in the numerical factorization of the permuted input matrix.doublegetSmallestDiagonalElement()Returns the smallest diagonal element of the Cholesky factor.ComplexSparseCholesky.SymbolicFactorgetSymbolicFactor()Returns the symbolic Cholesky factor.voidsetNumericFactor(ComplexSparseCholesky.NumericFactor numericFactor)Sets the numeric Cholesky factor to use in solving a sparse complex Hermitian positive definite system of linear equations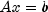 .
.voidsetNumericFactorizationMethod(int method)Defines the method used in the numerical factorization of the permuted input matrix.voidsetSymbolicFactor(ComplexSparseCholesky.SymbolicFactor symbolicFactor)Sets the symbolic Cholesky factor to use in solving a sparse complex Hermitian positive definite system of linear equations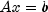 .
.Complex[]solve(Complex[] b)Computes the solution of a sparse Hermitian positive definite system of linear equations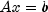 .
.
-
-
-
Field Detail
-
MULTIFRONTAL_METHOD
public static final int MULTIFRONTAL_METHOD
Indicates the multifrontal method will be used for numeric factorization.- See Also:
- Constant Field Values
-
STANDARD_METHOD
public static final int STANDARD_METHOD
Indicates that the method of George/Liu (1981) is used for numeric factorization.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
ComplexSparseCholesky
public ComplexSparseCholesky(ComplexSparseMatrix A)
Constructs the matrix structure for the Cholesky factorization of a sparse Hermitian positive definite matrix of typeComplexSparseMatrix.- Parameters:
A- TheComplexSparseMatrixHermitian positive definite matrix to be factored. Only the lower triangular part of the input matrix is used.
-
-
Method Detail
-
factorNumerically
public void factorNumerically() throws ComplexSparseCholesky.NotSPDExceptionComputes the numeric factorization of a sparse Hermitian positive definite matrix.This method numerically factors the instance of the constructed matrix A, where A is of type
ComplexSparseMatrixand is Hermitian positive definite. The factorization is obtained in several steps:- First, matrix A is permuted to reduce fill-in, leading to
a sparse Hermitian positive definite matrix
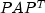 .
. - Then, matrix
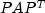 is symbolically and
numerically factored.
is symbolically and
numerically factored.
Note that the symbolic factorization is not done if the symbolic factor has been supplied by the user through the
setSymbolicFactormethod.- Throws:
ComplexSparseCholesky.NotSPDException- is thrown if the input matrix is not Hermitian, positive definite.
- First, matrix A is permuted to reduce fill-in, leading to
a sparse Hermitian positive definite matrix
-
factorSymbolically
public void factorSymbolically() throws ComplexSparseCholesky.NotSPDExceptionComputes the symbolic factorization of a sparse Hermitian positive definite matrix.This method symbolically factors the instance of the constructed matrix A, where A is of type
ComplexSparseMatrixand is Hermitian positive definite. The factorization is obtained in several steps:- First, matrix A is permuted to reduce fill-in, leading to
a sparse Hermitian positive definite matrix
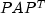 .
. - Then, matrix
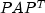 is
symbolically factored.
is
symbolically factored.
- Throws:
ComplexSparseCholesky.NotSPDException- is thrown if the input matrix is not Hermitian, positive definite.
- First, matrix A is permuted to reduce fill-in, leading to
a sparse Hermitian positive definite matrix
-
getLargestDiagonalElement
public double getLargestDiagonalElement()
Returns the largest diagonal element of the Cholesky factor.- Returns:
- a
doublevalue specifying the largest diagonal element of the Cholesky factor. Use of this method is only sensible if a numeric factorization of the input matrix was done beforehand.
-
getNumberOfNonzeros
public long getNumberOfNonzeros()
Returns the number of nonzeros in the Cholesky factor.- Returns:
- a
longvalue specifying the number of nonzeros (including the diagonal) of the Cholesky factor.
-
getNumericFactor
public ComplexSparseCholesky.NumericFactor getNumericFactor()
Returns the numeric Cholesky factor.- Returns:
- a
NumericFactorcontaining the numeric Cholesky factor.
-
getNumericFactorizationMethod
public int getNumericFactorizationMethod()
Returns the method used in the numerical factorization of the permuted input matrix.- Returns:
- an
intvalue equal toSTANDARD_METHOD= 0 orMULTIFRONTAL_METHOD= 1 representing the method used in the numeric factorization of the permuted input matrix. SeesetNumericFactorizationMethodfor more details.
-
getSmallestDiagonalElement
public double getSmallestDiagonalElement()
Returns the smallest diagonal element of the Cholesky factor.- Returns:
- a
doublevalue specifying the smallest diagonal element of the Cholesky factor. Use of this method is only sensible if a numeric factorization of the input matrix was done beforehand.
-
getSymbolicFactor
public ComplexSparseCholesky.SymbolicFactor getSymbolicFactor()
Returns the symbolic Cholesky factor.- Returns:
- a
SymbolicFactorcontaining the symbolic Cholesky factor.
-
setNumericFactor
public void setNumericFactor(ComplexSparseCholesky.NumericFactor numericFactor)
Sets the numeric Cholesky factor to use in solving a sparse complex Hermitian positive definite system of linear equations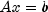 .
.- Parameters:
numericFactor- aNumericFactorobject containing the numeric Cholesky factor. By default the numeric factorization is computed.
-
setNumericFactorizationMethod
public void setNumericFactorizationMethod(int method)
Defines the method used in the numerical factorization of the permuted input matrix.- Parameters:
method- anintvalue specifying the method to choose:Method NameDescription STANDARD_METHODstandard method as described by George/Liu (1981). This is the default. MULTIFRONTAL_METHODmultifrontal method - Throws:
IllegalArgumentException- This exception is thrown when the value for method is notSTANDARD_METHODorMULTIFRONTAL_METHOD.
-
setSymbolicFactor
public void setSymbolicFactor(ComplexSparseCholesky.SymbolicFactor symbolicFactor)
Sets the symbolic Cholesky factor to use in solving a sparse complex Hermitian positive definite system of linear equations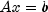 .
.- Parameters:
symbolicFactor- aSymbolicFactorcontaining the symbolic Cholesky factor. By default the symbolic factorization is computed.
-
solve
public Complex[] solve(Complex[] b) throws ComplexSparseCholesky.NotSPDException
Computes the solution of a sparse Hermitian positive definite system of linear equations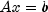 .
.
This method solves the linear system
 , where
A is Hermitian positive definite. The solution is obtained in
several steps:
, where
A is Hermitian positive definite. The solution is obtained in
several steps:
- First, matrix
A is permuted to reduce fill-in, leading to a sparse Hermitian
positive definite system
 .
. - Then, matrix
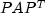 is
symbolically and numerically factored.
is
symbolically and numerically factored. - The final solution is obtained by solving
the systems
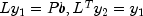 and
and
 .
.
By default this method implements all of the above steps. The factorizations are retained for later use by subsequent solves. By choosing appropriate methods within this class, the computation can be reduced to the solution of the system
 for a given or precomputed symbolic or numeric factor.
for a given or precomputed symbolic or numeric factor. - Parameters:
b- AComplexvector of length equal to the order of A containing the right-hand side.- Returns:
- a
Complexvector of length equal to the order of matrix A containing the solution of the system .
. - Throws:
ComplexSparseCholesky.NotSPDException- is thrown if the input matrix is not Hermitian, positive definite.
- First, matrix
A is permuted to reduce fill-in, leading to a sparse Hermitian
positive definite system
-
-