- java.lang.Object
-
- com.imsl.math.ConjugateGradient
-
- All Implemented Interfaces:
- Serializable
public class ConjugateGradient extends Object implements Serializable
Solves a real symmetric definite linear system using the conjugate gradient method with optional preconditioning.Class
ConjugateGradientsolves the symmetric positive or negative definite linear system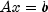 using the conjugate
gradient method with optional preconditioning. This method is described
in detail by Golub and Van Loan (1983, Chapter 10), and in Hageman and
Young (1981, Chapter 7).
using the conjugate
gradient method with optional preconditioning. This method is described
in detail by Golub and Van Loan (1983, Chapter 10), and in Hageman and
Young (1981, Chapter 7).The preconditioning matrix M is a matrix that approximates A, and for which the linear system Mz=r is easy to solve. These two properties are in conflict; balancing them is a topic of current research. If no preconditioning matrix is specified,
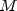 is set to the
identity, i.e.
is set to the
identity, i.e. 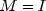 .
.
The number of iterations needed depends on the matrix and the error tolerance. As a rough guide,
where n is the order of matrix A.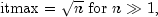
See the references for details.
Let M be the preconditioning matrix, let b,p,r,x and z be vectors and let
 be the desired relative error. Then the
algorithm used is as follows:
be the desired relative error. Then the
algorithm used is as follows: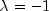
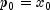
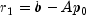
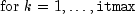
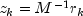
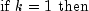
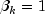
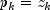
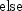
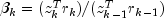
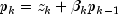
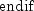
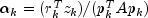
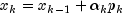
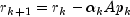
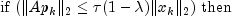
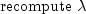
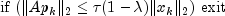
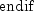
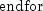
Here,
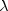 is an estimate of
is an estimate of 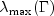 ,
the largest eigenvalue of the iteration matrix
,
the largest eigenvalue of the iteration matrix 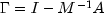 . The stopping criterion
is based on the result (Hageman and Young 1981, pp. 148-151)
. The stopping criterion
is based on the result (Hageman and Young 1981, pp. 148-151)
where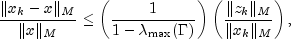
It is also known that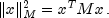
where the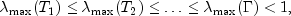
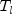 are the symmetric, tridiagonal matrices
are the symmetric, tridiagonal matrices
with![T_l = left[ begin{array}{ccccc}
mu_1 & omega_2 & & & \
omega_2 & mu_2 & omega_3 & & \
& omega_3 & mu_3 & raisebox{-1ex}{ ddots } & \
& & ddots & ddots & omega_l \
& & & omega_l & mu_l
end{array} right]](eqn_1532.png)
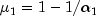 and, for
and, for 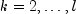 ,
,
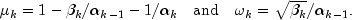
Usually, the eigenvalue computation is needed for only a few of the iterations.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceConjugateGradient.FunctionPublic interface for the user supplied function toConjugateGradient.static classConjugateGradient.NoConvergenceExceptionThe conjugate gradient method did not converge within the allowed maximum number of iterations.static classConjugateGradient.NotDefiniteAMatrixExceptionThe input matrix A is indefinite, that is the matrix is not positive or negative definite.static classConjugateGradient.NotDefiniteJacobiPreconditionerExceptionThe Jacobi preconditioner is not strictly positive or negative definite.static classConjugateGradient.NotDefinitePreconditionMatrixExceptionThe Precondition matrix is indefinite.static interfaceConjugateGradient.PreconditionerPublic interface for the user supplied function toConjugateGradientused for preconditioning.static classConjugateGradient.SingularPreconditionMatrixExceptionThe Precondition matrix is singular.
-
Constructor Summary
Constructors Constructor and Description ConjugateGradient(int n, ConjugateGradient.Function argF)Conjugate gradient constructor.
-
Method Summary
Methods Modifier and Type Method and Description intgetIterations()Returns the number of iterations needed by the conjugate gradient algorithm.double[]getJacobi()Returns the Jacobi preconditioning matrix.intgetMaxIterations()Returns the maximum number of iterations allowed.doublegetRelativeError(double errorRelative)Returns the relative error used for stopping the algorithm.voidsetJacobi(double[] diagonal)Defines a Jacobi preconditioner as the preconditioning matrix, that is, M is the diagonal ofA.voidsetMaxIterations(int maxIterations)Sets the maximum number of iterations allowed.voidsetRelativeError(double tolerance)Sets the relative error used for stopping the algorithm.double[]solve(double[] b)Solves a real symmetric positive or negative definite system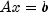 using
a conjugate gradient method with or without preconditioning.
using
a conjugate gradient method with or without preconditioning.
-
-
-
Constructor Detail
-
ConjugateGradient
public ConjugateGradient(int n, ConjugateGradient.Function argF)Conjugate gradient constructor.- Parameters:
n- anintscalar value defining the order of the matrix.argF- aFunctionthat defines the user-supplied function which computes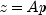 .
If
.
If argFimplementsPreconditionerthen right preconditioning is performed using this user supplied function. Otherwise, no preconditioning is performed. Note thatargFcan be used to act upon the coefficients of matrix A stored in different storage modes.
-
-
Method Detail
-
getIterations
public int getIterations()
Returns the number of iterations needed by the conjugate gradient algorithm.- Returns:
- an
intvalue indicating the number of iterations needed.
-
getJacobi
public double[] getJacobi()
Returns the Jacobi preconditioning matrix.- Returns:
- a
doublevectordiagonalcontaining the diagonal of the Jacobi preconditioner M, that is,diagonal[i]=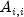 ,
A the input matrix.
,
A the input matrix.
-
getMaxIterations
public int getMaxIterations()
Returns the maximum number of iterations allowed.- Returns:
- an
intvalue specifying the maximum number of iterations allowed.
-
getRelativeError
public double getRelativeError(double errorRelative)
Returns the relative error used for stopping the algorithm.- Returns:
- a
doublecontaining the relative error.
-
setJacobi
public void setJacobi(double[] diagonal)
Defines a Jacobi preconditioner as the preconditioning matrix, that is, M is the diagonal ofA.- Parameters:
diagonal- adoublevector containing the diagonal of A as the Jacobi preconditioner M, that is,diagonal[i]=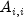 .
.- Throws:
IllegalArgumentException- is thrown if the length of vectordiagonalis not equal to the ordernof input matrix A.
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Sets the maximum number of iterations allowed.- Parameters:
maxIterations- anintvalue specifying the maximum number of iterations allowed. By default,maxIterations=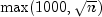 .
.- Throws:
IllegalArgumentException- is thrown ifmaxIterationsis less than or equal to 0.
-
setRelativeError
public void setRelativeError(double tolerance)
Sets the relative error used for stopping the algorithm.- Parameters:
tolerance- adoublespecifying the relative error. By default,tolerance= 1.49e-08, the square root of the precision.- Throws:
IllegalArgumentException- is thrown iftoleranceis less than 0.
-
solve
public double[] solve(double[] b) throws ConjugateGradient.SingularPreconditionMatrixException, ConjugateGradient.NotDefinitePreconditionMatrixException, SingularMatrixException, ConjugateGradient.NotDefiniteAMatrixException, ConjugateGradient.NoConvergenceException, ConjugateGradient.NotDefiniteJacobiPreconditionerExceptionSolves a real symmetric positive or negative definite system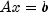 using
a conjugate gradient method with or without preconditioning.
using
a conjugate gradient method with or without preconditioning.- Parameters:
b- adoublevector of lengthncontaining the right-hand side.- Returns:
- a
doublevector of lengthncontaining the approximate solution to the linear system. - Throws:
IllegalArgumentException- is thrown if the length ofbis not consistent with the ordernofA.ConjugateGradient.SingularPreconditionMatrixException- is thrown if the preconditioning matrix is singular.ConjugateGradient.NotDefinitePreconditionMatrixException- is thrown if the preconditioning matrix is not definite.SingularMatrixException- is thrown if input matrix A is singular.ConjugateGradient.NotDefiniteAMatrixException- is thrown if matrix A is not definite.ConjugateGradient.NoConvergenceException- is thrown if the algorithm is not convergent withinmaxIterationsiterations.ConjugateGradient.NotDefiniteJacobiPreconditionerException- is thrown if the Jacobi preconditioner is not definite.
-
-