- java.lang.Object
-
- com.imsl.math.Spline
-
- com.imsl.math.CsInterpolate
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class CsInterpolate extends Spline
Extension of the Spline class to interpolate data points.CsInterpolatecomputes a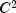 cubic spline
interpolant to a set of data points
cubic spline
interpolant to a set of data points 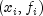 for
for
 . The breakpoints of the spline are the
abscissas. Endpoint conditions can be automatically determined by the program,
or explicitly specified by using the appropriate constructor. Constructors are
provided that allow setting specific values for first or second derivative values
at the endpoints, or for specifying conditions that correspond to the "not-a-knot"
condition (see de Boor 1978).
. The breakpoints of the spline are the
abscissas. Endpoint conditions can be automatically determined by the program,
or explicitly specified by using the appropriate constructor. Constructors are
provided that allow setting specific values for first or second derivative values
at the endpoints, or for specifying conditions that correspond to the "not-a-knot"
condition (see de Boor 1978).
The "not-a-knot" conditions require that the third derivative of the spline be continuous at the second and next-to-last breakpoint. If n is 2 or 3, then the linear or quadratic interpolating polynomial is computed, respectively.
If the data points arise from the values of a smooth, say,
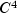 function f, i.e.
function f, i.e.
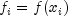 , then the error will behave in a
predictable fashion. Let
, then the error will behave in a
predictable fashion. Let 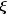 be the breakpoint
vector for the above spline interpolant. Then, the maximum absolute error
satisfies
be the breakpoint
vector for the above spline interpolant. Then, the maximum absolute error
satisfies![|f-s|_{[xi_0,xi_n]} le C left|f^{(4)}right|_{[{xi_0 ,xi_n }]} |xi|^4](eqn_1490.png)
where
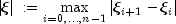
For more details, see de Boor (1978, pages 55-56).
- See Also:
- Example, Serialized Form
-
-
Field Summary
Fields Modifier and Type Field and Description static intFIRST_DERIVATIVEstatic intNOT_A_KNOTstatic intSECOND_DERIVATIVE-
Fields inherited from class com.imsl.math.Spline
breakPoint, coef, EPSILON_LARGE
-
-
Constructor Summary
Constructors Constructor and Description CsInterpolate(double[] xData, double[] yData)Constructs a cubic spline that interpolates the given data points.CsInterpolate(double[] xData, double[] yData, int typeLeft, double valueLeft, int typeRight, double valueRight)Constructs a cubic spline that interpolates the given data points with specified derivative endpoint conditions.
-
Method Summary
-
Methods inherited from class com.imsl.math.Spline
copyAndSortData, copyAndSortData, derivative, derivative, derivative, getBreakpoints, integral, value, value
-
-
-
-
Field Detail
-
FIRST_DERIVATIVE
public static final int FIRST_DERIVATIVE
- See Also:
- Constant Field Values
-
NOT_A_KNOT
public static final int NOT_A_KNOT
- See Also:
- Constant Field Values
-
SECOND_DERIVATIVE
public static final int SECOND_DERIVATIVE
- See Also:
- Constant Field Values
-
-
Constructor Detail
-
CsInterpolate
public CsInterpolate(double[] xData, double[] yData)Constructs a cubic spline that interpolates the given data points. The interpolant satisfies the "not-a-knot" condition.- Parameters:
xData- Adoublearray containing the x-coordinates of the data. Values must be distinct.yData- Adoublearray containing the y-coordinates of the data. The arrays xData and yData must have the same length.
-
CsInterpolate
public CsInterpolate(double[] xData, double[] yData, int typeLeft, double valueLeft, int typeRight, double valueRight)Constructs a cubic spline that interpolates the given data points with specified derivative endpoint conditions.- Parameters:
xData- Adoublearray containing the x-coordinates of the data. Values must be distinct.yData- Adoublearray containing the y-coordinates of the data. The arrays xData and yData must have the same length.typeLeft- Anintdenoting the type of condition at the left endpoint. This can beNOT_A_KNOT,FIRST_DERIVATIVEorSECOND_DERIVATIVE.valueLeft- Adoublevalue at the left endpoint. IftypeLeftisNOT_A_KNOTthis is ignored, Otherwise, it is the value of the specified derivative.typeRight- Anintdenoting the type of condition at the right endpoint. This can beNOT_A_KNOT,FIRST_DERIVATIVEorSECOND_DERIVATIVE.valueRight- Adoublevalue at the right endpoint.
-
-