- java.lang.Object
-
- com.imsl.math.Eigen
-
public class Eigen extends Object
Collection of Eigen System functions.Eigencomputes the eigenvalues and eigenvectors of a real matrix. The matrix is first balanced. Orthogonal similarity transformations are used to reduce the balanced matrix to a real upper Hessenberg matrix. The implicit double-shifted QR algorithm is used to compute the eigenvalues and eigenvectors of this Hessenberg matrix. The eigenvectors are normalized such that each has Euclidean length of value one. The largest component is real and positive.The balancing routine is based on the EISPACK routine
BALANC. The reduction routine is based on the EISPACK routinesORTHESandORTRAN. The QR algorithm routine is based on the EISPACK routineHQR2. See Smith et al. (1976) for the EISPACK routines. Further details, some timing data, and credits are given in Hanson et al. (1990).While the exact value of the performance index,
 ,
is highly machine dependent, the performance of
,
is highly machine dependent, the performance of Eigenis considered excellent if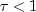 , good if
, good if
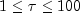 , and poor if
, and poor if
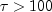 .
.The performance index was first developed by the EISPACK project at Argonne National Laboratory; see Smith et al. (1976, pages 124-125).
- See Also:
- Example
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classEigen.DidNotConvergeExceptionThe iteration did not converge
-
Constructor Summary
Constructors Constructor and Description Eigen()Constructs the eigenvalues and the eigenvectors of a real square matrix.
-
Method Summary
Methods Modifier and Type Method and Description intgetMaxIterations()Returns the maximum number of iterations.Complex[]getValues()Returns the eigenvalues of a matrix of typedouble.Complex[][]getVectors()Returns the eigenvectors.doubleperformanceIndex(double[][] a)Returns the performance index of a real eigensystem.voidsetMaxIterations(int maxIterations)Set the maximum number of iterations allowed.voidsolve(double[][] a, boolean computeVectors)Solves for the eigenvalues and (optionally) the eigenvectors of a real square matrix.
-
-
-
Constructor Detail
-
Eigen
public Eigen()
Constructs the eigenvalues and the eigenvectors of a real square matrix.
-
-
Method Detail
-
getMaxIterations
public int getMaxIterations()
Returns the maximum number of iterations.- Returns:
- an
intcontaining the maximum number of iterations.
-
getValues
public Complex[] getValues()
Returns the eigenvalues of a matrix of typedouble.- Returns:
- a
Complexarray containing the eigenvalues of this matrix in descending order
-
getVectors
public Complex[][] getVectors()
Returns the eigenvectors.- Returns:
- A
Complexmatrix containing the eigenvectors. The eigenvector corresponding to the j-th eigenvalue is stored in the j-th column. Each vector is normalized to have Euclidean length one.
-
performanceIndex
public double performanceIndex(double[][] a)
Returns the performance index of a real eigensystem.- Parameters:
a- adoublematrix- Returns:
- A
doublescalar value indicating how well the algorithms which have computed the eigenvalue and eigenvector pairs have performed. A performance index less than 1 is considered excellent, 1 to 100 is good, while greater than 100 is considered poor.
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Set the maximum number of iterations allowed.- Parameters:
maxIterations- anintspecifying the maximum number of iterations allowed.maxIterationsmust be greater than 0. By default,maxIterations= 50.
-
solve
public void solve(double[][] a, boolean computeVectors) throws Eigen.DidNotConvergeExceptionSolves for the eigenvalues and (optionally) the eigenvectors of a real square matrix.- Parameters:
a- is thedoublesquare matrix for which the eigenvalues and (optionally) eigenvectors are to be foundcomputeVectors- is true if the eigenvectors are to be computed- Throws:
Eigen.DidNotConvergeException- is thrown when the algorithm fails to converge on the eigenvalues of the matrix.
-
-