- java.lang.Object
-
- com.imsl.math.LU
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class LU extends Object implements Serializable, Cloneable
LU factorization of a matrix of typedouble.LUperforms an LU factorization of a real general coefficient matrix. Theconditionmethod estimates the reciprocal of the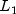 condition number of
the matrix. The LU factorization is done using scaled partial pivoting.
Scaled partial pivoting differs from partial pivoting in that the pivoting
strategy is the same as if each row were scaled to have the same infinity
norm.
condition number of
the matrix. The LU factorization is done using scaled partial pivoting.
Scaled partial pivoting differs from partial pivoting in that the pivoting
strategy is the same as if each row were scaled to have the same infinity
norm.The
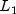 condition number of the matrix
A is defined to be
condition number of the matrix
A is defined to be
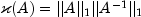 . Since it is expensive
to compute
. Since it is expensive
to compute  , the condition number is only
estimated. The estimation algorithm is the same as used by LINPACK and is
described in a paper by Cline et al. (1979).
, the condition number is only
estimated. The estimation algorithm is the same as used by LINPACK and is
described in a paper by Cline et al. (1979).Note that A is not retained for use by other methods of this class, only the factorization of A is retained. Thus, A is a required parameter to the
conditionmethod.An estimated condition number greater than
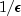 (where
(where  is machine precision) indicates that
very small changes in A can cause very large changes
in the solution x. Iterative refinement can sometimes
find the solution to such a system. If there is conern about the input
matrix being ill-conditioned, the user of this class should check the
condition number of the input matrix using the
is machine precision) indicates that
very small changes in A can cause very large changes
in the solution x. Iterative refinement can sometimes
find the solution to such a system. If there is conern about the input
matrix being ill-conditioned, the user of this class should check the
condition number of the input matrix using the conditionmethod before using one of the other class methods.LUfails if U, the upper triangular part of the factorization, has a zero diagonal element. This can occur only if A either is singular or is very close to a singular matrix.Use the
solvemethod to solve systems of equations. Thedeterminantmethod can be called to compute the determinant of the coefficient matrix.LUis based on the LINPACK routineSGECO; see Dongarra et al. (1979).SGECOuses unscaled partial pivoting.- See Also:
- Example, Serialized Form
-
-
Field Summary
Fields Modifier and Type Field and Description protected double[][]factorThis is an n by n matrix containing the LU factorization of the matrix A.protected int[]ipvtVector of length n containing the pivot sequence for the factorization.
-
Constructor Summary
Constructors Constructor and Description LU(double[][] a)Creates the LU factorization of a square matrix of typedouble.
-
Method Summary
Methods Modifier and Type Method and Description doublecondition(double[][] a)Return an estimate of the reciprocal of the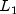 condition number
of a matrix.
condition number
of a matrix.doubledeterminant()Return the determinant of the matrix used to construct this instance.double[][]getL()Returns the lower triangular portion of the LU factorization of A.double[][]getPermutationMatrix()Returns the permutation matrix which results from the LU factorization of A.double[][]getU()Returns the unit upper triangular portion of the LU factorization of A.double[][]inverse()Returns the inverse of the matrix used to construct this instance.double[]solve(double[] b)Return the solution x of the linear system Ax = b using the LU factorization of A.static double[]solve(double[][] a, double[] b)Solve Ax = b for x using the LU factorization of A.double[]solveTranspose(double[] b)Return the solution x of the linear system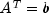 .
.
-
-
-
Field Detail
-
factor
protected double[][] factor
This is an n by n matrix containing the LU factorization of the matrix A.
-
ipvt
protected int[] ipvt
Vector of length n containing the pivot sequence for the factorization.
-
-
Constructor Detail
-
LU
public LU(double[][] a) throws SingularMatrixException
Creates the LU factorization of a square matrix of typedouble.- Parameters:
a- thedoublesquare matrix to be factored- Throws:
IllegalArgumentException- is thrown when the row lengths of input matrix are not equal (for example, the matrix edges are "jagged".)SingularMatrixException- is thrown when the input matrix is singular.
-
-
Method Detail
-
condition
public double condition(double[][] a)
Return an estimate of the reciprocal of the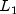 condition number
of a matrix.
condition number
of a matrix.- Parameters:
a- thedoublesquare matrix for which the reciprocal of the condition number is desired
condition number is desired- Returns:
- a
doublevalue representing an estimate of the reciprocal of the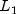 condition number of the matrix
condition number of the matrix
-
determinant
public double determinant()
Return the determinant of the matrix used to construct this instance.- Returns:
- a
doublescalar containing the determinant of the matrix used to construct this instance
-
getL
public double[][] getL()
Returns the lower triangular portion of the LU factorization of A.Scaled partial pivoting is used to achieve the LU factorization. The resulting factorization is such that
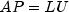 , where A is the input matrix
, where A is the input matrix
a, P is the permutation matrix returned bygetPermutationMatrix, L is the lower triangular matrix returned bygetL, and U is the unit upper triangular matrix returned bygetU.- Returns:
- a
doublematrix containing L, the lower triangular portion of the LU factorization of A.
-
getPermutationMatrix
public double[][] getPermutationMatrix()
Returns the permutation matrix which results from the LU factorization of A.Scaled partial pivoting is used to achieve the LU factorization. The resulting factorization is such that
 , where A is the input matrix
, where A is the input matrix
a, P is the permutation matrix returned bygetPermutationMatrix, L is the lower triangular matrix returned bygetL, and U is the unit upper triangular matrix returned bygetU.- Returns:
- a
doublematrix containing the permuted identity matrix as a result of the LU factorization of A.
-
getU
public double[][] getU()
Returns the unit upper triangular portion of the LU factorization of A.Scaled partial pivoting is used to achieve the LU factorization. The resulting factorization is such that
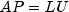 , where A is the input matrix
, where A is the input matrix
a, P is the permutation matrix returned bygetPermutationMatrix, L is the lower triangular matrix returned bygetL, and U is the unit upper triangular matrix returned bygetU.- Returns:
- a
doublematrix containing U, the unit upper triangular portion of the LU factorization of A.
-
inverse
public double[][] inverse()
Returns the inverse of the matrix used to construct this instance.- Returns:
- a
doublematrix representing the inverse of the matrix used to construct this instance
-
solve
public double[] solve(double[] b)
Return the solution x of the linear system Ax = b using the LU factorization of A.- Parameters:
b- adoublearray containing the right-hand side of the linear system- Returns:
- a
doublearray containing the solution to the linear system of equations
-
solve
public static double[] solve(double[][] a, double[] b) throws SingularMatrixExceptionSolve Ax = b for x using the LU factorization of A.- Parameters:
a- adoublesquare matrixb- adoublecolumn vector- Returns:
- a
doublecolumn vector containing the solution to the linear system of equations - Throws:
IllegalArgumentException- This exception is thrown when (1) the lengths of the rows of the input matrix are not uniform, and (2) the number of rows in the input matrix is not equal to the number of elements in x.SingularMatrixException- is thrown when the matrix is singular.
-
solveTranspose
public double[] solveTranspose(double[] b)
Return the solution x of the linear system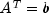 .
.- Parameters:
b-doublearray containing the right-hand side of the linear system- Returns:
doublearray containing the solution to the linear system of equations
-
-