- java.lang.Object
-
- com.imsl.math.NumericalDerivatives
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class NumericalDerivatives extends Object implements Serializable, Cloneable
Compute the Jacobian matrix for a function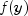 with
m components in n independent variables.
with
m components in n independent variables.
NumericalDerivativesuses divided finite differences to compute the Jacobian. This class is designed for use in numerical methods for solving nonlinear problems where a Jacobian is evaluated repeatedly at neighboring arguments. For example this occurs in a Gauss-Newton method for solving non-linear least squares problems or a non-linear optimization method.NumericalDerivativesis suited for applications where the Jacobian is a dense matrix. All cases ,
,
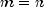 , or
, or 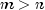 are allowed.
Both one-sided and central divided differences can be used.
are allowed.
Both one-sided and central divided differences can be used.The design allows for computation of derivatives in a variety of contexts. Note that a gradient should be considered as the special case with
 ,
, 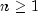 . A derivative of a
single function of one variable is the case
. A derivative of a
single function of one variable is the case 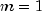 ,
,
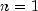 . Any non-linear solving routine that optionally
requests a Jacobian or gradient can use
. Any non-linear solving routine that optionally
requests a Jacobian or gradient can use NumericalDerivatives. This should be considered if there are special properties or scaling issues associated with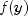 . Use the method
. Use the method
setDifferencingMethodsto specify different differencing options for numerical differentiation. These can be combined with some analytic subexpressions or other known relationships.The divided differences are computed using values of the independent variables at the initial point
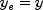 , and differenced
points
, and differenced
points 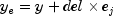 . Here the
. Here the
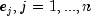 , are the unit coordinate vectors.
The value for each difference del depends on the variable j,
the differencing method, and the scaling for that variable. This difference
is computed internally. See
, are the unit coordinate vectors.
The value for each difference del depends on the variable j,
the differencing method, and the scaling for that variable. This difference
is computed internally. See setPercentageFactorfor computational details. The evaluation of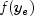 is
normally done by the user-provided method
is
normally done by the user-provided method NumericalDerivatives.Function.f, using the values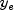 . The index j and values
. The index j and values
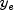 are arguments to
are arguments to NumericalDerivatives.Function.f.The computational kernel of
evaluateJperforms the following steps:- evaluate the equations at the point
yusingNumericalDerivatives.Function.f. - compute the Jacobian.
- compute the difference at
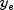 .
.
By default,
evaluateJusesNumericalDerivatives.Function.fin step 3. The user may choose to override theevaluateFmethod to extend the capability of the class beyond the default.There are six examples provided which illustrate various ways to use
NumericalDerivatives. A discussion of the expected errors for these difference methods is found in A First Course in Numerical Analysis, Anthony Ralston, McGraw-Hill, NY, (1965).
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceNumericalDerivatives.FunctionPublic interface function.static interfaceNumericalDerivatives.JacobianPublic interface for the user-supplied function to compute the Jacobian.
-
Field Summary
Fields Modifier and Type Field and Description static intACCUMULATEIndicates the accumulation of the result from whatever type of differences have been specified previously into initial values of the Jacobian.static intCENTRALIndicates central differences.static intONE_SIDEDIndicates one sided differences.static intSKIPIndicates a variable to be skipped.
-
Constructor Summary
Constructors Constructor and Description NumericalDerivatives(NumericalDerivatives.Function fcn)Constructor forNumericalDerivatives.
-
Method Summary
Methods Modifier and Type Method and Description protected double[]evaluateF(int varIndex, double[] y)This method is provided by the user to compute the function values at the current independent variable valuesy.double[][]evaluateJ(double[] y)Evaluates the Jacobian for a system of (m) equations in (n) variables.double[]getPercentageFactor()Returns the percentage factor for differencing.double[]getScalingFactors()Returns the scaling factors for theyvalues.int[]getStatus()Returns status information.voidsetDifferencingMethods(int[] options)Sets the methods used to compute the derivativesvoidsetInitialF(double[] valueF)Set the initial function values.voidsetPercentageFactor(double[] factor)Sets the percentage factor for differencingvoidsetScalingFactors(double[] scale)Sets the scaling factors for theyvalues.
-
-
-
Field Detail
-
ACCUMULATE
public static final int ACCUMULATE
Indicates the accumulation of the result from whatever type of differences have been specified previously into initial values of the Jacobian.- See Also:
- Constant Field Values
-
CENTRAL
public static final int CENTRAL
Indicates central differences.- See Also:
- Constant Field Values
-
ONE_SIDED
public static final int ONE_SIDED
Indicates one sided differences.- See Also:
- Constant Field Values
-
SKIP
public static final int SKIP
Indicates a variable to be skipped.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
NumericalDerivatives
public NumericalDerivatives(NumericalDerivatives.Function fcn)
Constructor forNumericalDerivatives.- Parameters:
fcn- aFunctionobject which is a user-supplied function to evaluate the equations at the pointy.
-
-
Method Detail
-
evaluateF
protected double[] evaluateF(int varIndex, double[] y)This method is provided by the user to compute the function values at the current independent variable valuesy. If the user does not override theevaluateFmethod, thenNumericalDerivatives.Function.fis used to compute the function values.- Parameters:
varIndex- anintwhich indicates the index of the variable to perturb.y- adoublearray of length n, the point at which the function is to be evaluated.- Returns:
- a
doublearray of length m. The equations evaluated at the pointy.
-
evaluateJ
public double[][] evaluateJ(double[] y)
Evaluates the Jacobian for a system of (m) equations in (n) variables.- Parameters:
y- adoublearray of length n, the point at which the Jacobian is to be evaluated.- Returns:
- a
doublematrix containing the Jacobian. Columns that are accumulated must have the additive term defined on entry or else be set to zero. Columns that are skipped can be defined either before or after theevaluateJmethod is invoked.
-
getPercentageFactor
public double[] getPercentageFactor()
Returns the percentage factor for differencing.- Returns:
- a
doublearray containing the percentage factor for differencing. SeesetPercentageFactorfor more detail.
-
getScalingFactors
public double[] getScalingFactors()
Returns the scaling factors for theyvalues.- Returns:
- a
doublearray containing the scaling factors.
-
getStatus
public int[] getStatus()
Returns status information. This information might prove useful to the user wanting to gain better control over the differencing parameters. This information can often be ignored.- Returns:
- an
intarray containing the ten diagnostic values described in the following table. These values can be used to monitor the progress or expense of the Jacobian computation.index Description 0 the number of times a function evaluation was computed. 1 the number of columns in which three attempts were made to increase a percentage factor for differencing (i.e. a component in the factorarray) but the computed del remained unacceptably small relative toy[j-1]orscale[j-1]. In such cases the percentage factor is set to 1.4901161193847656e-8, which is the square root of machine precision2 the number of columns in which the computed del was zero to machine precision because y[j-1]orscale[j-1]was zero. In such cases del is set to 1.4901161193847656e-8, which is the square root of machine precision3 the number of Jacobian columns which had to be recomputed because the largest difference formed in the column was close to zero relative to scale, where
and i denotes the row index of the largest difference in the column currently being processed. index = 9 gives the last column where this occurred.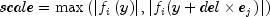
4 the number of columns whose largest difference is close to zero relative to scale after the column has been recomputed. 5 the number of times scale information was not available for use in the roundoff and truncation error tests. This occurs when
where i is the index of the largest difference for the column currently being processed.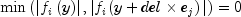
6 the number of times the increment for differencing (del) was computed and had to be increased because ( scale[j-1]+del) -scale[j-1]) was too small relative toy[j-1]orscale[j-1].7 the number of times a component of the factorarray was reduced because changes in function values were large and excess truncation error was suspected. index = 8 gives the last column in which this occurred.8 the index of the last column where the corresponding component of the factorarray had to be reduced because excessive truncation error was suspected.9 the index of the last column where the difference was small and the column had to be recomputed with an adjusted increment (see index = 3). The largest derivative in this column may be inaccurate due to excessive roundoff error.
-
setDifferencingMethods
public void setDifferencingMethods(int[] options)
Sets the methods used to compute the derivatives- Parameters:
options- anintarray of length n, containing the methods used to compute the derivatives.options[i]is the method to be used for the i-th variable.options[i]can be one of the values in the table which follows. The default is to useONE_SIDEDdifferences for each variable.Entry Description ONE_SIDEDIndicates one sided differences. CENTRALIndicates central differences. ACCUMULATEIndicates the accumulation of the result from whatever type of differences have been specified previously into initial values of the Jacobian. SKIPIndicates a variable to be skipped.
-
setInitialF
public void setInitialF(double[] valueF)
Set the initial function values. Use the values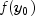 , where
, where 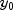 is the
initial value of the independent variables located in array
is the
initial value of the independent variables located in array y.- Parameters:
valueF- adoublearray of length m containing the initial function values,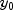 . Default: all values are
0.0.
. Default: all values are
0.0.
-
setPercentageFactor
public void setPercentageFactor(double[] factor)
Sets the percentage factor for differencingFor each divided difference for variable j the increment used is del. The value of del is computed as follows: First define
![sigma = sign(mbox{scale}[j - 1])](eqn_0993.png) . If the
user has set the elements of array
. If the
user has set the elements of array scaleto non-default values, then define![y_a = left| {mbox{scale}[j - 1]} right|](eqn_0994.png) .
Otherwise
.
Otherwise ![y_a = left| {y[j - 1]} right|](eqn_0995.png) and
and
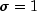 . Finally compute
. Finally compute
![del=sigma y{}_a;mbox{factor}[j-1]](eqn_0997.png) . By changing
the sign of
. By changing
the sign of scale[j-1], the difference del can have any desired orientation, such as staying within bounds on variable j. For central differences, a reduced factor is used for del that normally results in relative errors as small as machine precision to the 2/3 power.- Parameters:
factor- adoublearray of length n containing the percentage factor for differencing. Except for initialization, thefactorarray should not be altered in theevaluateFmethod. The elements offactormust be such that
where 1.8189894035458565e-12 is machine precision to the three-fourths power.![mbox{1.8189894035458565e-12};lembox{factor}[j-1]le 0.1](eqn_0998.png)
Default: all elements offactorare set to 1.4901161193847656e-8, which is the square root of machine precision.
-
setScalingFactors
public void setScalingFactors(double[] scale)
Sets the scaling factors for theyvalues. The user can also usescaleto provide appropriate signs for the increments.- Parameters:
scale- adoublearray of length n containing the scaling factors. Default: all values are 1.0.
-
-