- java.lang.Object
-
- com.imsl.math.QR
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class QR extends Object implements Serializable, Cloneable
QR Decomposition of a matrix.Class
QRcomputes the QR decomposition of a matrix using Householder transformations. It is based on the LINPACK routineSQRDC; see Dongarra et al. (1979).QRdetermines an orthogonal matrix Q, a permutation matrix P, and an upper trapezoidal matrix R with diagonal elements of nonincreasing magnitude, such that AP = QR. The Householder transformation for column k is of the form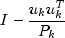
for
 , min(number of rows of A, number
of columns of A), where u has zeros in the first
k - 1 positions. The matrix Q is
not produced directly by
, min(number of rows of A, number
of columns of A), where u has zeros in the first
k - 1 positions. The matrix Q is
not produced directly by QR. Instead the information needed to reconstruct the Householder transformations is saved. If the matrix Q is needed explicitly, the methodgetQcan be called afterQR. This method accumulates Q from its factored form.Before the decomposition is computed, initial columns are moved to the beginning of the array A and the final columns to the end. Both initial and final columns are frozen in place during the computation. Only free columns are pivoted. Pivoting is done on the free columns of largest reduced norm.
- See Also:
- Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description QR(double[][] a)Constructs the QR decomposition of a matrix with elements of typedouble.
-
Method Summary
Methods Modifier and Type Method and Description int[]getPermute()Returns an integer vector containing information about the permutation of the elements of the matrix during pivoting.double[][]getQ()Returns the orthogonal or unitary matrix Q.double[][]getR()Returns the upper trapezoidal matrix R.intgetRank()Returns the rank of the matrix used to construct this instance.intrank(double tolerance)Returns the rank of the matrix given an input tolerance.double[]solve(double[] b)Returns the solution to the least-squares problem Ax = b.double[]solve(double[] b, double tol)Returns the solution to the least-squares problem Ax = b using an input tolerance.
-
-
-
Constructor Detail
-
QR
public QR(double[][] a)
Constructs the QR decomposition of a matrix with elements of typedouble.- Parameters:
a- adoublematrix to be factored- Throws:
IllegalArgumentException- Thrown when the row lengths of input matrix a are not equal (i.e. the matrix edges are "jagged".)
-
-
Method Detail
-
getPermute
public int[] getPermute()
Returns an integer vector containing information about the permutation of the elements of the matrix during pivoting.- Returns:
- an
intarray containing the permutation information. The k-th element contains the index of the column of the matrix that has been interchanged into the k-th column.
-
getQ
public double[][] getQ()
Returns the orthogonal or unitary matrix Q.- Returns:
- a
doublematrix containing the accumulated orthogonal matrix Q from the QR decomposition
-
getR
public double[][] getR()
Returns the upper trapezoidal matrix R.- Returns:
- the upper trapezoidal
doublematrix R of the QR decomposition
-
getRank
public int getRank()
Returns the rank of the matrix used to construct this instance.- Returns:
- an
intspecifying the rank of the matrix used to construct this instance
-
rank
public int rank(double tolerance)
Returns the rank of the matrix given an input tolerance.- Parameters:
tolerance- adoublescalar value used in determining the rank of the matrix- Returns:
- an
intspecifying the rank of the matrix
-
solve
public double[] solve(double[] b) throws SingularMatrixExceptionReturns the solution to the least-squares problem Ax = b.- Parameters:
b- adoublearray to be manipulated- Returns:
- a
doublearray containing the solution vector to Ax = b with components corresponding to the unused columns set to zero - Throws:
SingularMatrixException- Thrown when the upper triangular matrix R resulting from the QR factorization is singular.
-
solve
public double[] solve(double[] b, double tol) throws SingularMatrixExceptionReturns the solution to the least-squares problem Ax = b using an input tolerance.- Parameters:
b- adoublearray to be manipulatedtol- adoublescalar value used in determining the rank of A- Returns:
- a
doublearray containing the solution vector to Ax = b with components corresponding to the unused columns set to zero - Throws:
SingularMatrixException- Thrown when the upper triangular matrix R resulting from the QR factorization is singular.
-
-