- java.lang.Object
-
- com.imsl.math.SVD
-
public class SVD extends Object
Singular Value Decomposition (SVD) of a rectangular matrix of typedouble.SVDis based on the LINPACK routineSSVDC; see Dongarra et al. (1979).Let n be the number of rows in A and let p be the number of columns in A. For any
n x p matrix A, there exists an n x n orthogonal matrix U and a p x p orthogonal matrix V such that![U^T A V = left{ begin{array}{cl} left[
begin{array}{l} Sigma \ 0 end{array} right] & mbox{if n ge p } \
left[ Sigma ,, 0 right] & mbox{if n le p } end{array} right.](eqn_0615.png)
where
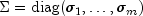 , and
, and
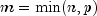 . The scalars
. The scalars  are called the
singular values of A. The columns of U
are called the left singular vectors of A. The
columns of V are called the right singular vectors of
A.
are called the
singular values of A. The columns of U
are called the left singular vectors of A. The
columns of V are called the right singular vectors of
A.The estimated rank of A is the number of
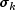 that is larger than a tolerance
that is larger than a tolerance 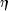 .
If
.
If  is the parameter
is the parameter tolin the program, then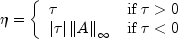
The Moore-Penrose generalized inverse of the matrix is computed by partitioning the matrices U, V and
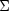 as
as
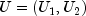 ,
,
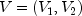 and
and
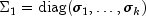 where the "1" matrices are k by k.
The Moore-Penrose generalized inverse is
where the "1" matrices are k by k.
The Moore-Penrose generalized inverse is
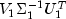 .
.- See Also:
- Example
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classSVD.DidNotConvergeExceptionThe iteration did not converge
-
Constructor Summary
Constructors Constructor and Description SVD(double[][] a)Construct the singular value decomposition of a rectangular matrix with default tolerance.SVD(double[][] a, double tol)Construct the singular value decomposition of a rectangular matrix with a given tolerance.
-
Method Summary
Methods Modifier and Type Method and Description intgetInfo()Returns convergence information about S, U, and V.intgetRank()Returns the rank of the matrix used to construct this instance.double[]getS()Returns the singular values.double[][]getU()Returns the left singular vectors.double[][]getV()Returns the right singular vectors.double[][]inverse()Compute the Moore-Penrose generalized inverse of a real matrix.
-
-
-
Constructor Detail
-
SVD
public SVD(double[][] a) throws SVD.DidNotConvergeExceptionConstruct the singular value decomposition of a rectangular matrix with default tolerance. The tolerance used is 2.2204460492503e-14. This tolerance is used to determine rank. A singular value is considered negligible if the singular value is less than or equal to this tolerance.- Parameters:
a- adoublematrix for which the singular value decomposition is to be computed- Throws:
IllegalArgumentException- is thrown when the row lengths of input matrix a are not equal (i.e. the matrix edges are "jagged")SVD.DidNotConvergeException
-
SVD
public SVD(double[][] a, double tol) throws SVD.DidNotConvergeExceptionConstruct the singular value decomposition of a rectangular matrix with a given tolerance. Iftolis positive, then a singular value is considered negligible if the singular value is less than or equal totol. Iftolis negative, then a singular value is considered negligible if the singular value is less than or equal to the absolute value of the product oftoland the infinity norm of the input matrix. In the latter case, the absolute value oftolgenerally contains an estimate of the level of the relative error in the data.- Parameters:
a- adoublematrix for which the singular value decomposition is to be computedtol- adoublescalar containing the tolerance used to determine when a singular value is negligible- Throws:
IllegalArgumentException- is thrown when the row lengths of input matrix a are not equal (for example, the matrix edges are "jagged")SVD.DidNotConvergeException- is thrown when the rank cannot be determined because convergence was not obtained for all singular values
-
-
Method Detail
-
getInfo
public int getInfo()
Returns convergence information about S, U, and V.- Returns:
- Convergence was obtained for the info, info+1, ..., min(nra,nca) singular values and their corresponding vectors. Here, nra and nca represent the number of rows and columns of the input matrix respectively.
-
getRank
public int getRank()
Returns the rank of the matrix used to construct this instance.- Returns:
- an
intscalar containing the rank of the matrix used to construct this instance. The estimated rank of the input matrix is the number of singular values which are larger than a tolerance.
-
getS
public double[] getS()
Returns the singular values.- Returns:
- a
doublearray containing the singular values of the matrix
-
getU
public double[][] getU()
Returns the left singular vectors.- Returns:
- a
doublematrix containing the left singular vectors
-
getV
public double[][] getV()
Returns the right singular vectors.- Returns:
- a
doublematrix containing the right singular vectors
-
inverse
public double[][] inverse()
Compute the Moore-Penrose generalized inverse of a real matrix.- Returns:
- a
doublematrix containing the generalized inverse of the matrix used to construct this instance
-
-