- java.lang.Object
-
- com.imsl.math.SparseLP
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class SparseLP extends Object implements Serializable, Cloneable
Solves a sparse linear programming problem by an infeasible primal-dual interior-point method.Class
SparseLPuses an infeasible primal-dual interior-point method to solve linear programming problems, i.e., problems of the form
where c is the objective coefficient vector, A is the coefficient matrix, and the vectors
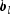 ,
, 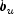 ,
, 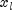 ,
and
,
and  are the lower and upper bounds on the
constraints and the variables, respectively.
are the lower and upper bounds on the
constraints and the variables, respectively.Internally,
SparseLPtransforms the problem given by the user into a simpler form that is computationally more tractable. After redefining the notation, the new form reads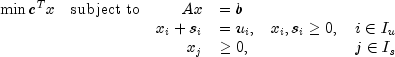
Here,
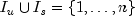 is a partition of
the index set
is a partition of
the index set  into upper bounded and
standard variables.
into upper bounded and
standard variables.In order to simplify the description it is assumed in the following that the problem above contains only variables with upper bounds, i.e. is of the form

The corresponding dual problem is
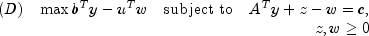
The Karush-Kuhn-Tucker (KKT) optimality conditions for (P) and (D) are
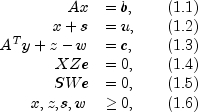
where
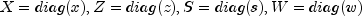 are
diagonal matrices and
are
diagonal matrices and  is a vector of
ones.
is a vector of
ones.Class
SparseLP, like all infeasible interior-point methods, generates a sequence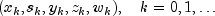
of iterates that satisfy
 for all
k, but are in general not feasible, i.e. the linear constraints
(1.1)-(1.3) are only satisfied in the limiting case
for all
k, but are in general not feasible, i.e. the linear constraints
(1.1)-(1.3) are only satisfied in the limiting case
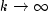 .
.The barrier parameter
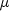 , defined by
, defined by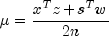
measures how good the complementarity conditions (1.4), (1.5) are satisfied.
Mehrotra's predictor-corrector algorithm is a variant of Newton's method applied to the KKT conditions (1.1)-(1.5). Class
SparseLPuses a modified version of this algorithm to compute the iterates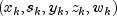 . In every step of the algorithm,
the search direction vector
. In every step of the algorithm,
the search direction vector
is decomposed into two parts,
 , where
, where
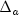 and
and  denote the affine-scaling and the weighted centering components, respectively.
Here,
denote the affine-scaling and the weighted centering components, respectively.
Here,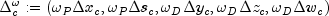
where
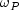 and
and 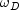 denote the primal and dual corrector weights, respectively.
denote the primal and dual corrector weights, respectively.The vectors
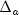 and
and
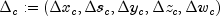 are determined by solving the linear system
are determined by solving the linear system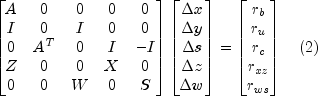
for two different right-hand sides.
For
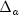 , the right-hand side is defined as
, the right-hand side is defined as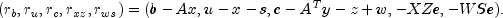
Here,
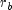 and
and 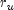 are the
violations of the primal constraints and
are the
violations of the primal constraints and 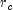 defines the
violations of the dual constraints.
defines the
violations of the dual constraints.The resulting direction
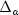 is the pure Newton step
applied to the system (1.1)-(1.5).
is the pure Newton step
applied to the system (1.1)-(1.5).In order to obtain the corrector direction
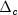 , the
maximum stepsizes
, the
maximum stepsizes 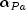 in the primal and
in the primal and
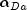 in the dual space preserving nonnegativity
of
in the dual space preserving nonnegativity
of 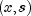 and
and 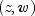 respectively,
are determined, and the predicted complementarity gap
respectively,
are determined, and the predicted complementarity gap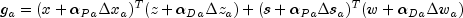
is computed. It is then used to determine the barrier parameter
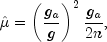
where
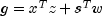 denotes the current complementarity
gap.
denotes the current complementarity
gap.The direction
 is then computed by choosing
is then computed by choosing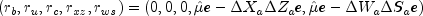
as the right-hand side in the linear system (2).
Class
SparseLPnow uses a line search to find the optimal weight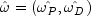 that maximizes the stepsizes
that maximizes the stepsizes  in the primal and dual directions of
in the primal and dual directions of
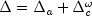 , respectively.
, respectively.A new iterate is then computed using a step reduction factor
 :
: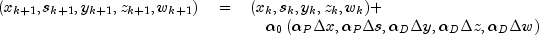
In addition to the weighted Mehrotra predictor-corrector,
SparseLPalso uses multiple centrality correctors to enlarge the primal-dual stepsizes per iteration step and to reduce the overall number of iterations required to solve an LP problem. The maximum number of centrality corrections depends on the ratio of the factorization and solve efforts for system (2) and is therefore problem dependent. For a detailed description of multiple centrality correctors, refer to Gondzio (1994).The linear system (2) can be reduced to more compact forms, the augmented system (AS)
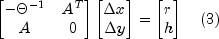
or further by elimination of
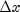 to the normal equations (NE)
system
to the normal equations (NE)
system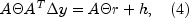
where
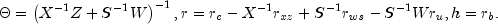
The matrix on the left-hand side of (3), which is symmetric indefinite, can be transformed into a symmetric quasidefinite matrix by regularization. Since these types of matrices allow for a Cholesky-like factorization, the resulting linear system can be solved easily for
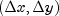 by triangular substitutions. For
more information on the regularization technique, see Altman and Gondzio
(1998). For the NE system, matrix
by triangular substitutions. For
more information on the regularization technique, see Altman and Gondzio
(1998). For the NE system, matrix 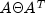 is positive definite, and therefore a sparse Cholesky algorithm can be used
to factor
is positive definite, and therefore a sparse Cholesky algorithm can be used
to factor  and solve the system for
and solve the system for
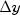 by triangular substitutions with the Cholesky
factor L.
by triangular substitutions with the Cholesky
factor L.In class
SparseLP, both approaches are implemented. The AS approach is chosen if A contains dense columns, if there are a considerable number of columns in A that are much denser than the remaining ones, or if there are many more rows than columns in the structural part of A. Otherwise, the NE approach is selected.Class
SparseLPstops with optimal termination status if the current iterate satisfies the following three conditions: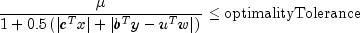
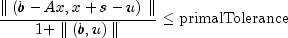
and
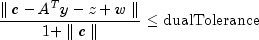
where
primalTolerance,dualToleranceandoptimalityToleranceare primal infeasibility, dual infeasibility and optimality tolerances, respectively. The default value is 1.0e-10 foroptimalityToleranceand 1.0e-8 for the other two tolerances.Class
SparseLPis based on the code HOPDM developed by Jacek Gondzio et al., see the HOPDM User's Guide (1995).- See Also:
- Example 1, Example 2, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classSparseLP.CholeskyFactorizationAccuracyExceptionThe Cholesky factorization failed because of accuracy problems.static classSparseLP.DiagonalWeightMatrixExceptionA diagonal element of the diagonal weight matrix is too small.static classSparseLP.DualInfeasibleExceptionThe dual problem is infeasible.static classSparseLP.IllegalBoundsExceptionThe lower bound is greater than the upper bound.static classSparseLP.IncorrectlyActiveExceptionOne or more LP variables are falsely characterized by the internal presolver.static classSparseLP.IncorrectlyEliminatedExceptionOne or more LP variables are falsely characterized by the internal presolver.static classSparseLP.InitialSolutionInfeasibleExceptionThe initial solution for the one-row linear program is infeasible.static classSparseLP.PrimalInfeasibleExceptionThe primal problem is infeasible.static classSparseLP.PrimalUnboundedExceptionThe primal problem is unbounded.static classSparseLP.ProblemUnboundedExceptionThe problem is unbounded.static classSparseLP.TooManyIterationsExceptionThe maximum number of iterations has been exceeded.static classSparseLP.ZeroColumnExceptionA column of the constraint matrix has no entries.static classSparseLP.ZeroRowExceptionA row of the constraint matrix has no entries.
-
Constructor Summary
Constructors Constructor and Description SparseLP(int[] colPtr, int[] rowInd, double[] values, double[] b, double[] c)Constructs aSparseLPobject using Compressed Sparse Column (CSC), or Harwell-Boeing format.SparseLP(MPSReader mps)Constructs aSparseLPobject using anMPSReaderobject.SparseLP(SparseMatrix a, double[] b, double[] c)Constructs aSparseLPobject.
-
Method Summary
Methods Modifier and Type Method and Description doublegetConstant()Returns the value of the constant term in the objective function.int[]getConstraintType()Returns the types of general constraints in the matrix A.doublegetDualInfeasibility()Returns the dual infeasibility of the solution.doublegetDualInfeasibilityTolerance()Returns the dual infeasibility tolerance.double[]getDualSolution()Returns the dual solution.intgetIterationCount()Returns the number of iterations used by the primal-dual solver.doublegetLargestCPRatio()Returns the ratio of the largest complementarity product to the average.double[]getLowerBound()Returns the lower bound on the variables.intgetMaxIterations()Returns the maximum number of iterations allowed for the primal-dual solver.doublegetOptimalValue()Returns the optimal value of the objective function.intgetPreordering()Returns the variant of the Minimum Degree Ordering (MDO) algorithm used in the preordering of the normal equations or augmented system matrix.intgetPresolve()Returns the presolve option.doublegetPrimalInfeasibility()Returns the primal infeasibility of the solution.doublegetPrimalInfeasibilityTolerance()Returns the primal infeasibility tolerance.intgetPrintLevel()Returns the print level.doublegetRelativeOptimalityTolerance()Returns the relative optimality tolerance.doublegetSmallestCPRatio()Returns the ratio of the smallest complementarity product to the average.double[]getSolution()Returns the solution x of the linear programming problem.intgetTerminationStatus()Returns the termination status for the problem.double[]getUpperBound()Returns the upper bound on the variables.double[]getUpperLimit()Returns the upper limit of the constraints that have both a lower and an upper bound.doublegetViolation()Returns the violation of the variable bounds.voidsetConstant(double c0)Sets the value of the constant term in the objective function.voidsetConstraintType(int[] constraintType)Sets the types of general constraints in the matrix A.voidsetDualInfeasibilityTolerance(double dualTolerance)Sets the dual infeasibility tolerance.voidsetLowerBound(double[] lowerBound)Sets the lower bound on the variables.voidsetMaxIterations(int maxIterations)Sets the maximum number of iterations allowed for the primal-dual solver.voidsetPreordering(int preorder)Sets the variant of the Minimum Degree Ordering (MDO) algorithm used in the preordering of the normal equations or augmented system matrix.voidsetPresolve(int presolve)Sets the presolve option.voidsetPrimalInfeasibilityTolerance(double primalTolerance)Sets the primal infeasibility tolerance.voidsetPrintLevel(int printLevel)Sets the print level.voidsetRelativeOptimalityTolerance(double optimalityTolerance)Sets the relative optimality tolerance.voidsetUpperBound(double[] upperBound)Sets the upper bound on the variables.voidsetUpperLimit(double[] bu)Sets the upper limit of the constraints that have both a lower and an upper bound.voidsolve()Solves the sparse linear programming problem by an infeasible primal-dual interior-point method.
-
-
-
Constructor Detail
-
SparseLP
public SparseLP(int[] colPtr, int[] rowInd, double[] values, double[] b, double[] c)Constructs aSparseLPobject using Compressed Sparse Column (CSC), or Harwell-Boeing format. See Compressed Sparse Column (CSC) Format, Chapter 1.- Parameters:
colPtr- anintarray containing the location invaluesin which to place the first nonzero value of each succeeding column of the constraint matrix A.colPtr,rowIndandvaluesspecify the location and value of each nonzero coefficient in the constraint matrix A in CSC format.rowInd- anintarray containing a list of the row indices of each column of the constraint matrix A.colPtr,rowIndandvaluesspecify the location and value of each nonzero coefficient in the constraint matrix A in CSC format.values- adoublearray containing the value of each nonzero coefficient in the constraint matrix A.colPtr,rowIndandvaluesspecify the location and value of each nonzero coefficient in the constraint matrix A in CSC format.b- adoublearray of length m, number of constraints, containing the right-hand side of the constraints; if there are limits on both sides of the constraints, thenbcontains the lower limit of the constraintsc- adoublearray of length n, the number of variables, containing the coefficients of the objective function
-
SparseLP
public SparseLP(MPSReader mps)
Constructs aSparseLPobject using anMPSReaderobject.- Parameters:
mps- anMPSReaderobject specifying the Linear Programming problem
-
SparseLP
public SparseLP(SparseMatrix a, double[] b, double[] c)
Constructs aSparseLPobject.- Parameters:
a- aSparseMatrixobject containing the location and value of each nonzero coefficient in the constraint matrix A. If there is no constraint matrix, seta = null.b- adoublearray of length m, the number of constraints, containing the right-hand side of the constraints. If there are limits on both sides of the constraints, thenbcontains the lower limit of the constraints.c- adoublearray of length n, the number of variables, containing the coefficients of the objective function
-
-
Method Detail
-
getConstant
public double getConstant()
Returns the value of the constant term in the objective function.- Returns:
- a
doublescalar containing the value of the constant term in the objective function
-
getConstraintType
public int[] getConstraintType()
Returns the types of general constraints in the matrix A. SeesetConstraintType.- Returns:
- an
intarray containing the types of general constraints in the matrix A
-
getDualInfeasibility
public double getDualInfeasibility()
Returns the dual infeasibility of the solution.- Returns:
- a
doublescalar containing the dual infeasibility of the solution,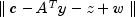
-
getDualInfeasibilityTolerance
public double getDualInfeasibilityTolerance()
Returns the dual infeasibility tolerance.- Returns:
- a
doublescalar containing the dual infeasibility tolerance
-
getDualSolution
public double[] getDualSolution()
Returns the dual solution.- Returns:
- a
doublearray containing the dual solution
-
getIterationCount
public int getIterationCount()
Returns the number of iterations used by the primal-dual solver.- Returns:
- an
intscalar containing the number of iterations used by the primal-dual solver
-
getLargestCPRatio
public double getLargestCPRatio()
Returns the ratio of the largest complementarity product to the average.- Returns:
- a
doublescalar containing the ratio of the largest complementarity product to the average
-
getLowerBound
public double[] getLowerBound()
Returns the lower bound on the variables.- Returns:
- a
doublearray containing the lower bound on the variables
-
getMaxIterations
public int getMaxIterations()
Returns the maximum number of iterations allowed for the primal-dual solver.- Returns:
- an
intscalar containing the maximum number of iterations allowed for the primal-dual solver
-
getOptimalValue
public double getOptimalValue()
Returns the optimal value of the objective function.- Returns:
- a
doublescalar containing the optimal value of the objective function
-
getPreordering
public int getPreordering()
Returns the variant of the Minimum Degree Ordering (MDO) algorithm used in the preordering of the normal equations or augmented system matrix. SeesetPreordering.- Returns:
- an
intscalar containing the variant of the Minimum Degree Ordering (MDO) algorithm used in the preordering of the normal equations or augmented system matrix
-
getPresolve
public int getPresolve()
Returns the presolve option. SeesetPresolve.- Returns:
- an
intscalar containing the presolve option
-
getPrimalInfeasibility
public double getPrimalInfeasibility()
Returns the primal infeasibility of the solution.- Returns:
- a
doublescalar containing the primal infeasibility of the solution,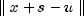
-
getPrimalInfeasibilityTolerance
public double getPrimalInfeasibilityTolerance()
Returns the primal infeasibility tolerance.- Returns:
- a
doublescalar containing the primal infeasibility tolerance
-
getPrintLevel
public int getPrintLevel()
Returns the print level. SeesetPrintLevel.- Returns:
- an
intscalar containing the print level
-
getRelativeOptimalityTolerance
public double getRelativeOptimalityTolerance()
Returns the relative optimality tolerance.- Returns:
- a
doublescalar containing the relative optimality tolerance
-
getSmallestCPRatio
public double getSmallestCPRatio()
Returns the ratio of the smallest complementarity product to the average.- Returns:
- a
doublescalar containing the ratio of the smallest complementarity product to the average
-
getSolution
public double[] getSolution()
Returns the solution x of the linear programming problem.- Returns:
- a
doublearray containing the solution x of the linear programming problem
-
getTerminationStatus
public int getTerminationStatus()
Returns the termination status for the problem.- Returns:
- an
intscalar containing the termination status for the problemstatus
Description
0 Optimal solution found. 1 The problem is primal infeasible (or dual unbounded). 2 The problem is primal unbounded (or dual infeasible). 3 Suboptimal solution found (accuracy problems). 4 Iterations limit maxIterationsexceeded.5 An error outside of the solution phase of the algorithm, e.g. a user input or a memory allocation error.
-
getUpperBound
public double[] getUpperBound()
Returns the upper bound on the variables.- Returns:
- a
doublearray containing the upper bound on the variables
-
getUpperLimit
public double[] getUpperLimit()
Returns the upper limit of the constraints that have both a lower and an upper bound.- Returns:
- a
doublearray containing the upper limit of the constraints that have both a lower and an upper bound. Returnsnullif the upper limit has not been set.
-
getViolation
public double getViolation()
Returns the violation of the variable bounds.- Returns:
- a
doublescalar containing the violation of the variable bounds,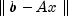
-
setConstant
public void setConstant(double c0)
Sets the value of the constant term in the objective function.- Parameters:
c0- adoublescalar containing the value of the constant term in the objective functionDefault:
c0 = 0
-
setConstraintType
public void setConstraintType(int[] constraintType)
Sets the types of general constraints in the matrix A.- Parameters:
constraintType- anintarray of length m containing the types of general constraints in the matrix A. Let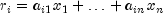 . Then, the
value of
. Then, the
value of constraintType[i]signifies the following:constraintType
Constraint
0 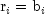
1 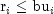
2 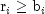
3 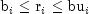
4 Ignore this constraint
Note that
constraintType[i] = 3should only be used for constraintsiwith both a finite lower and a finite upper bound. For one-sided constraints, useconstraintType[i] = 1orconstraintType[i] = 2. For free constraints, useconstraintType[i] = 4.Default:
constraintType[i] = 0
-
setDualInfeasibilityTolerance
public void setDualInfeasibilityTolerance(double dualTolerance)
Sets the dual infeasibility tolerance.- Parameters:
dualTolerance- adoublescalar containing the dual infeasibility toleranceDefault:
dualTolerance = 1.0e-8
-
setLowerBound
public void setLowerBound(double[] lowerBound)
Sets the lower bound on the variables.- Parameters:
lowerBound- adoublearray of length n containing the lower bound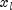 on the variables. If
there is no lower bound on a variable, then -1.0e30 should be set as the
lower bound.
on the variables. If
there is no lower bound on a variable, then -1.0e30 should be set as the
lower bound.
Default:
lowerBound[i] = 0
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Sets the maximum number of iterations allowed for the primal-dual solver.- Parameters:
maxIterations- anintscalar containing the maximum number of iterations allowed for the primal-dual solverDefault:
maxIterations = 200
-
setPreordering
public void setPreordering(int preorder)
Sets the variant of the Minimum Degree Ordering (MDO) algorithm used in the preordering of the normal equations or augmented system matrix.- Parameters:
preorder- anintscalar containing the variant of the Minimum Degree Ordering (MDO) algorithm used in the preordering of the normal equations or augmented system matrixpreorder Method 0 A variant of the MDO algorithm using pivotal cliques. 1 A variant of George and Liu's Quotient Minimum Degree algorithm.
Default:
preorder = 0
-
setPresolve
public void setPresolve(int presolve)
Sets the presolve option.- Parameters:
presolve- anintcontaining the the presolve option to resolve the LP problem in order to reduce the problem size or to detect infeasibility or unboundedness of the problem. Depending on the number of presolve techniques used, different presolve levels can be chosen:presolve Description 0 No presolving. 1 Eliminate singleton rows. 2 In addition to 1, eliminate redundant (and forcing) rows. 3 In addition to 1 and 2, eliminate dominated variables. 4 In addition to 1, 2, and 3, eliminate singleton columns. 5 In addition to 1, 2, 3, and 4, eliminate doubleton rows. 6 In addition to 1, 2, 3, 4, and 5, eliminate aggregate columns. Default:
presolve = 0
-
setPrimalInfeasibilityTolerance
public void setPrimalInfeasibilityTolerance(double primalTolerance)
Sets the primal infeasibility tolerance.- Parameters:
primalTolerance- adoublescalar containing the primal infeasibility toleranceDefault:
primalTolerance = 1.0e-8
-
setPrintLevel
public void setPrintLevel(int printLevel)
Sets the print level.- Parameters:
printLevel- anintcontaining the print levelprintLevel Action 0 No printing. 1 Prints statistics on the LP problem and the solution process. Default:
printLevel = 0
-
setRelativeOptimalityTolerance
public void setRelativeOptimalityTolerance(double optimalityTolerance)
Sets the relative optimality tolerance.- Parameters:
optimalityTolerance- adoublescalar containing the relative optimality toleranceDefault:
optimalityTolerance = 1.0e-10
-
setUpperBound
public void setUpperBound(double[] upperBound)
Sets the upper bound on the variables.- Parameters:
upperBound- adoublearray of length n containing the upper bound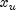 on the variables. If
there is no upper bound on a variable, then 1.0e30 should be set as the
upper bound.
on the variables. If
there is no upper bound on a variable, then 1.0e30 should be set as the
upper bound.
Default: None of the variables has an upper bound
-
setUpperLimit
public void setUpperLimit(double[] bu)
Sets the upper limit of the constraints that have both a lower and an upper bound.- Parameters:
bu- adoublearray of length m containing the upper limit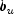 of the constraints that have both a
lower and an upper bound. If such a constraint exists, then method
of the constraints that have both a
lower and an upper bound. If such a constraint exists, then method
setConstraintTypemust be used to define the type of the constraints. IfconstraintType[i] != 3, i.e. if constraintiis not two-sided, then the corresponding entry inbu,bu[i], is ignored.Default: None of the constraints has an upper limit
-
solve
public void solve() throws SparseLP.DiagonalWeightMatrixException, SparseLP.CholeskyFactorizationAccuracyException, SparseLP.PrimalUnboundedException, SparseLP.PrimalInfeasibleException, SparseLP.DualInfeasibleException, SparseLP.InitialSolutionInfeasibleException, SparseLP.TooManyIterationsException, SparseLP.ProblemUnboundedException, SparseLP.ZeroColumnException, SparseLP.ZeroRowException, SparseLP.IncorrectlyEliminatedException, SparseLP.IncorrectlyActiveException, SparseLP.IllegalBoundsExceptionSolves the sparse linear programming problem by an infeasible primal-dual interior-point method.- Throws:
SparseLP.DiagonalWeightMatrixException- is thrown if a diagonal element of the diagonal weight matrix is too smallSparseLP.CholeskyFactorizationAccuracyException- is thrown if the Cholesky factorization failed because of accuracy problemsSparseLP.PrimalUnboundedException- is thrown if the primal problem is unboundedSparseLP.PrimalInfeasibleException- is thrown if the primal problem is infeasibleSparseLP.DualInfeasibleException- is thrown if the dual problem is infeasibleSparseLP.InitialSolutionInfeasibleException- is thrown if the initial solution for the one-row linear program is infeasibleSparseLP.TooManyIterationsException- is thrown if the maximum number of iterations has been exceededSparseLP.ProblemUnboundedException- is thrown if the problem is unboundedSparseLP.ZeroColumnException- is thrown if a column of the constraint matrix has no entriesSparseLP.ZeroRowException- is thrown if a row of the constraint matrix has no entriesSparseLP.IncorrectlyEliminatedException- is thrown if one or more LP variables are falsely characterized by the internal presolverSparseLP.IncorrectlyActiveException- is thrown if one or more LP variables are falsely characterized by the internal presolverSparseLP.IllegalBoundsException- is thrown if the lower bound is greater than the upper bound
-
-