- java.lang.Object
-
- com.imsl.math.Spline2D
-
- All Implemented Interfaces:
- Serializable, Cloneable
- Direct Known Subclasses:
- Spline2DInterpolate, Spline2DLeastSquares
public abstract class Spline2D extends Object implements Serializable, Cloneable
Represents and evaluates tensor-product splines.The simplest method of obtaining multivariate interpolation and approximation functions is to take univariate methods and form a multivariate method via tensor products. In the case of two-dimensional spline interpolation, the derivation proceeds as follows: Let
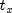 be a knot
sequence for splines of order
be a knot
sequence for splines of order 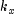 , and
, and
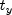 be a knot sequence for splines of order
be a knot sequence for splines of order
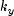 . Let
. Let 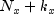 be the length
of
be the length
of 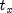 , and
, and 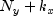 be the length
of
be the length
of 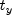 . Then, the tensor-product spline has the
following form:
. Then, the tensor-product spline has the
following form:
Given two sets of points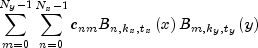
and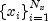
for which the corresponding univariate interpolation problem can be solved, the tensor-product interpolation problem finds the coefficients
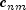 so that
so that
This problem can be solved efficiently by repeatedly solving univariate interpolation problems as described in de Boor (1978, p. 347).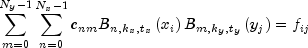
- See Also:
- Spline2DInterpolate Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description Spline2D()
-
Method Summary
Methods Modifier and Type Method and Description double[][]derivative(double[] xVec, double[] yVec, int xPartial, int yPartial)Returns the values of the partial derivative of the tensor-product spline of an array of points.doublederivative(double x, double y, int xPartial, int yPartial)Returns the value of the partial derivative of the tensor-product spline at the point (x, y).double[][]getCoefficients()Returns the coefficients for the tensor-product spline.double[]getXKnots()Returns the knot sequences in the x-direction.double[]getYKnots()Returns the knot sequences in the y-direction.doubleintegral(double a, double b, double c, double d)Returns the value of an integral of a tensor-product spline on a rectangular domain.double[][]value(double[] xVec, double[] yVec)Returns the values of the tensor-product spline of an array of points.doublevalue(double x, double y)Returns the value of the tensor-product spline at the point (x, y).
-
-
-
Method Detail
-
derivative
public double[][] derivative(double[] xVec, double[] yVec, int xPartial, int yPartial)Returns the values of the partial derivative of the tensor-product spline of an array of points.- Parameters:
xVec- adoublearray specifying the x-coordinates at which the spline is to be evaluated.yVec- adoublearray specifying the y-coordinates at which the spline is to be evaluated.xPartial- anintscalar specifying the x-partial derivative.yPartial- anintscalar specifying the y-partial derivative.- Returns:
- a
doublematrix containing the values of the partial derivatives
where i =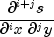
xPartialand j =yPartial, at each (x, y).
-
derivative
public double derivative(double x, double y, int xPartial, int yPartial)Returns the value of the partial derivative of the tensor-product spline at the point (x, y).- Parameters:
x- adoublescalar specifying the x-coordinate of the evaluation point for the tensor-product spline.y- adoublescalar specifying the y-coordinate of the evaluation point for the tensor-product spline.xPartial- anintscalar specifying the x-partial derivative.yPartial- anintscalar specifying the y-partial derivative.- Returns:
- a
doublescalar containing the value of the partial derivative
where i =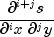
xPartialand j =yPartial, at (x, y).
-
getCoefficients
public double[][] getCoefficients()
Returns the coefficients for the tensor-product spline.- Returns:
- a
doublematrix containing the coefficients.
-
getXKnots
public double[] getXKnots()
Returns the knot sequences in the x-direction.- Returns:
- a
doublearray containing the knot sequences of the spline in the x-direction.
-
getYKnots
public double[] getYKnots()
Returns the knot sequences in the y-direction.- Returns:
- a
doublearray containing the knot sequences of the spline in the y-direction.
-
integral
public double integral(double a, double b, double c, double d)Returns the value of an integral of a tensor-product spline on a rectangular domain.If s is the spline, then the
integralmethod returns
This method uses the (univariate integration) identity (22) in de Boor (1978, p. 151)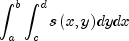
where![int_{t_0 }^x {sumlimits_{i = 0}^{n - 1} {alpha _i } } B_{i,k} left( tau right)dtau = sumlimits_{i = 0}^{r - 1} {left[ {sumlimits_{j = 0}^i {alpha _j frac{{t_{j + k} - t_j }}{k}} } right]} B_{i,k + 1} left( x right)](eqn_0734.png)
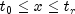 .
.
It assumes (for all knot sequences) that the first and last k knots are stacked, that is,
 and
and
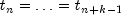 , where k is the order
of the spline in the x or y direction.
, where k is the order
of the spline in the x or y direction.- Parameters:
a- adoublespecifying the lower limit for the first variable of the tensor-product spline.b- adoublespecifying the upper limit for the first variable of the tensor-product spline.c- adoublespecifying the lower limit for the second variable of the tensor-product spline.d- adoublespecifying the upper limit for the second variable of the tensor-product spline.- Returns:
- a
double, the integral of the tensor-product spline over the rectangle[a, b]by[c, d].
-
value
public double[][] value(double[] xVec, double[] yVec)Returns the values of the tensor-product spline of an array of points.- Parameters:
xVec- adoublearray specifying the x-coordinates at which the spline is to be evaluated.yVec- adoublearray specifying the y-coordinates at which the spline is to be evaluated.- Returns:
- a
doublematrix containing the values evaluated.
-
value
public double value(double x, double y)Returns the value of the tensor-product spline at the point (x, y).- Parameters:
x- adoublescalar specifying the x-coordinate of the evaluation point for the tensor-product spline.y- adoublescalar specifying the y-coordinate of the evaluation point for the tensor-product spline.- Returns:
- a
doublescalar containing the value of the tensor-product spline.
-
-