- java.lang.Object
-
- com.imsl.stat.ANOVA
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class ANOVA extends Object implements Serializable, Cloneable
Analysis of Variance table and related statistics.- See Also:
- Example, Serialized Form
-
-
Field Summary
Fields Modifier and Type Field and Description static intBONFERRONIThe Bonferroni methodstatic intDUNN_SIDAKThe Dunn-Sidak methodstatic intONE_AT_A_TIMEThe One-at-a-Time (Fisher's LSD) methodstatic intSCHEFFEThe Scheffe methodstatic intTUKEYThe Tukey methodstatic intTUKEY_KRAMERThe Tukey-Kramer method
-
Constructor Summary
Constructors Constructor and Description ANOVA(double[][] y)/** Analyzes a one-way classification model.ANOVA(double dfr, double ssr, double dfe, double sse, double gmean)Construct an analysis of variance table and related statistics.
-
Method Summary
Methods Modifier and Type Method and Description doublegetAdjustedRSquared()Returns the adjusted R-squared (in percent).double[]getArray()Returns the ANOVA values as an array.doublegetCoefficientOfVariation()Returns the coefficient of variation (in percent).double[]getConfidenceInterval(double conLevel, int i, int j, int compMethod)Computes the confidence interval associated with the difference of means between two groups using a specified method.doublegetDegreesOfFreedomForError()Returns the degrees of freedom for error.doublegetDegreesOfFreedomForModel()Returns the degrees of freedom for model.doublegetErrorMeanSquare()Returns the error mean square.doublegetF()Returns the F statistic.double[][]getGroupInformation()Returns information concerning the groups.doublegetMeanOfY()Returns the mean of the response (dependent variable).doublegetModelErrorStdev()Returns the estimated standard deviation of the model error.doublegetModelMeanSquare()Returns the model mean square.doublegetP()Returns the p-value.doublegetRSquared()Returns the R-squared (in percent).doublegetSumOfSquaresForError()Returns the sum of squares for error.doublegetSumOfSquaresForModel()Returns the sum of squares for model.doublegetTotalDegreesOfFreedom()Returns the total degrees of freedom.intgetTotalMissing()Returns the total number of missing values.doublegetTotalSumOfSquares()Returns the total sum of squares.
-
-
-
Field Detail
-
BONFERRONI
public static final int BONFERRONI
The Bonferroni method- See Also:
- Constant Field Values
-
DUNN_SIDAK
public static final int DUNN_SIDAK
The Dunn-Sidak method- See Also:
- Constant Field Values
-
ONE_AT_A_TIME
public static final int ONE_AT_A_TIME
The One-at-a-Time (Fisher's LSD) method- See Also:
- Constant Field Values
-
SCHEFFE
public static final int SCHEFFE
The Scheffe method- See Also:
- Constant Field Values
-
TUKEY
public static final int TUKEY
The Tukey method- See Also:
- Constant Field Values
-
TUKEY_KRAMER
public static final int TUKEY_KRAMER
The Tukey-Kramer method- See Also:
- Constant Field Values
-
-
Constructor Detail
-
ANOVA
public ANOVA(double[][] y)
/** Analyzes a one-way classification model.- Parameters:
y- is a two-dimensiondoublearray containing the responses. The rows inycorrespond to observation groups. Each row ofycan contain a different number of observations.
-
ANOVA
public ANOVA(double dfr, double ssr, double dfe, double sse, double gmean)Construct an analysis of variance table and related statistics. Intended for use by the LinearRegression class.- Parameters:
dfr- adoublescalar value representing the degrees of freedom for model.ssr- adoublescalar value representing the sum of squares for model.dfe- adoublescalar value representing the degrees of freedom for error.sse- adoublescalar value representing the sum of squares for error.gmean- adoublescalar value representing the grand mean. If the grand mean is not known it may be set to not-a-number.
-
-
Method Detail
-
getAdjustedRSquared
public double getAdjustedRSquared()
Returns the adjusted R-squared (in percent).- Returns:
- a
doublescalar value representing the adjusted R-squared (in percent)
-
getArray
public double[] getArray()
Returns the ANOVA values as an array.- Returns:
- a
double[15] array containing the following values:index Value 0 Degrees of freedom for model 1 Degrees of freedom for error 2 Total degrees of freedom 3 Sum of squares for model 4 Sum of squares for error 5 Total sum of squares 6 Model mean square 7 Error mean square 8 F statistic 9 p-value 10 R-squared (in percent) 11 Adjusted R-squared (in percent) 12 Estimated standard deviation of the model error 13 Mean of the response (dependent variable) 14 Coefficient of variation (in percent)
-
getCoefficientOfVariation
public double getCoefficientOfVariation()
Returns the coefficient of variation (in percent).- Returns:
- a
doublescalar value representing the coefficient of variation (in percent)
-
getConfidenceInterval
public double[] getConfidenceInterval(double conLevel, int i, int j, int compMethod)Computes the confidence interval associated with the difference of means between two groups using a specified method.getConfidenceIntervalcomputes the simultaneous confidence interval on the pairwise comparison of means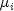 and
and 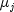 in the one-way analysis of
variance model. Any of several methods can be chosen. A good review of
these methods is given by Stoline (1981). Also the methods are discussed
in many elementary statistics texts, e.g., Kirk (1982, pages 114-127).
Let
in the one-way analysis of
variance model. Any of several methods can be chosen. A good review of
these methods is given by Stoline (1981). Also the methods are discussed
in many elementary statistics texts, e.g., Kirk (1982, pages 114-127).
Let 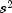 be the estimated variance of a single
observation. Let
be the estimated variance of a single
observation. Let  be the degrees of freedom
associated with
be the degrees of freedom
associated with 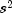 . Let
. Let
The methods are summarized as follows: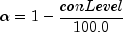
Tukey method: The Tukey method gives the narrowest simultaneous confidence intervals for the pairwise differences of means
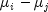 in balanced
in balanced  one-way designs. The method is exact and uses
the Studentized range distribution. The formula for the difference
one-way designs. The method is exact and uses
the Studentized range distribution. The formula for the difference
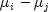 is given by
is given by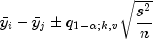
where
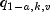 is the
is the 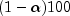 percentage point of the Studentized range distribution with
parameters
percentage point of the Studentized range distribution with
parameters  and
and  . If the
group sizes are unequal, the Tukey-Kramer method is used instead.
. If the
group sizes are unequal, the Tukey-Kramer method is used instead.Tukey-Kramer method: The Tukey-Kramer method is an approximate extension of the Tukey method for the unbalanced case. (The method simplifies to the Tukey method for the balanced case.) The method always produces confidence intervals narrower than the Dunn-Sidak and Bonferroni methods. Hayter (1984) proved that the method is conservative, i.e., the method guarantees a confidence coverage of at least
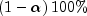 . Hayter's proof gave further support to
earlier recommendations for its use (Stoline 1981). (Methods that are
currently better are restricted to special cases and only offer
improvement in severely unbalanced cases, see, e.g., Spurrier and Isham
1985). The formula for the difference
. Hayter's proof gave further support to
earlier recommendations for its use (Stoline 1981). (Methods that are
currently better are restricted to special cases and only offer
improvement in severely unbalanced cases, see, e.g., Spurrier and Isham
1985). The formula for the difference 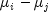 is given by the following:
is given by the following: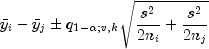
Dunn-Sidak method: The Dunn-Sidak method is a conservative method. The method gives wider intervals than the Tukey-Kramer method. (For large
 and small
and small  and k, the difference is only slight.) The method is slightly
better than the Bonferroni method and is based on an improved Bonferroni
(multiplicative) inequality (Miller, pages 101, 254-255). The method uses
the t distribution. The formula for the difference
and k, the difference is only slight.) The method is slightly
better than the Bonferroni method and is based on an improved Bonferroni
(multiplicative) inequality (Miller, pages 101, 254-255). The method uses
the t distribution. The formula for the difference 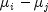 is given by
is given by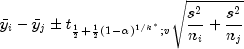
where
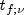 is the 100f percentage point
of the t distribution with
is the 100f percentage point
of the t distribution with  degrees of
freedom.
degrees of
freedom.Bonferroni method: The Bonferroni method is a conservative method based on the Bonferroni (additive) inequality (Miller, page 8). The method uses the t distribution. The formula for the difference
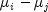 is given by
is given by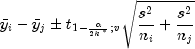
Scheffé method: The Scheffé method is an overly conservative method for simultaneous confidence intervals on pairwise difference of means. The method is applicable for simultaneous confidence intervals on all contrasts, i.e., all linear combinations
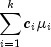
where the following is true:
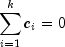
The method can be recommended here only if a large number of confidence intervals on contrasts in addition to the pairwise differences of means are to be constructed. The method uses the F distribution. The formula for the difference
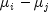 is given by
is given by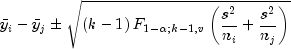
where
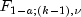 is the
is the
 percentage point of the
F distribution with
percentage point of the
F distribution with  and
and  degrees of freedom.
degrees of freedom.One-at-a-time t method (Fisher's LSD): The one-at-a-time t method is the method appropriate for constructing a single confidence interval. The confidence percentage input is appropriate for one interval at a time. The method has been used widely in conjunction with the overall test of the null hypothesis
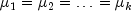 by the use of the F statistic. Fisher's LSD
(least significant difference) test is a two-stage test that proceeds to
make pairwise comparisons of means only if the overall F test is
significant. Milliken and Johnson (1984, page 31) recommend LSD
comparisons after a significant F only if the number of
comparisons is small and the comparisons were planned prior to the
analysis. If many unplanned comparisons are made, they recommend
Scheffe's method. If the F test is insignificant, a few planned
comparisons for differences in means can still be performed by using
either Tukey, Tukey-Kramer, Dunn-Sidak or Bonferroni methods. Because the
F test is insignificant, Scheffe's method will not yield any
significant differences. The formula for the difference
by the use of the F statistic. Fisher's LSD
(least significant difference) test is a two-stage test that proceeds to
make pairwise comparisons of means only if the overall F test is
significant. Milliken and Johnson (1984, page 31) recommend LSD
comparisons after a significant F only if the number of
comparisons is small and the comparisons were planned prior to the
analysis. If many unplanned comparisons are made, they recommend
Scheffe's method. If the F test is insignificant, a few planned
comparisons for differences in means can still be performed by using
either Tukey, Tukey-Kramer, Dunn-Sidak or Bonferroni methods. Because the
F test is insignificant, Scheffe's method will not yield any
significant differences. The formula for the difference 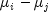 is given by
is given by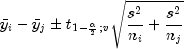
- Parameters:
conLevel- adoublespecifying the confidence level for simultaneous interval estimation. If the Tukey method for computing the confidence intervals on the pairwise difference of means is to be used,conLevelmust be in the range [90.0, 99.0]. Otherwise,conLevelmust be in the range
[0.0, 100.0). One normally sets this value to 95.0.i- is anintindicating the i-th member of the pair difference,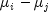 .
. imust be a valid group index.j- is anintindicating the j-th member of the pair difference,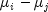 .
. jmust be a valid group index.compMethod- must be one of the following:compMethod Description TUKEY Uses the Tukey method. This method is valid for balanced one-way designs. TUKEY_KRAMER Uses the Tukey-Kramer method. This method simplifies to the Tukey method for the balanced case. DUNN_SIDAK Uses the Dunn-Sidak method. BONFERRONI Uses the Bonferroni method. SCHEFFE Uses the Scheffe method. ONE_AT_A_TIME Uses the One-at-a-Time (Fisher's LSD) method. - Returns:
- a
doublearray containing the group numbers, difference of means, and lower and upper confidence limits.Array Element Description 0 Group number for the i-th mean. 1 Group number for the j-th mean. 2 Difference of means (i-th mean) - (j-th mean). 3 Lower confidence limit for the difference. 4 Upper confidence limit for the difference.
-
getDegreesOfFreedomForError
public double getDegreesOfFreedomForError()
Returns the degrees of freedom for error.- Returns:
- a
doublescalar value representing the degrees of freedom for error
-
getDegreesOfFreedomForModel
public double getDegreesOfFreedomForModel()
Returns the degrees of freedom for model.- Returns:
- a
doublescalar value representing the degrees of freedom for model
-
getErrorMeanSquare
public double getErrorMeanSquare()
Returns the error mean square.- Returns:
- a
doublescalar value representing the error mean square
-
getF
public double getF()
Returns the F statistic.- Returns:
- a
doublescalar value representing the F statistic
-
getGroupInformation
public double[][] getGroupInformation()
Returns information concerning the groups.- Returns:
- a two-dimension
doublearray containing information concerning the groups. Row i contains information pertaining to the i-th group. The information in the columns is as follows:Column Information 0 Group Number 1 Number of nonmissing observations 2 Group Mean 3 Group Standard Deviation
-
getMeanOfY
public double getMeanOfY()
Returns the mean of the response (dependent variable).- Returns:
- a
doublescalar value representing the mean of the response (dependent variable)
-
getModelErrorStdev
public double getModelErrorStdev()
Returns the estimated standard deviation of the model error.- Returns:
- a
doublescalar value representing the estimated standard deviation of the model error
-
getModelMeanSquare
public double getModelMeanSquare()
Returns the model mean square.- Returns:
- a
doublescalar value representing the model mean square
-
getP
public double getP()
Returns the p-value.- Returns:
- a
doublescalar value representing the p-value
-
getRSquared
public double getRSquared()
Returns the R-squared (in percent).- Returns:
- a
doublescalar value representing the R-squared (in percent)
-
getSumOfSquaresForError
public double getSumOfSquaresForError()
Returns the sum of squares for error.- Returns:
- a
doublescalar value representing the sum of squares for error
-
getSumOfSquaresForModel
public double getSumOfSquaresForModel()
Returns the sum of squares for model.- Returns:
- a
doublescalar value representing the sum of squares for model
-
getTotalDegreesOfFreedom
public double getTotalDegreesOfFreedom()
Returns the total degrees of freedom.- Returns:
- a
doublescalar value representing the total degrees of freedom
-
getTotalMissing
public int getTotalMissing()
Returns the total number of missing values.- Returns:
- an
intscalar value representing the total number of missing values (NaN) in input Y. Elements of Y containing NaN (not a number) are omitted from the computations.
-
getTotalSumOfSquares
public double getTotalSumOfSquares()
Returns the total sum of squares.- Returns:
- a
doublescalar value representing the total sum of squares
-
-