- java.lang.Object
-
- com.imsl.stat.AutoCorrelation
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class AutoCorrelation extends Object implements Serializable, Cloneable
Computes the sample autocorrelation function of a stationary time series.AutoCorrelationestimates the autocorrelation function of a stationary time series given a sample of n observations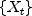 for
for
 .
.Let
be the estimate of the mean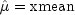
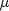 of the time series
of the time series 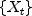 where
where
The autocovariance function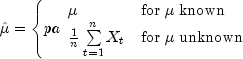
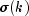 is estimated
by
is estimated
by
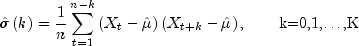
where K =
maximum_lag. Note that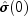 is an estimate of the sample variance. The
autocorrelation function
is an estimate of the sample variance. The
autocorrelation function 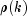 is estimated by
is estimated by

Note that
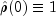 by definition.
by definition.
The standard errors of sample autocorrelations may be optionally computed according to the getStandardErrors method argument
stderrMethod. One method (Bartlett 1946) is based on a general asymptotic expression for the variance of the sample autocorrelation coefficient of a stationary time series with independent, identically distributed normal errors. The theoretical formula is![mbox{var}{hat rho(k)} =
frac{1}{n}sumlimits_{i=-infty}^{infty}
left[{rho^2(i)}+rho(i-k)rho(i+k)-4rho(i)
rho(k)rho(i-k)+2rho^2(i)rho^2(k)right]](eqn_3815.png)
where
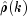 assumes
assumes
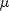 is unknown. For computational purposes, the
autocorrelations
is unknown. For computational purposes, the
autocorrelations 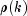 are replaced by their
estimates
are replaced by their
estimates  for
for
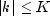 , and the limits of summation
are bounded because of the assumption that
, and the limits of summation
are bounded because of the assumption that
 for all
for all 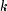 such
that
such
that 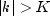 .
.A second method (Moran 1947) utilizes an exact formula for the variance of the sample autocorrelation coefficient of a random process with independent, identically distributed normal errors. The theoretical formula is
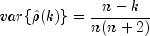
where
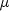 is assumed to be equal to zero. Note
that this formula does not depend on the autocorrelation function.
is assumed to be equal to zero. Note
that this formula does not depend on the autocorrelation function.
The method
getPartialAutoCorrelationsestimates the partial autocorrelations of the stationary time series given K =maximum_lagsample autocorrelations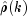 for k=0,1,...,K. Consider the AR(k)
process defined by
for k=0,1,...,K. Consider the AR(k)
process defined by
where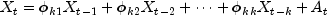
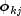 denotes the j-th
coefficient in the process. The set of estimates
denotes the j-th
coefficient in the process. The set of estimates 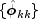 for k = 1, ..., K is the sample partial
autocorrelation function. The autoregressive parameters
for k = 1, ..., K is the sample partial
autocorrelation function. The autoregressive parameters
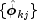 for j = 1, ..., k
are approximated by Yule-Walker estimates for successive AR(k)
models where k = 1, ..., K. Based on the sample Yule-Walker
equations
for j = 1, ..., k
are approximated by Yule-Walker estimates for successive AR(k)
models where k = 1, ..., K. Based on the sample Yule-Walker
equations
a recursive relationship for k=1, ..., K was developed by Durbin (1960). The equations are given by
and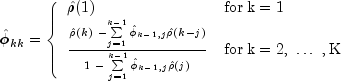
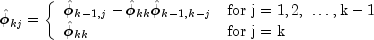
This procedure is sensitive to rounding error and should not be used if the parameters are near the nonstationarity boundary. A possible alternative would be to estimate
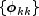 for successive AR(k) models using least or maximum likelihood.
Based on the hypothesis that the true process is AR(p), Box and
Jenkins (1976, page 65) note
for successive AR(k) models using least or maximum likelihood.
Based on the hypothesis that the true process is AR(p), Box and
Jenkins (1976, page 65) note 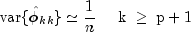
See Box and Jenkins (1976, pages 82-84) for more information concerning the partial autocorrelation function.
- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classAutoCorrelation.NonPosVariancesExceptionThe problem is ill-conditioned.
-
Field Summary
Fields Modifier and Type Field and Description static intBARTLETTS_FORMULAIndicates standard error computation using Bartlett's formula.static intMORANS_FORMULAIndicates standard error computation using Moran's formula.
-
Constructor Summary
Constructors Constructor and Description AutoCorrelation(double[] x, int maximum_lag)Constructor to compute the sample autocorrelation function of a stationary time series.
-
Method Summary
Methods Modifier and Type Method and Description double[]getAutoCorrelations()Returns the autocorrelations of the time seriesx.double[]getAutoCovariances()Returns the variance and autocovariances of the time seriesx.doublegetMean()Returns the mean of the time seriesx.intgetNumberOfThreads()Returns the number ofjava.lang.Threadinstances used for parallel processing.double[]getPartialAutoCorrelations()Returns the sample partial autocorrelation function of the stationary time seriesx.double[]getStandardErrors(int stderrMethod)Returns the standard errors of the autocorrelations of the time seriesx.doublegetVariance()Returns the variance of the time seriesx.voidsetMean(double mean)Estimate mean of the time seriesx.voidsetNumberOfThreads(int numberOfThreads)Sets the number ofjava.lang.Threadinstances to be used for parallel processing.
-
-
-
Field Detail
-
BARTLETTS_FORMULA
public static final int BARTLETTS_FORMULA
Indicates standard error computation using Bartlett's formula.- See Also:
- Constant Field Values
-
MORANS_FORMULA
public static final int MORANS_FORMULA
Indicates standard error computation using Moran's formula.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
AutoCorrelation
public AutoCorrelation(double[] x, int maximum_lag)Constructor to compute the sample autocorrelation function of a stationary time series.- Parameters:
x- a one-dimensionaldoublearray containing the stationary time seriesmaximum_lag- anintcontaining the maximum lag of autocovariance, autocorrelations, and standard errors of autocorrelations to be computed.maximum_lagmust be greater than or equal to 1 and less than the number of observations inx
-
-
Method Detail
-
getAutoCorrelations
public double[] getAutoCorrelations()
Returns the autocorrelations of the time seriesx.- Returns:
- a
doublearray of lengthmaximum_lag+1 containing the autocorrelations of the time seriesx. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag where k = 1, ...,
where k = 1, ...,
maximum_lag.
-
getAutoCovariances
public double[] getAutoCovariances() throws AutoCorrelation.NonPosVariancesExceptionReturns the variance and autocovariances of the time seriesx.- Returns:
- a
doublearray of lengthmaximum_lag+1 containing the variances and autocovariances of the time seriesx. The 0-th element of the array contains the variance of the time seriesx. The k-th element contains the autocovariance of lag k where k = 1, ...,maximum_lag. - Throws:
AutoCorrelation.NonPosVariancesException- is thrown if the problem is ill-conditioned
-
getMean
public double getMean()
Returns the mean of the time seriesx.- Returns:
- a
doublecontaining the mean
-
getNumberOfThreads
public int getNumberOfThreads()
Returns the number ofjava.lang.Threadinstances used for parallel processing.- Returns:
- an
intcontaining the number ofjava.lang.Threadinstances used for parallel processing.
-
getPartialAutoCorrelations
public double[] getPartialAutoCorrelations()
Returns the sample partial autocorrelation function of the stationary time seriesx.- Returns:
- a
doublearray of lengthmaximum_lagcontaining the partial autocorrelations of the time seriesx.
-
getStandardErrors
public double[] getStandardErrors(int stderrMethod)
Returns the standard errors of the autocorrelations of the time seriesx. Method of computation for standard errors of the autocorrelation is chosen by thestderrMethodparameter. IfstderrMethodis set toBARTLETTS_FORMULA, Bartlett's formula is used to compute the standard errors of autocorrelations. IfstderrMethodis set toMORANS_FORMULA, Moran's formula is used to compute the standard errors of autocorrelations.- Parameters:
stderrMethod- anintspecifying the method to compute the standard errors of autocorrelations of the time seriesx- Returns:
- a
doublearray of lengthmaximum_lagcontaining the standard errors of the autocorrelations of the time seriesx
-
getVariance
public double getVariance()
Returns the variance of the time seriesx.- Returns:
- a
doublecontaining the variance of the time seriesx
-
setMean
public void setMean(double mean)
Estimate mean of the time seriesx.- Parameters:
mean- adoublecontaining the estimate mean of the time seriesx.
-
setNumberOfThreads
public void setNumberOfThreads(int numberOfThreads)
Sets the number ofjava.lang.Threadinstances to be used for parallel processing.- Parameters:
numberOfThreads- anintspecifying the number ofjava.lang.Threadinstances to be used for parallel processing.Default:
numberOfThreads= 1.
-
-