- java.lang.Object
-
- com.imsl.stat.CategoricalGenLinModel
-
public class CategoricalGenLinModel extends Object
Analyzes categorical data using logistic, probit, Poisson, and other linear models.Reweighted least squares is used to compute (extended) maximum likelihood estimates in some generalized linear models involving categorized data. One of several models, including probit, logistic, Poisson, logarithmic, and negative binomial models, may be fit for input point or interval observations. (In the usual case, only point observations are observed.)
Let
be the linear response where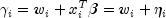
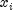 is a design column
vector obtained from a row of
is a design column
vector obtained from a row of 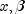 is the column
vector of coefficients to be estimated, and
is the column
vector of coefficients to be estimated, and 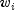 is a
fixed parameter that may be input in
is a
fixed parameter that may be input in x. When some of the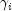 are infinite at the supremum of the
likelihood, then extended maximum likelihood estimates are computed.
Extended maximum likelihood are computed as the finite (but nonunique)
estimates
are infinite at the supremum of the
likelihood, then extended maximum likelihood estimates are computed.
Extended maximum likelihood are computed as the finite (but nonunique)
estimates 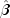 that optimize the likelihood
containing only the observations with finite
that optimize the likelihood
containing only the observations with finite 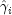 . These estimates, when combined with the set of indices of the
observations such that
. These estimates, when combined with the set of indices of the
observations such that 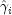 is infinite at
the supremum of the likelihood, are called extended maximum estimates. When
none of the optimal
is infinite at
the supremum of the likelihood, are called extended maximum estimates. When
none of the optimal 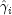 are infinite,
extended maximum likelihood estimates are identical to maximum likelihood
estimates. Extended maximum likelihood estimation is discussed in more
detail by Clarkson and Jennrich (1991). In
are infinite,
extended maximum likelihood estimates are identical to maximum likelihood
estimates. Extended maximum likelihood estimation is discussed in more
detail by Clarkson and Jennrich (1991). In
CategoricalGenLinModel, observations with potentially infinite
are detected and removed from the likelihood if
infin= 0. See below.The models available in CategoricalGenLinModel are:
Model Name Parameterization Response PDF MODEL0 (Poisson) 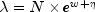
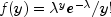
MODEL1 (Negative Binomial) 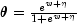
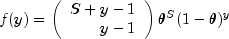
MODEL2 (Logarithmic) 
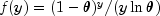
MODEL3 (Logistic) 

MODEL4 (Probit) 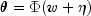
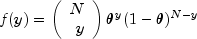
MODEL5 (Log-log) 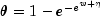
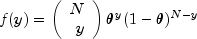
Here
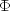 denotes the cumulative normal
distribution, N and S are known parameters specified for each
observation via column
denotes the cumulative normal
distribution, N and S are known parameters specified for each
observation via column iparofx, and w is an optional fixed parameter specified for each observation via columnifixofx. (By default N is taken to be 1 formodel= 0, 3, 4 and 5 and S is taken to be 1 formodel= 1. By default w is taken to be 0.) Since the log-log model (model= 5) probabilities are not symmetric with respect to 0.5, quantitatively, as well as qualitatively, different models result when the definitions of "success" and "failure" are interchanged in this distribution. In this model and all other models involving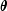 ,
, 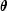 is
taken to be the probability of a "success."
is
taken to be the probability of a "success."Note that each row vector in the data matrix can represent a single observation; or, through the use of column
ifrqof the matrixx, each vector can represent several observations.Computational Details
For interval observations, the probability of the observation is computed by summing the probability distribution function over the range of values in the observation interval. For right-interval observations,
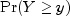 is computed as a sum based upon the equality
is computed as a sum based upon the equality 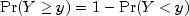 . Derivatives are computed similarly.
. Derivatives are computed similarly.
CategoricalGenLinModelallows three types of interval observations. In full interval observations, both the lower and the upper endpoints of the interval must be specified. For right-interval observations, only the lower endpoint need be given while for left-interval observations, only the upper endpoint is given.The computations proceed as follows:
- The input parameters are checked for consistency and validity.
- Estimates of the means of the "independent" or design variables are
computed. The frequency of the observation in all but binomial
distribution model is taken from column
ifrqof the data matrixx. In binomial distribution models, the frequency is taken as the product of n =x[i][ipar]andx[i][ifrq]. In all cases these values default to 1. Means are computed as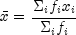
- If
init= 0, initial estimates of the coefficients are obtained (based upon the observation intervals) as multiple regression estimates relating transformed observation probabilities to the observation design vector. For example, in the binomial distribution models,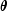 for point
observations may be estimated as
for point
observations may be estimated as
and, when![hat{theta}=x[i][irt]/x[i][ipar]](eqn_3746.png)
model= 3, the linear relationship is given by
while if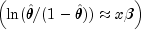
model= 4,
For bounded interval observations, the midpoint of the interval is used for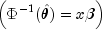
x[i][irt]. Right-interval observations are not used in obtaining initial estimates when the distribution has unbounded support (since the midpoint of the interval is not defined). When computing initial estimates, standard modifications are made to prevent illegal operations such as division by zero.Regression estimates are obtained at this point, as well as later, by use of linear regression.
- Newton-Raphson iteration for the maximum likelihood estimates is
implemented via iteratively reweighted least squares. Let
denote the log of the probability of the i-th observation for coefficients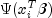
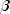 . In the least-squares model,
the weight of the i-th observation is taken as the absolute
value of the second derivative of
. In the least-squares model,
the weight of the i-th observation is taken as the absolute
value of the second derivative of
with respect to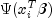
(times the frequency of the observation), and the dependent variable is taken as the first derivative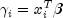
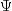 with
respect to
with
respect to 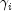 , divided by the square root
of the weight times the frequency. The Newton step is given by
, divided by the square root
of the weight times the frequency. The Newton step is given by
where all derivatives are evaluated at the current estimate of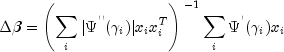
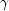 , and
, and  . This step is computed as the estimated
regression coefficients in the least-squares model. Step halving is
used when necessary to ensure a decrease in the criterion.
. This step is computed as the estimated
regression coefficients in the least-squares model. Step halving is
used when necessary to ensure a decrease in the criterion. - Convergence is assumed when the maximum relative change in any
coefficient update from one iteration to the next is less than
epsor when the relative change in the log-likelihood from one iteration to the next is less thaneps/100. Convergence is also assumed aftermaxIterationsor when step halving leads to a step size of less than .0001 with no increase in the log-likelihood. - For interval observations, the contribution to the log-likelihood is the log of the sum of the probabilities of each possible outcome in the interval. Because the distributions are discrete, the sum may involve many terms. The user should be aware that data with wide intervals can lead to expensive (in terms of computer time) computations.
- If
setInfiniteEstimateMethodset to 0, then the methods of Clarkson and Jennrich (1991) are used to check for the existence of infinite estimates in
As an example of a situation in which infinite estimates can occur, suppose that observation j is right censored with
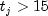 in a logistic model. If design matrix
in a logistic model. If design matrix xis is such that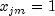 and
and  for all
for all  , then the
optimal estimate of
, then the
optimal estimate of 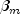 occurs at
occurs at
leading to an infinite estimate of both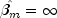
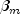 and
and 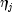 . In
. In CategoricalGenLinModel, such estimates may be "computed."In all models fit by
CategoricalGenLinModel, infinite estimates can only occur when the optimal estimated probability associated with the left- or right-censored observation is 1. IfsetInfiniteEstimateMethodset to 0, left- or right- censored observations that have estimated probability greater than 0.995 at some point during the iterations are excluded from the log-likelihood, and the iterations proceed with a log-likelihood based upon the remaining observations. This allows convergence of the algorithm when the maximum relative change in the estimated coefficients is small and also allows for the determination of observations with infinite
At convergence, linear programming is used to ensure that the eliminated observations have infinite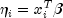
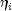 .
If some (or all) of the removed observations should not have been
removed (because their estimated
.
If some (or all) of the removed observations should not have been
removed (because their estimated 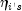 must be finite), then the iterations are restarted with a
log-likelihood based upon the finite
must be finite), then the iterations are restarted with a
log-likelihood based upon the finite 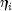 observations. See Clarkson and Jennrich (1991) for more details.
observations. See Clarkson and Jennrich (1991) for more details.
When
setInfiniteEstimateMethodis set to 1, no observations are eliminated during the iterations. In this case, when infinite estimates occur, some (or all) of the coefficient estimates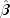 will become large, and it is likely
that the Hessian will become (numerically) singular prior to convergence.
will become large, and it is likely
that the Hessian will become (numerically) singular prior to convergence.When infinite estimates for the
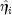 are detected, linear regression (see Chapter 2, Regression;)
is used at the convergence of the algorithm to obtain unique
estimates
are detected, linear regression (see Chapter 2, Regression;)
is used at the convergence of the algorithm to obtain unique
estimates 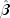 . This is accomplished by
regressing the optimal
. This is accomplished by
regressing the optimal 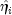 or the
observations with finite
or the
observations with finite 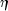 against
against
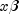 , yielding a unique
, yielding a unique  (by setting coefficients
(by setting coefficients 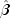 that are linearly related to previous coefficients in
the model to zero). All of the final statistics relating to
that are linearly related to previous coefficients in
the model to zero). All of the final statistics relating to
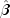 are based upon these estimates.
are based upon these estimates. - Residuals are computed according to methods discussed by Pregibon
(1981). Let
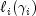 denote the
log-likelihood of the i-th observation evaluated at
denote the
log-likelihood of the i-th observation evaluated at
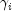 . Then, the standardized residual is
computed as
. Then, the standardized residual is
computed as
where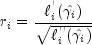
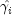 is the value of
is the value of 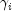 when evaluated at the optimal
when evaluated at the optimal 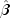 and the derivatives here (and only here) are with
respect to
and the derivatives here (and only here) are with
respect to 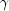 rather than with respect to
rather than with respect to
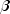 . The denominator of this expression is
used as the "standard error of the residual" while the numerator is
the "raw" residual.
. The denominator of this expression is
used as the "standard error of the residual" while the numerator is
the "raw" residual.
Following Cook and Weisberg (1982), we take the influence of the i-th observation to be
This quantity is a one-step approximation to the change in the estimates when the i-th observation is deleted. Here, the partial derivatives are with respect to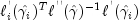
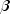 .
.
Programming Notes
- Classification variables are specified via
setClassificationVariableColumn. Indicator or dummy variables are created for the classification variables. - To enhance precision "centering" of covariates is performed if
setModelInterceptis set to 1 and (number of observations) - (number of rows inxmissing one or more values)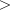 1. In doing so, the
sample means of the design variables are subtracted from each
observation prior to its inclusion in the model. On convergence the
intercept, its variance and its covariance with the remaining
estimates are transformed to the uncentered estimate values.
1. In doing so, the
sample means of the design variables are subtracted from each
observation prior to its inclusion in the model. On convergence the
intercept, its variance and its covariance with the remaining
estimates are transformed to the uncentered estimate values. - Two methods for specifying a binomial distribution model are
possible. In the first method,
x[i][ifrq]contains the frequency of the observation whilex[i][irt]is 0 or 1 depending upon whether the observation is a success or failure. In this case, N =x[i][ipar]is always 1. The model is treated as repeated Bernoulli trials, and interval observations are not possible.
A second method for specifying binomial models is to use
x[i][irt]to represent the number of successes in thex[i][ipar]trials. In this case,x[i][ifrq]will usually be 1, but it may be greater than 1, in which case interval observations are possible.Note that the
solvemethod must be called prior to calling the "get" member functions, otherwise anullis returned.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classCategoricalGenLinModel.ClassificationVariableExceptionThe ClassificationVariable vector has not been initialized.static classCategoricalGenLinModel.ClassificationVariableLimitExceptionThe Classification Variable limit set by the user throughsetUpperBoundhas been exceeded.static classCategoricalGenLinModel.ClassificationVariableValueExceptionThe number of distinct values for each Classification Variable must be greater than 1.static classCategoricalGenLinModel.DeleteObservationsExceptionThe number of observations to be deleted (set bysetObservationMax) has grown too large.static classCategoricalGenLinModel.RankDeficientExceptionThe model has been determined to be rank deficient.
-
Field Summary
Fields Modifier and Type Field and Description static intMODEL0Indicates an exponential function is used to model the distribution parameter.static intMODEL1Indicates a logistic function is used to model the distribution parameter.static intMODEL2Indicates a logistic function is used to model the distribution parameter.static intMODEL3Indicates a logistic function is used to model the distribution parameter.static intMODEL4Indicates a probit function is used to model the distribution parameter.static intMODEL5Indicates a log-log function is used to model the distribution parameter.
-
Constructor Summary
Constructors Constructor and Description CategoricalGenLinModel(double[][] x, int model)Constructs a newCategoricalGenLinModel.
-
Method Summary
Methods Modifier and Type Method and Description double[][]getCaseAnalysis()Returns the case analysis.int[]getClassificationVariableCounts()Returns the number of values taken by each classification variable.double[]getClassificationVariableValues()Returns the distinct values of the classification variables in ascending order.double[][]getCovarianceMatrix()Returns the estimated asymptotic covariance matrix of the coefficients.double[]getDesignVariableMeans()Returns the means of the design variables.int[]getExtendedLikelihoodObservations()Returns a vector indicating which observations are included in the extended likelihood.double[][]getHessian()Returns the Hessian computed at the initial parameter estimates.double[]getLastParameterUpdates()Returns the last parameter updates (excluding step halvings).intgetNRowsMissing()Returns the number of rows of data inxthat contain missing values in one or more specific columns ofx.doublegetOptimizedCriterion()Returns the optimized criterion.double[][]getParameters()Returns the parameter estimates and associated statistics.double[]getProduct()Returns the inverse of the Hessian times the gradient vector computed at the input parameter estimates.voidsetCensorColumn(int icen)Sets the column number inxwhich contains the interval type for each observation.voidsetClassificationVariableColumn(int[] indcl)Initializes an index vector to contain the column numbers inxthat are classification variables.voidsetConvergenceTolerance(double eps)Set the convergence criterion.voidsetEffects(int[] indef, int[] nvef)Initializes an index vector to contain the column numbers inxassociated with each effect.voidsetExtendedLikelihoodObservations(int[] iadds)Initializes a vector indicating which observations are to be included in the extended likelihood.voidsetFixedParameterColumn(int ifix)Sets the column number inxthat contains a fixed parameter for each observation that is added to the linear response prior to computing the model parameter.voidsetFrequencyColumn(int ifrq)Sets the column number inxthat contains the frequency of response for each observation.voidsetInfiniteEstimateMethod(int infin)Sets the method to be used for handling infinite estimates.voidsetInitialEstimates(int init, double[] estimates)Sets the initial parameter estimates option.voidsetLowerEndpointColumn(int irt)Sets the column number inxthat contains the lower endpoint of the observation interval for full interval and right interval observations.voidsetMaxIterations(int maxIterations)Set the maximum number of iterations allowed.voidsetModelIntercept(int intcep)Sets the intercept option.voidsetObservationMax(int nmax)Sets the maximum number of observations that can be handled in the linear programming.voidsetOptionalDistributionParameterColumn(int ipar)Sets the column number inxthat contains an optional distribution parameter for each observation.voidsetTolerance(double tol)Initializes the tolerance used in determining linear dependence.voidsetUpperBound(int maxcl)Sets the upper bound on the sum of the number of distinct values taken on by each classification variable.voidsetUpperEndpointColumn(int ilt)Sets the column number inxthat contains the upper endpoint of the observation interval for full interval and left interval observations.double[][]solve()Returns the parameter estimates and associated statistics for a CategoricalGenLinModel object.
-
-
-
Field Detail
-
MODEL0
public static final int MODEL0
Indicates an exponential function is used to model the distribution parameter. The distribution of the response variable is Poisson. The lower bound of the response variable is 0.- See Also:
- Constant Field Values
-
MODEL1
public static final int MODEL1
Indicates a logistic function is used to model the distribution parameter. The distribution of the response variable is negative Binomial. The lower bound of the response variable is 0.- See Also:
- Constant Field Values
-
MODEL2
public static final int MODEL2
Indicates a logistic function is used to model the distribution parameter. The distribution of the response variable is Logarithmic. The lower bound of the response variable is 1.- See Also:
- Constant Field Values
-
MODEL3
public static final int MODEL3
Indicates a logistic function is used to model the distribution parameter. The distribution of the response variable is Binomial. The lower bound of the response variable is 0.- See Also:
- Constant Field Values
-
MODEL4
public static final int MODEL4
Indicates a probit function is used to model the distribution parameter. The distribution of the response variable is Binomial. The lower bound of the response variable is 0.- See Also:
- Constant Field Values
-
MODEL5
public static final int MODEL5
Indicates a log-log function is used to model the distribution parameter. The distribution of the response variable is Binomial. The lower bound of the response variable is 0.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
CategoricalGenLinModel
public CategoricalGenLinModel(double[][] x, int model)Constructs a newCategoricalGenLinModel.- Parameters:
x- Adoubleinput matrix containing the data where the number of rows in the matrix is equal to the number of observations.model- Anintscalar which specifies the distribution of the response variable and the function used to model the distribution parameter. Use one of the class members from the following table. The lower bound given in the table is the minimum possible value of the response variable:
LetModel Distribution Function Lower-bound 0 Poisson Exponential 0 1 Negative Binomial Logistic 0 2 Logarithmic Logistic 1 3 Binomial Logistic 0 4 Binomial Probit 0 5 Binomial Log-log 0 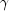 be the dot product of a
row in the design matrix with the parameters (plus the
fixed parameter, if used). Then, the functions used to
model the distribution parameter are given by:
be the dot product of a
row in the design matrix with the parameters (plus the
fixed parameter, if used). Then, the functions used to
model the distribution parameter are given by:
Name Function Exponential 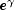
Logistic 
Probit 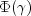 (where
(where
 is the normal cdf)
is the normal cdf)
Log-log 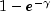
-
-
Method Detail
-
getCaseAnalysis
public double[][] getCaseAnalysis()
Returns the case analysis.- Returns:
- A
doublematrix containing the case analysis ornullifsolvehas not been called. The matrix is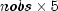 where nobs
is the number of observations. The matrix contains:
where nobs
is the number of observations. The matrix contains:
Case studies are computed for all observations except where missing values prevent their computation. The prediction in column 0 depends upon the model used as follows:Column Statistic 0 Prediction. 1 The residual. 2 The estimated standard error of the residual. 3 The estimated influence of the observation. 4 The standardized residual. Model Prediction 0 The predicted mean for the observation. 1-4 The probability of a success on a single trial.
-
getClassificationVariableCounts
public int[] getClassificationVariableCounts() throws CategoricalGenLinModel.ClassificationVariableExceptionReturns the number of values taken by each classification variable.- Returns:
- An
intarray of length nclvar containing the number of values taken by each classification variable where nclvar is the number of classification variables ornullifsolvehas not been called. - Throws:
CategoricalGenLinModel.ClassificationVariableException- is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1
-
getClassificationVariableValues
public double[] getClassificationVariableValues() throws CategoricalGenLinModel.ClassificationVariableExceptionReturns the distinct values of the classification variables in ascending order.- Returns:
- A
doublearray of length![sum_{k=0}^{
mbox{nclvar}}mbox{nclval[k]}](eqn_3798.png) containing the
distinct values of the classification variables in ascending
order where nclvar is the number of classification
variables and nclval[i] is the number of values taken by
the i-th classification variable. A
containing the
distinct values of the classification variables in ascending
order where nclvar is the number of classification
variables and nclval[i] is the number of values taken by
the i-th classification variable. A nullis returned ifsolvehas not been called prior to calling this method. - Throws:
CategoricalGenLinModel.ClassificationVariableException- is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1
-
getCovarianceMatrix
public double[][] getCovarianceMatrix()
Returns the estimated asymptotic covariance matrix of the coefficients.- Returns:
- A
doublematrix containing the estimated asymptotic covariance matrix of the coefficients ornullifsolvehas not been called. The covariance matrix is nCoef by nCoef where nCoef is the number of coefficients in the model.
-
getDesignVariableMeans
public double[] getDesignVariableMeans()
Returns the means of the design variables.- Returns:
- A
doublearray of length nCoef containing the means of the design variables where nCoef is the number of coefficients in the model ornullifsolvehas not been called.
-
getExtendedLikelihoodObservations
public int[] getExtendedLikelihoodObservations()
Returns a vector indicating which observations are included in the extended likelihood.- Returns:
- An
intarray of length nobs indicating which observations are included in the extended likelihood where nobs is the number of observations. The values within the array are interpreted as:
AValue Status of observation 0 Observation i is in the likelihood. 1 Observation i cannot be in the likelihood because it contains at least one missing value in x.2 Observation i is not in the likelihood. Its estimated parameter is infinite. nullis returned ifsolvehas not been called prior to calling this method.
-
getHessian
public double[][] getHessian() throws CategoricalGenLinModel.ClassificationVariableException, CategoricalGenLinModel.ClassificationVariableLimitException, CategoricalGenLinModel.ClassificationVariableValueException, CategoricalGenLinModel.DeleteObservationsException, CategoricalGenLinModel.RankDeficientException, SVD.DidNotConvergeExceptionReturns the Hessian computed at the initial parameter estimates.- Returns:
- A
doublematrix containing the Hessian computed at the input parameter estimates. The Hessian matrix is nCoef by nCoef where nCoef is the number of coefficients in the model. This member function will callsolveto get the Hessian if the Hessian has not already been computed. - Throws:
CategoricalGenLinModel.ClassificationVariableException- is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1CategoricalGenLinModel.ClassificationVariableLimitException- is thrown when the sum of the number of distinct values taken on by each classification variable exceeds the maximum allowed,maxclCategoricalGenLinModel.DeleteObservationsException- is thrown if the number of observations to be deleted has grown too largeCategoricalGenLinModel.ClassificationVariableValueExceptionCategoricalGenLinModel.RankDeficientExceptionSVD.DidNotConvergeException
-
getLastParameterUpdates
public double[] getLastParameterUpdates()
Returns the last parameter updates (excluding step halvings).- Returns:
- A
doublearray of length nCoef containing the last parameter updates (excluding step halvings) ornullifsolvehas not been called.
-
getNRowsMissing
public int getNRowsMissing()
Returns the number of rows of data inxthat contain missing values in one or more specific columns ofx.- Returns:
- An
intscalar representing the number of rows of data inxthat contain missing values in one or more specific columns ofxornullifsolvehas not been called. The columns ofxincluded in the count are the columns containing the upper or lower endpoints of full interval, left interval, or right interval observations. Also included are the columns containing the frequency responses, fixed parameters, optional distribution parameters, and interval type for each observation. Columns containing classification variables and columns associated with each effect in the model are also included.
-
getOptimizedCriterion
public double getOptimizedCriterion()
Returns the optimized criterion.- Returns:
- A
doublescalar representing the optimized criterion ornullifsolvehas not been called. The criterion to be maximized is a constant plus the log-likelihood.
-
getParameters
public double[][] getParameters()
Returns the parameter estimates and associated statistics.- Returns:
- An
nCoefrow by 4 columndoublematrix containing the parameter estimates and associated statistics ornullifsolvehas not been called. Here,nCoefis the number of coefficients in the model. The statistics returned are as follows:Column Statistic 0 Coefficient estimate. 1 Estimated standard deviation of the estimated coefficient. 2 Asymptotic normal score for testing that the coefficient is zero. 3 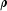 -
value associated with the normal score in column 2.
-
value associated with the normal score in column 2.
-
getProduct
public double[] getProduct() throws CategoricalGenLinModel.ClassificationVariableException, CategoricalGenLinModel.ClassificationVariableLimitException, CategoricalGenLinModel.ClassificationVariableValueException, CategoricalGenLinModel.DeleteObservationsException, CategoricalGenLinModel.RankDeficientException, SVD.DidNotConvergeExceptionReturns the inverse of the Hessian times the gradient vector computed at the input parameter estimates.- Returns:
- A
doublearray of length nCoef containing the inverse of the Hessian times the gradient vector computed at the input parameter estimates. nCoef is the number of coefficients in the model. This member function will callsolveto get the product if the product has not already been computed. - Throws:
CategoricalGenLinModel.ClassificationVariableException- is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1CategoricalGenLinModel.ClassificationVariableLimitException- is thrown when the sum of the number of distinct values taken on by each classification variable exceeds the maximum allowed,maxclCategoricalGenLinModel.DeleteObservationsException- is thrown if the number of observations to be deleted has grown too largeCategoricalGenLinModel.ClassificationVariableValueExceptionCategoricalGenLinModel.RankDeficientExceptionSVD.DidNotConvergeException
-
setCensorColumn
public void setCensorColumn(int icen)
Sets the column number inxwhich contains the interval type for each observation.- Parameters:
icen- Anintscalar which indicates the column numberxwhich contains the interval type code for each observation. The valid codes are interpreted as:
If this member function is not called a censoring code of 0 is assumed.x[i][icen]Censoring 0 Point observation. The response is unique and is given by x[i][irt].1 Right interval. The response is greater than or equal to x[i][irt]and less than or equal to the upper bound, if any, of the distribution.2 Left interval. The response is less than or equal to x[i][ilt]and greater than or equal to the lower bound of the distribution.3 Full interval. The response is greater than or equal to x[i][irt]but less than or equal tox[i][ilt].- Throws:
IllegalArgumentException- is thrown whenicenis less than 0 or greater than or equal to the number of columns ofx
-
setClassificationVariableColumn
public void setClassificationVariableColumn(int[] indcl)
Initializes an index vector to contain the column numbers inxthat are classification variables.- Parameters:
indcl- Anintvector which contains the column numbers inxthat are classification variables. By default this vector is not referenced.- Throws:
IllegalArgumentException- is thrown when an element ofindclis less than 0 or greater than or equal to the number of columns ofx
-
setConvergenceTolerance
public void setConvergenceTolerance(double eps)
Set the convergence criterion.- Parameters:
eps- Adoublescalar specifying the convergence criterion. Convergence is assumed when the maximum relative change in any coefficient estimate is less thanepsfrom one iteration to the next or when the relative change in the log-likelihood,getOptimizedCriterion, from one iteration to the next is less thaneps/100.epsmust be greater than 0. If this member function is not called,eps= .001 is assumed.- Throws:
IllegalArgumentException- is thrown ifepsis or equal to 0
-
setEffects
public void setEffects(int[] indef, int[] nvef)Initializes an index vector to contain the column numbers inxassociated with each effect.- Parameters:
indef- Anintvector of length![sum_{k=0}^{mbox{nef}-1}mbox{nvef[k]}](eqn_3801.png) where
nef is the number of effects in the model.
where
nef is the number of effects in the model.
indefcontains the column numbers inxthat are associated with each effect. Member functionsetEffects(int [], nvef [])sets the number of variables associated with each effect in the model. The firstnvef[0]elements ofindefgive the column numbers of the variables in the first effect. The nextnvef[0]elements give the column numbers of the variables in the second effect, etc. By default this vector is not referenced.nvef- Anintvector of length nef where nef is the number of effects in the model.nvefcontains the number of variables associated with each effect in the model. By default this vector is not referenced.- Throws:
IllegalArgumentException- is thrown when an element ofindefis less than 0 or greater than or equal to the number of columns ofxor if an element ofnvefis less than or equal to 0
-
setExtendedLikelihoodObservations
public void setExtendedLikelihoodObservations(int[] iadds)
Initializes a vector indicating which observations are to be included in the extended likelihood.- Parameters:
iadds- Anintarray of length nobs indicating which observations are included in the extended likelihood where nobs is the number of observations. The values within the array are interpreted as:
If this member function is not called,Value Status of observation 0 Observation i is in the likelihood. 1 Observation i cannot be in the likelihood because it contains at least one missing value in x.2 Observation i is not in the likelihood. Its estimated parameter is infinite. iaddsis set to all zeroes.- Throws:
IllegalArgumentException- is thrown when an element ofiaddsis not in the range [0,2]
-
setFixedParameterColumn
public void setFixedParameterColumn(int ifix)
Sets the column number inxthat contains a fixed parameter for each observation that is added to the linear response prior to computing the model parameter.- Parameters:
ifix- Anintscalar which indicates the column number inxthat contains a fixed parameter for each observation that is added to the linear response prior to computing the model parameter. The "fixed" parameter allows one to test hypothesis about the parameters via the log-likelihoods. By default the fixed parameter is assumed to be zero.- Throws:
IllegalArgumentException- is thrown whenifixis less than 0 or greater than or equal to the number of columns ofx
-
setFrequencyColumn
public void setFrequencyColumn(int ifrq)
Sets the column number inxthat contains the frequency of response for each observation.- Parameters:
ifrq- Anintscalar which indicates the column number inxthat contains the frequency of response for each observation. By default a frequency of 1 for each observation is assumed.- Throws:
IllegalArgumentException- is thrown whenifrqis less than 0 or greater than or equal to the number of columns ofx
-
setInfiniteEstimateMethod
public void setInfiniteEstimateMethod(int infin)
Sets the method to be used for handling infinite estimates.- Parameters:
infin- Anintscalar which indicates the method to be used for handling infinite estimates. The method value is interpreted as follows:
By defaultinfinMethod 0 Remove a right or left-censored observation from the log-likelihood whenever the probability of the observation exceeds 0.995. At convergence, use linear programming to check that all removed observations actually have an estimated linear response that is infinite. Set iadds[i]for observation i to 2 if the linear response is infinite. If not all removed observations have infinite linear response, recompute the estimates based upon the observations with estimated linear response that is finite. This option is valid only for censoring codes 1 and 2.1 Iterate without checking for infinite estimates. infin= 1.- Throws:
IllegalArgumentException- is thrown wheninfinis less than 0 or greater than 1
-
setInitialEstimates
public void setInitialEstimates(int init, double[] estimates)Sets the initial parameter estimates option.- Parameters:
init- An inputintindicating the desired initialization method for the initial estimates of the parameters. If this method is not called,initis set to 0.initAction 0 Unweighted linear regression is used to obtain initial estimates. 1 The nCoef, number of coefficients, elements of estimatescontain initial estimates of the parameters. Use of this option requires that the user know nCoef beforehand.estimates- An inputdoublearray of length nCoef containing the initial estimates of the parameters where nCoef is the number of estimated coefficients in the model. (Used ifinit= 1.) If this member function is not called, unweighted linear regression is used to obtain the initial estimates.- Throws:
IllegalArgumentException- is thrown wheninitis not in the range [0,1]
-
setLowerEndpointColumn
public void setLowerEndpointColumn(int irt)
Sets the column number inxthat contains the lower endpoint of the observation interval for full interval and right interval observations.- Parameters:
irt- Anintscalar which indicates the column number inxthat contains the lower endpoint of the observation interval for full interval and right interval observations. By default all observations are treated as "point" observations andx[i][irt]contains the observation point. If this member function is not called, the last column ofxis assumed to contain the "point" observations.- Throws:
IllegalArgumentException- is thrown whenirtis less than 0 or greater than or equal to the number of columns ofx
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Set the maximum number of iterations allowed.- Parameters:
maxIterations- Anintspecifying the maximum number of iterations allowed.maxIterationsmust be greater than 0. If this member function is not called, the maximum number of iterations is set to 30.- Throws:
IllegalArgumentException- is thrown ifmaxIterationsis less than or equal to 0
-
setModelIntercept
public void setModelIntercept(int intcep)
Sets the intercept option.- Parameters:
intcep- Anintscalar which indicates whether or not the model has an intercept. Inputintcepis interpreted as follows:
By defaultValue Action 0 No intercept is in the model (unless otherwise provided for by the user). 1 Intercept is automatically included in the model. intcep= 1.- Throws:
IllegalArgumentException- is thrown whenintcepis less than 0 or greater than 1
-
setObservationMax
public void setObservationMax(int nmax)
Sets the maximum number of observations that can be handled in the linear programming.- Parameters:
nmax- Anintscalar which sets the maximum number of observations that can be handled in the linear programming. An illegal argument exception is thrown ifnmaxis less than 0. If this member function is not called,nmaxis set to the number of observations.- Throws:
IllegalArgumentException- is thrown whennmaxis less than 0
-
setOptionalDistributionParameterColumn
public void setOptionalDistributionParameterColumn(int ipar)
Sets the column number inxthat contains an optional distribution parameter for each observation.- Parameters:
ipar- Anintscalar which indicates the column number inxthat contains an optional distribution parameter for each observation. The distribution parameter values are interpreted as follows depending on the model chosen:
By default the distribution parameter is assumed to be 1.Model Meaning of x[i][ipar]0 The Poisson parameter is given by ![x[i][ipar]times
{e^rho}](eqn_3800.png) .
.1 The number of successes required in the negative binomial is given by x[i][ipar].2 x[i][ipar] is not used.3-5 The number of trials in the binomial distribution is given by x[i][ipar].- Throws:
IllegalArgumentException- is thrown wheniparis less than 0 or greater than or equal to the number of columns ofx
-
setTolerance
public void setTolerance(double tol)
Initializes the tolerance used in determining linear dependence.- Parameters:
tol- Andoublevalue used in determining linear dependence. When linear dependence is detected, a RankDeficientException is thrown and no results are computed. Computations for a rank deficient model can be forced to continue by specifying a negative tolerance. Iftolis negative, the absolute value oftolwill be used to determine linear dependence, but computations will proceed with warning RankDeficientWarning. In this case the results should be carefully inspected and used with caution. If this member function is not called,tolwill be set to .22204460492503130808e-14.
-
setUpperBound
public void setUpperBound(int maxcl)
Sets the upper bound on the sum of the number of distinct values taken on by each classification variable.- Parameters:
maxcl- Anintscalar specifying the upper bound on the sum of the number of distinct values taken on by each classification variable. If this member function is not called, an upper bound of 1 is used if methodsetClassificationVariableColumnhas not been referenced. Otherwise, the default upper bound is set tonobs * nclvarwherenobsis the number of observations andnclvaris the number of classification variables.- Throws:
IllegalArgumentException- is thrown whenmaxclis less than 1 and the number of classification variables is greater than 0
-
setUpperEndpointColumn
public void setUpperEndpointColumn(int ilt)
Sets the column number inxthat contains the upper endpoint of the observation interval for full interval and left interval observations.- Parameters:
ilt- Anintscalar which indicates the column number inxthat contains the upper endpoint of the observation interval for full interval and left interval observations. By default all observations are treated as "point" observations.- Throws:
IllegalArgumentException- is thrown wheniltis less than 0 or greater than or equal to the number of columns ofx
-
solve
public double[][] solve() throws CategoricalGenLinModel.ClassificationVariableException, CategoricalGenLinModel.ClassificationVariableLimitException, CategoricalGenLinModel.ClassificationVariableValueException, CategoricalGenLinModel.DeleteObservationsException, CategoricalGenLinModel.RankDeficientException, SVD.DidNotConvergeExceptionReturns the parameter estimates and associated statistics for a CategoricalGenLinModel object.- Returns:
- An
nCoefrow by 4 columndoublematrix containing the parameter estimates and associated statistics. Here,nCoefis the number of coefficients in the model. The statistics returned are as follows:Column Statistic 0 Coefficient estimate. 1 Estimated standard deviation of the estimated coefficient. 2 Asymptotic normal score for testing that the coefficient is zero. 3 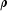 -
value associated with the normal score in column 2.
-
value associated with the normal score in column 2. - Throws:
CategoricalGenLinModel.ClassificationVariableException- is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1CategoricalGenLinModel.ClassificationVariableLimitException- is thrown when the sum of the number of distinct values taken on by each classification variable exceeds the maximum allowed,maxclCategoricalGenLinModel.DeleteObservationsException- is thrown if the number of observations to be deleted has grown too largeCategoricalGenLinModel.ClassificationVariableValueExceptionCategoricalGenLinModel.RankDeficientExceptionSVD.DidNotConvergeException
-
-