- java.lang.Object
-
- com.imsl.stat.Cdf
-
public final class Cdf extends Object
Cumulative probability distribution functions.
-
-
Method Summary
Methods Modifier and Type Method and Description static doublebeta(double x, double pin, double qin)Evaluates the beta cumulative probability distribution function.static doublebetaMean(double pin, double qin)Evaluates the mean of the beta cumulative probability distribution functionstatic doublebetaVariance(double pin, double qin)Evaluates the variance of the beta cumulative probability distribution functionstatic doublebinomial(int k, int n, double pin)Evaluates the binomial cumulative probability distribution function.static doublebivariateNormal(double x, double y, double rho)Evaluates the bivariate normal cumulative probability distribution function.static doublechi(double chsq, double df)Evaluates the chi-squared cumulative distribution function.static doublechiMean(double df)Evaluates the mean of the chi-squared cumulative probability distribution functionstatic doublechiVariance(double df)Evaluates the variance of the chi-squared cumulative probability distribution functionstatic doublecomplementaryChi(double chsq, double df)Calculates the complement of the chi-squared cumulative distribution function.static doublecomplementaryF(double x, double dfn, double dfd)Calculates the complement of the F distribution function.static doublecomplementaryF2(double x, double dfn, double dfd)static doublecomplementaryNoncentralF(double f, double df1, double df2, double lambda)Calculates the complement of the noncentral F cumulative distribution function.static doublecomplementaryStudentsT(double t, double df)Calculates the complement of the Student's t distribution.static doublediscreteUniform(int x, int n)Evaluates the discrete uniform cumulative probability distribution function.static doubleexponential(double x, double scale)Evaluates the exponential cumulative probability distribution function.static doubleextremeValue(double x, double mu, double beta)Evaluates the extreme value cumulative probability distribution function.static doubleF(double x, double dfn, double dfd)Evaluates the F cumulative probability distribution function.static doublegamma(double x, double a)Evaluates the gamma cumulative probability distribution function.static doublegeometric(int x, double pin)Evaluates the discrete geometric cumulative probability distribution function.static doublehypergeometric(int k, int sampleSize, int defectivesInLot, int lotSize)Evaluates the hypergeometric cumulative probability distribution function.static doublelogistic(double x, double mu, double s)Evaluates the logistic cumulative probability distribution function.static doublelogNormal(double x, double mu, double sigma)Evaluates the standard lognormal cumulative probability distribution function.static doublenoncentralBeta(double x, double shape1, double shape2, double lambda)Evaluates the noncentral beta cumulative distribution function (CDF).static doublenoncentralchi(double chsq, double df, double alam)Evaluates the noncentral chi-squared cumulative probability distribution function.static doublenoncentralF(double f, double df1, double df2, double lambda)Evaluates the noncentral F cumulative distribution function.static doublenoncentralstudentsT(double t, int idf, double delta)Evaluates the noncentral Student's t cumulative probability distribution function.static doublenormal(double x)Evaluates the normal (Gaussian) cumulative probability distribution function.static doublePareto(double x, double xm, double k)Evaluates the Pareto cumulative probability distribution function.static doublepoisson(int k, double theta)Evaluates the Poisson cumulative probability distribution function.static doubleRayleigh(double x, double alpha)Evaluates the Rayleigh cumulative probability distribution function.static doublestudentsT(double t, double df)Evaluates the Student's t cumulative probability distribution function.static doubleuniform(double x, double aa, double bb)Evaluates the uniform cumulative probability distribution function.static doubleWeibull(double x, double gamma, double alpha)Evaluates the Weibull cumulative probability distribution function.
-
-
-
Method Detail
-
beta
public static double beta(double x, double pin, double qin)Evaluates the beta cumulative probability distribution function.Method
betaevaluates the distribution function of a beta random variable with parameterspinandqin. This function is sometimes called the incomplete beta ratio and, with p =pinand q =qin, is denoted by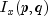 . It is given by
. It is given by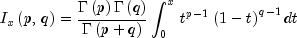
where
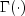 is the gamma function. The
value of the distribution function
is the gamma function. The
value of the distribution function 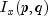 is the
probability that the random variable takes a value less than or equal to
x.
is the
probability that the random variable takes a value less than or equal to
x.The integral in the expression above is called the incomplete beta function and is denoted by
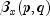 . The
constant in the expression is the reciprocal of the beta function
(the incomplete beta function evaluated at x=1) and is denoted by
. The
constant in the expression is the reciprocal of the beta function
(the incomplete beta function evaluated at x=1) and is denoted by
 .
.betauses the method of Bosten and Battiste (1974).
- Parameters:
x- adouble, the argument at which the function is to be evaluated.pin- adouble, the first beta distribution parameter.qin- adouble, the second beta distribution parameter.- Returns:
- a
double, the probability that a beta random variable takes on a value less than or equal tox. - See Also:
- Example
-
betaMean
public static double betaMean(double pin, double qin)Evaluates the mean of the beta cumulative probability distribution function- Parameters:
pin- adouble, the first beta distribution parameter.qin- adouble, the second beta distribution parameter.- Returns:
- a
double, the mean of the beta distribution function.
-
betaVariance
public static double betaVariance(double pin, double qin)Evaluates the variance of the beta cumulative probability distribution function- Parameters:
pin- adouble, the first beta distribution parameter.qin- adouble, the second beta distribution parameter.- Returns:
- a
double, the variance of the beta distribution function.
-
binomial
public static double binomial(int k, int n, double pin)Evaluates the binomial cumulative probability distribution function.Method
binomialevaluates the distribution function of a binomial random variable with parameters n and p with p=pin. It does this by summing probabilities of the random variable taking on the specific values in its range. These probabilities are computed by the recursive relationship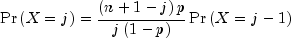
To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than n times p, and are computed backward from n, otherwise. The smallest positive machine number,
 ,
is used as the starting value for summing the probabilities, which are
rescaled by
,
is used as the starting value for summing the probabilities, which are
rescaled by 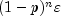 if forward
computation is performed and by
if forward
computation is performed and by  if
backward computation is done. For the special case of
p = 0,
if
backward computation is done. For the special case of
p = 0, binomialis set to 1; and for the case p = 1,binomialis set to 1 if k = n and to 0 otherwise.- Parameters:
k- theintargument for which the binomial distribution function is to be evaluated.n- theintnumber of Bernoulli trials.pin- adoublescalar value representing the probability of success on each independent trial.- Returns:
- a
doublescalar value representing the probability that a binomial random variable takes a value less than or equal tok. This value is the probability thatkor fewer successes occur innindependent Bernoulli trials, each of which has apinprobability of success. - See Also:
- Example
-
bivariateNormal
public static double bivariateNormal(double x, double y, double rho)Evaluates the bivariate normal cumulative probability distribution function. Let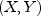 be a bivariate normal variable with
mean
be a bivariate normal variable with
mean 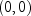 and variance-covariance matrix
and variance-covariance matrix
This method computes the probability that![left[ begin{array}{cc} 1 & rho \ rho & 1end{array}right]](eqn_3468.png)
 and
and
 .
.
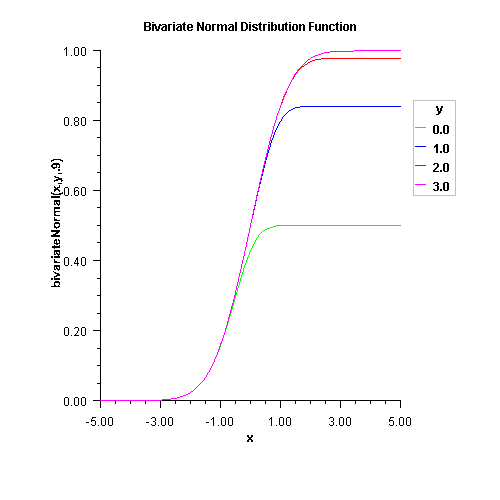
- Parameters:
x- is the x-coordinate of the point for which the bivariate normal distribution function is to be evaluated.y- is the y-coordinate of the point for which the bivariate normal distribution function is to be evaluated.rho- is the correlation coefficient.- Returns:
- the probability that a bivariate normal random variable
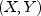 with correlation
with correlation rhosatisfies and
and
 .
.
-
chi
public static double chi(double chsq, double df)Evaluates the chi-squared cumulative distribution function.Method
chievaluates the cumulative distribution function (CDF) F, of a chi-squared random variable withdfdegrees of freedom, that is, with x =chsqand =
= df,
where
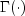 is the gamma function. The
value
is the gamma function. The
value 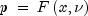 is
the probability that the random variable takes a value less than or
equal to x.
is
the probability that the random variable takes a value less than or
equal to x.For
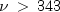 ,
, chiuses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, equation 26.4.17) for p in terms of the normal CDF, which is evaluated using methodnormal.For
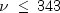 ,
, chiuses series expansions to evaluate p: for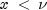 ,
,
chicalculates p using A&S equation 6.5.29, and for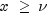 ,
, chicalculates p using the continued fraction (CF) expansion of the incomplete gamma function given in A&S equation 6.5.31 and implemented using Lentz's algorithm (Lentz, W.J., 1976, Applied Optics, vol. 15, pp. 668-671) as modified by Thompson & Barnett (Thompson, I.J., and Barnett, A.R., 1986, Journal of Computational Physics, vol. 64, pp. 490-509).For greater right tail accuracy, see
complementaryChi(double, double).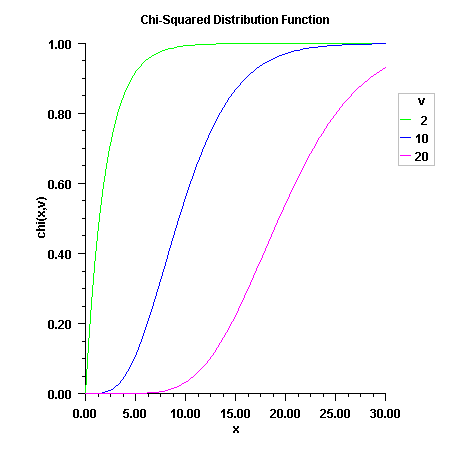
- Parameters:
chsq- adoublescalar value representing the argument at which the function is to be evaluated.df- adoublescalar value representing the number of degrees of freedom.dfmust be positive.- Returns:
- a
doublescalar value representing the probability that a chi-squared random variable takes a value less than or equal tochsq. - See Also:
- Example
-
chiMean
public static double chiMean(double df)
Evaluates the mean of the chi-squared cumulative probability distribution function- Parameters:
df- adoublescalar value representing the number of degrees of freedom. This must be at least 0.5.- Returns:
- a
double, the mean of the chi-squared distribution function.
-
chiVariance
public static double chiVariance(double df)
Evaluates the variance of the chi-squared cumulative probability distribution function- Parameters:
df- adoublescalar value representing the number of degrees of freedom. This must be at least 0.5.- Returns:
- a
double, the variance of the chi-squared distribution function.
-
complementaryChi
public static double complementaryChi(double chsq, double df)Calculates the complement of the chi-squared cumulative distribution function.Method
complementaryChievaluates the cumulative distribution function,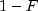 , of a chi-squared random variable with
, of a chi-squared random variable with
dfdegrees of freedom, that is, with x =chsqand =
= df,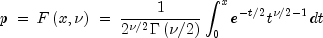
where
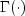 is the gamma function.
The value of the
is the gamma function.
The value of the complementaryChidistribution function at the point x,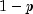 , is the probability that
the random variable takes a value greater than x.
, is the probability that
the random variable takes a value greater than x.For
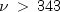 ,
, complementaryChiuses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, equation 26.4.17) for p in terms of the normal CDF, which is evaluated using methodnormal.For
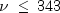 ,
, complementaryChiuses series expansions to evaluate p: for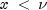 ,
,
complementaryChicalculates p using A&S series 6.5.29, and for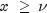 ,
, complementaryChicalculates p using the continued fraction expansion of the incomplete gamma function given in A&S equation 6.5.31 and implemented using Lentz's algorithm (Lentz, W.J., 1976, Applied Optics, vol. 15, pp. 668-671) as modified by Thompson & Barnett (Thompson, I.J., and Barnett, A.R., 1986, Journal of Computational Physics, vol. 64, pp. 490-509).complementaryChiprovides greater right tail accuracy for the Chi-squared distribution than does1 - chi.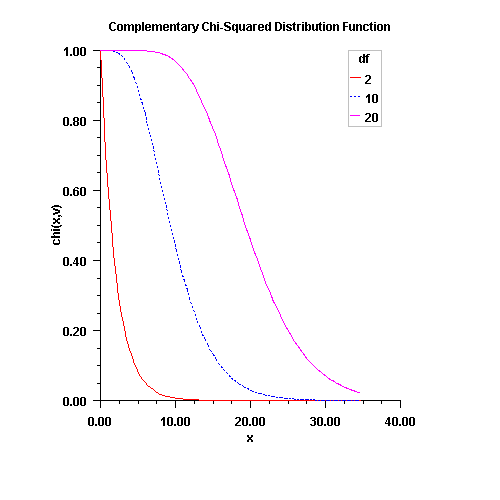
- Parameters:
chsq- adoublescalar value at which the function is to be evaluated.df- adoublescalar value representing the number of degrees of freedom.dfmust be positive.- Returns:
- a
doublescalar value representing the probability that a chi-squared random variable takes a value greater thanchsq.
-
complementaryF
public static double complementaryF(double x, double dfn, double dfd)Calculates the complement of the F distribution function.complementaryFevaluates one minus the distribution function of a Snedecor's F random variable withdfnnumerator degrees of freedom anddfddenominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using the functionbeta. If X is an F variate with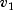 and
and
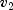 degrees of freedom and
degrees of freedom and
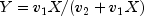 , then Y
is a beta variate with parameters
, then Y
is a beta variate with parameters 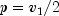 and
and
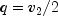 .
. complementaryFalso uses a relationship between F random variables that can be expressed as follows: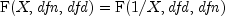
This function provides higher right tail accuracy for the F distribution.

- Parameters:
x- adouble, the argument at which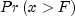 is to be
evaluated.
is to be
evaluated.dfn- adouble, the numerator degrees of freedom. It must be positive.dfd- adouble, the denominator degrees of freedom. It must be positive.- Returns:
- a
double, the probability that an F random variable takes on a value greater thanx.
-
complementaryF2
public static double complementaryF2(double x, double dfn, double dfd)
-
complementaryNoncentralF
public static double complementaryNoncentralF(double f, double df1, double df2, double lambda)Calculates the complement of the noncentral F cumulative distribution function.The complementary noncentral F distribution is a generalization of the complementary F distribution. If
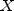 is a
noncentral chi-square random variable with noncentrality parameter
is a
noncentral chi-square random variable with noncentrality parameter
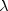 and
and 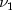 degrees of
freedom, and
degrees of
freedom, and  is a chi-square random variable with
is a chi-square random variable with
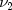 degrees of freedom which is statistically
independent of
degrees of freedom which is statistically
independent of  , then
, then
is a noncentral F-distributed random variable whose CDF is given by: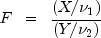
where: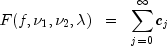
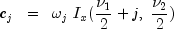
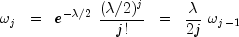
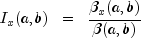
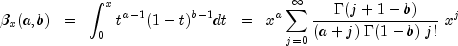
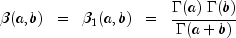
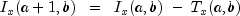
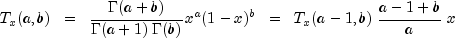
and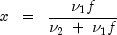
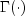 is the gamma function,
is the gamma function,
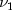 =
= df1,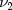 =
= df2, =
= lambda, and f =f. The above series expansion for the noncentral F was taken from Butler and Paolella (1999) (see Paolella.pdf), with the correction for the recursion relation given below:
extracted from the AS 63 algorithm for calculating the incomplete beta function as described by Majumder and Bhattacharjee (1973). The series approximation of the complementary (cmp) noncentral F CDF, denoted by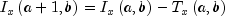
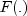 , is obtainable by
using the following identities:
, is obtainable by
using the following identities:
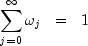
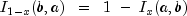
Thus:
We can use the above expansion of![begin{array}{ll}
overline{F}(f, nu_1, nu_2, lambda) ;; & displaystyle = ;; 1 ;;
- ;; sum_{j = 0}^infty {c_j} ;; = ;; sum_{j = 0}^infty
{omega_j[1 ; - ; I_x (frac{nu_1}{2} + j, ; frac{nu_2}{2})]} ;; \
& displaystyle = ;; sum_{j = 0}^infty {omega_j ; I_{1-x}
(frac{nu_2}{2}, ; frac{nu_1}{2} + j)}
end{array}](eqn_3706.png)
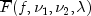 and the identities:
and the identities:

to recursively calculate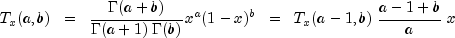
 .
.
With a noncentrality parameter of zero, the noncentral F distribution is the same as the F distribution.
- Parameters:
f- adoublevalue representing the argument at which the function is to be evaluated.fmust be nonnegative.df1- adoublevalue representing the number of numerator degrees of freedom.df1must be positive.df2- adoublevalue representing the number of denominator degrees of freedom.df2must be positive.lambda- adoublevalue representing the noncentrality parameter.lambdamust be nonnegative.- Returns:
- a
doublescalar value representing the probability that a noncentral F random variable takes a value greater thanf.
-
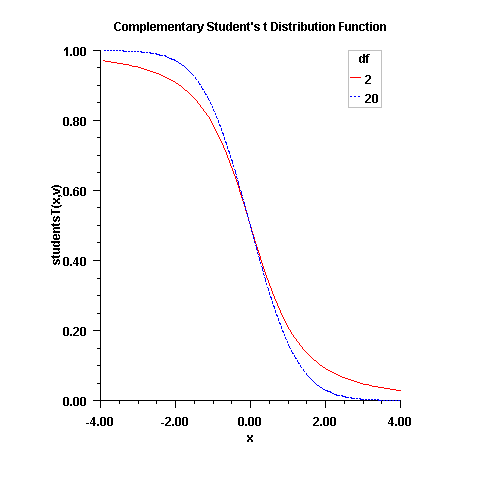
complementaryStudentsT
public static double complementaryStudentsT(double t, double df)Calculates the complement of the Student's t distribution.Method
complementaryStudentsTevaluates one minus the distribution function of a Student's t random variable withdfdegrees of freedom. If the square of t is greater than or equal todf, the relationship of a t to an f random variable (and subsequently, to a beta random variable) is exploited, and routinebetais used. Otherwise, the method described by Hill (1970) is used. Ifdfis not an integer, ifdfis greater than 19, or ifdfis greater than 200, a Cornish-Fisher expansion is used to evaluate the distribution function. Ifdfis less than 20 and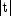 is less than
2.0, a trigonometric series (see Abramowitz and
Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is
used. For the remaining cases, a series given by Hill (1970) that
converges well for large values of
is less than
2.0, a trigonometric series (see Abramowitz and
Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is
used. For the remaining cases, a series given by Hill (1970) that
converges well for large values of tis used.This function provides higher right tail accuracy for the Student's t distribution.
- Parameters:
t- adoublescalar value for which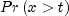 is to be evaluated
is to be evaluateddf- adoublescalar value representing the number of degrees of freedom. This must be at least one.- Returns:
- a
doublescalar value representing the probability that a Student's t random variable takes a value greater thant. - See Also:
- Example
-
discreteUniform
public static double discreteUniform(int x, int n)Evaluates the discrete uniform cumulative probability distribution function.- Parameters:
x- anintscalar value representing the argument at which the function is to be evaluated.xshould be a value between the lower limit 0 and upper limitnn- anintscalar value representing the upper limit of the discrete uniform distribution.- Returns:
- a
doublescalar value representing the probability that a discrete uniform random variable takes a value less than or equal tox.
-
exponential
public static double exponential(double x, double scale)Evaluates the exponential cumulative probability distribution function.Method
exponentialis a special case of the gamma distribution function, which evaluates the distribution function, F, with scale parameter b and shape parameter a, used in the gamma distribution function equal to 1.0. That is,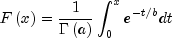
where
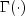 is the gamma function.
(The gamma function is the integral from
0 to
is the gamma function.
(The gamma function is the integral from
0 to  of the same integrand as
above). The value of the distribution function at the point
x is the probability that the random variable takes
a value less than or equal to x.
of the same integrand as
above). The value of the distribution function at the point
x is the probability that the random variable takes
a value less than or equal to x.If
xis less than or equal to 1.0,gammauses a series expansion. Otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.scale- adoublescalar value representing the scale parameter,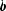 .
.- Returns:
- a
doublescalar value representing the probability that an exponential random variable takes on a value less than or equal tox. - See Also:
- Example
-
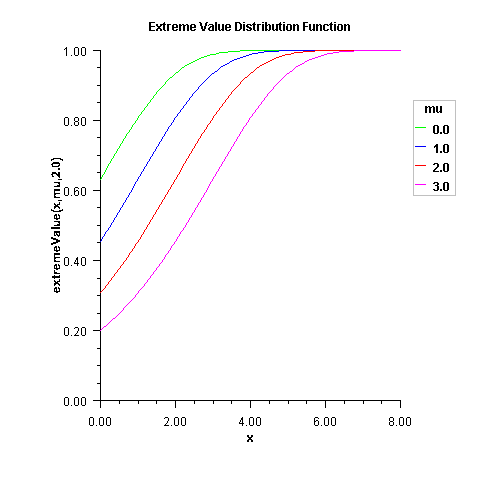
extremeValue
public static double extremeValue(double x, double mu, double beta)Evaluates the extreme value cumulative probability distribution function.Method
extremeValue, also known as the Gumbel minimum distribution, evaluates the extreme value distribution function, F, of a uniform random variable with location parameter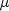 and shape parameter
and shape parameter 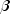 ; that is,
; that is,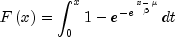
The case where
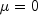 and
and
 is called the standard
Gumbel distribution.
is called the standard
Gumbel distribution.Random numbers are generated by evaluating uniform variates
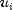 , equating the continuous distribution function,
and then solving for
, equating the continuous distribution function,
and then solving for 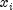 by first computing
by first computing
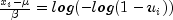 .
.
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.mu- adoublescalar value representing the location parameter, .
.beta- adoublescalar value representing the scale parameter,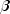
- Returns:
- a
doublescalar value representing the probability that an extreme value random variable takes on a value less than or equal tox. - See Also:
- Example
-
F
public static double F(double x, double dfn, double dfd)Evaluates the F cumulative probability distribution function.Fevaluates the distribution function of a Snedecor's F random variable withdfnnumerator degrees of freedom anddfddenominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using the functionbeta. If X is an F variate with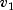 and
and
 degrees of freedom and
degrees of freedom and
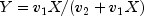 , then Y
is a beta variate with parameters
, then Y
is a beta variate with parameters 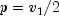 and
and
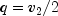 .
. Falso uses a relationship between F random variables that can be expressed as follows: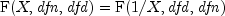
For greater right tail accuracy, see
complementaryF(double, double, double).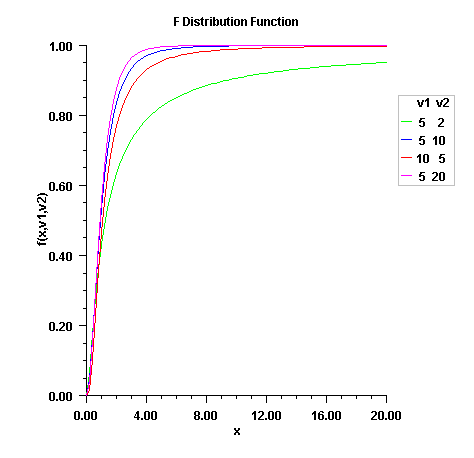
- Parameters:
x- adouble, the argument at which the function is to be evaluated.dfn- adouble, the numerator degrees of freedom. It must be positive.dfd- adouble, the denominator degrees of freedom. It must be positive.- Returns:
- a
double, the probability that an F random variable takes on a value less than or equal tox. - See Also:
- Example
-
gamma
public static double gamma(double x, double a)Evaluates the gamma cumulative probability distribution function.Method
gammaevaluates the distribution function, F, of a gamma random variable with shape parameter a; that is,
where
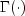 is the gamma function.
(The gamma function is the integral from
0 to
is the gamma function.
(The gamma function is the integral from
0 to  of the same integrand as
above). The value of the distribution function at the point
x is the probability that the random variable takes
a value less than or equal to x.
of the same integrand as
above). The value of the distribution function at the point
x is the probability that the random variable takes
a value less than or equal to x.The gamma distribution is often defined as a two-parameter distribution with a scale parameter b (which must be positive), or even as a three-parameter distribution in which the third parameter c is a location parameter. In the most general case, the probability density function over
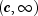 is
is
If T is such a random variable with parameters a, b, and c, the probability that
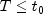 can be obtained from
can be obtained from
gammaby setting .
.If X is less than a or if X is less than or equal to 1.0,
gammauses a series expansion. Otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.a- adoublescalar value representing the shape parameter. This must be positive.- Returns:
- a
doublescalar value representing the probability that a gamma random variable takes on a value less than or equal tox. - See Also:
- Example
-
geometric
public static double geometric(int x, double pin)Evaluates the discrete geometric cumulative probability distribution function.- Parameters:
x- anintscalar value representing the argument at which the function is to be evaluatedpin- andoublescalar value representing the probability parameter for each independent trial (the probability of success for each independent trial).- Returns:
- a
doublescalar value representing the probability that a geometric random variable takes a value less than or equal tox. The return value is the probability that up toxtrials would be observed before observing a success.
-
hypergeometric
public static double hypergeometric(int k, int sampleSize, int defectivesInLot, int lotSize)Evaluates the hypergeometric cumulative probability distribution function.Method
hypergeometricevaluates the distribution function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable X can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is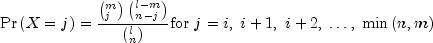
where
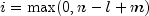 .
.If k is greater than or equal to i and less than or equal to
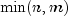 ,
,
hypergeometricsums the terms in this expression for j going from i up to k. Otherwise,hypergeometricreturns 0 or 1, as appropriate. So, as to avoid rounding in the accumulation,hypergeometricperforms the summation differently depending on whether or not k is greater than the mode of the distribution, which is the greatest integer less than or equal to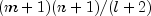 .
.- Parameters:
k- anint, the argument at which the function is to be evaluated.sampleSize- anint, the sample size,n.defectivesInLot- anint, the number of defectives in the lot,m.lotSize- anint, the lot size,l.- Returns:
- a
double, the probability that a hypergeometric random variable takes a value less than or equal tok. - See Also:
- Example
-
logistic
public static double logistic(double x, double mu, double s)Evaluates the logistic cumulative probability distribution function.Method
logisticevaluates the distribution function, F, of a logistic random variable with location parameter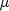 and
scale parameter s. It is given by
and
scale parameter s. It is given by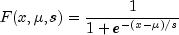
where
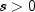 .
.- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.mu- adoublescalar value representing the location parameter,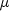 .
.s- adoublescalar value representing the scale parameter.- Returns:
- a
doublescalar value representing the probability that a logistic random variable takes a value less than or equal tox.
-
logNormal
public static double logNormal(double x, double mu, double sigma)Evaluates the standard lognormal cumulative probability distribution function.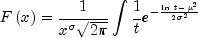
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.mu- adoublescalar value representing the location parameter.sigma- adoublescalar value representing the shape parameter.sigmamust be a positive.- Returns:
- a
doublescalar value representing the probability that a standard lognormal random variable takes a value less than or equal tox.
-
noncentralBeta
public static double noncentralBeta(double x, double shape1, double shape2, double lambda)Evaluates the noncentral beta cumulative distribution function (CDF).The noncentral beta distribution is a generalization of the beta distribution. If
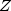 is a noncentral chi-square
random variable with noncentrality parameter
is a noncentral chi-square
random variable with noncentrality parameter 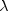 and
and  degrees of freedom, and
degrees of freedom, and
 is a chi-square random variable with
is a chi-square random variable with 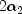 degrees of freedom which is statistically
independent of
degrees of freedom which is statistically
independent of 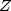 , then
, then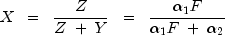
is a noncentral beta-distributed random variable and
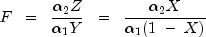
is a noncentral F-distributed random variable. The CDF for noncentral beta variable X can thus be simply defined in terms of the noncentral F CDF:
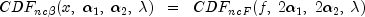
where
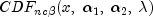 is the noncentral beta CDF with
is the noncentral beta CDF with  =
= x,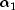 =
= shape1,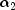 =
= shape2, and noncentrality parameter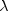 =
= lambda; is the noncentral F CDF
with argument f, numerator and denominator degrees of freedom
is the noncentral F CDF
with argument f, numerator and denominator degrees of freedom 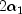 and
and 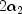 respectively, and noncentrality parameter
respectively, and noncentrality parameter 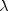 ; and:
; and: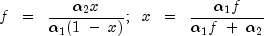
(See documentation for class
CdfmethodnoncentralFfor a discussion of how the noncentral F CDF is defined and calculated.)With a noncentrality parameter of zero, the noncentral beta distribution is the same as the beta distribution.
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.xmust be nonnegative and less than or equal to 1.shape1- adoublescalar value representing the first shape parameter.shape1must be positive.shape2- adoublescalar value representing the second shape parameter.shape2must be positive.lambda- adoublescalar value representing the noncentrality parameter.lambdamust nonnegative.- Returns:
- a
doublescalar value representing the probability that a noncentral beta random variable takes a value less than or equal tox.
-
noncentralchi
public static double noncentralchi(double chsq, double df, double alam)Evaluates the noncentral chi-squared cumulative probability distribution function.Method
noncentralchievaluates the distribution function, F, of a noncentral chi-squared random variable withdfdegrees of freedom and noncentrality parameteralam, that is, with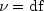 ,
, 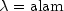 , and
, and 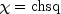 ,
,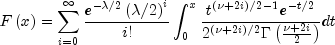
where
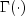 is the gamma function. This is a series of central
chi-squared distribution functions with Poisson weights.
The
value of the distribution function at the point x is
the probability that the random variable takes a value less than or
equal to x.
is the gamma function. This is a series of central
chi-squared distribution functions with Poisson weights.
The
value of the distribution function at the point x is
the probability that the random variable takes a value less than or
equal to x.The noncentral chi-squared random variable can be defined by the distribution function above, or alternatively and equivalently, as the sum of squares of independent normal random variables. If the
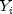 have independent normal distributions with means
have independent normal distributions with means
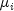 and variances equal to one and
and variances equal to one and 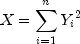
then
 has a noncentral chi-squared distribution with
has a noncentral chi-squared distribution with  degrees of freedom and noncentrality parameter equal to
degrees of freedom and noncentrality parameter equal to 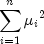
With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the chi-squared distribution.
noncentralchidetermines the point at which the Poisson weight is greatest, and then sums forward and backward from that point, terminating when the additional terms are sufficiently small or when a maximum of 1000 terms have been accumulated. The recurrence relation 26.4.8 of Abramowitz and Stegun (1964) is used to speed the evaluation of the central chi-squared distribution functions.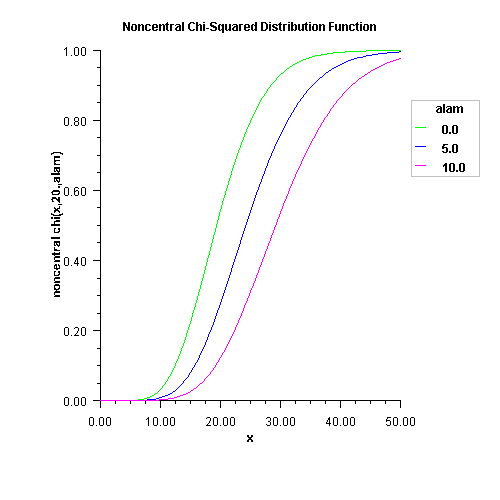
- Parameters:
chsq- adoublescalar value representing the argument at which the function is to be evaluated.df- adoublescalar value representing the number of degrees of freedom.dfmust be positive.alam- adoublescalar value representing the noncentrality parameter. This must be nonnegative, andalam + dfmust be less than or equal to 200,000.- Returns:
- a
doublescalar value representing the probability that a chi-squared random variable takes a value less than or equal tochsq. - See Also:
- Example
-
noncentralF
public static double noncentralF(double f, double df1, double df2, double lambda)Evaluates the noncentral F cumulative distribution function.The noncentral F distribution is a generalization of the F distribution. If
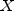 is a noncentral chi-square
random variable with noncentrality parameter
is a noncentral chi-square
random variable with noncentrality parameter 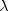 and
and 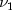 degrees of freedom, and
degrees of freedom, and
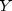 is a chi-square random variable with
is a chi-square random variable with
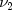 degrees of freedom which is statistically
independent of
degrees of freedom which is statistically
independent of 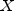 , then
, then
is a noncentral F-distributed random variable whose CDF is given by:
where: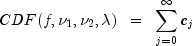
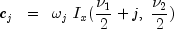

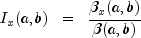
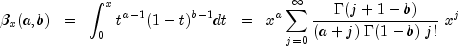

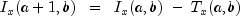

and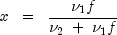
 is the gamma function,
is the gamma function,
 =
= df1,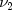 =
= df2, =
= lambda, and f =f.With a noncentrality parameter of zero, the noncentral F distribution is the same as the F distribution.
- Parameters:
f- adoublevalue representing the argument at which the function is to be evaluated.fmust be nonnegative.df1- adoublevalue representing the number of numerator degrees of freedom.df1must be positive.df2- adoublevalue representing the number of denominator degrees of freedom.df2must be positive.lambda- adoublevalue representing the noncentrality parameter.lambdamust be nonnegative.- Returns:
- a
doublescalar value representing the probability that a noncentral F random variable takes a value less than or equal tof.
-
noncentralstudentsT
public static double noncentralstudentsT(double t, int idf, double delta)Evaluates the noncentral Student's t cumulative probability distribution function.Method
noncentralstudentsTevaluates the distribution functionFof a noncentral t random variable withidfdegrees of freedom and noncentrality parameterdelta; that is, with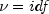 ,
, 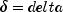 , and
, and 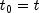 ,
, 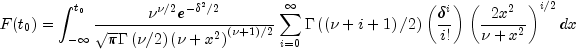
where
 is the gamma function. The
value of the distribution function at the point
is the gamma function. The
value of the distribution function at the point 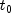 is
the probability that the random variable takes a value less than or
equal to
is
the probability that the random variable takes a value less than or
equal to 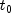 .
.The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi-squared random variable. If w has a normal distribution with mean
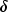 and variance equal to one,
and variance equal to one,  has
an independent chi-squared distribution with
has
an independent chi-squared distribution with  degrees of freedom, and
degrees of freedom, and 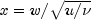
then
 has a noncentral
has a noncentral 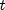 distribution with
distribution with  degrees of
freedom and noncentrality parameter
degrees of
freedom and noncentrality parameter 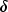 .
.The distribution function of the noncentral
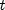 can also be expressed as a
double integral involving a normal density function (see, for example, Owen 1962, page 108). The method
can also be expressed as a
double integral involving a normal density function (see, for example, Owen 1962, page 108). The method
noncentralstudentsTuses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.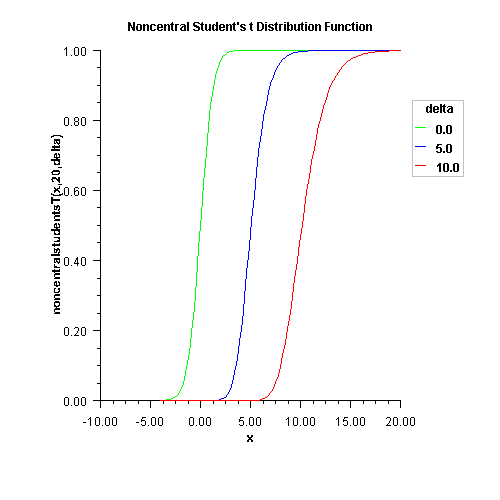
- Parameters:
t- adoublescalar value representing the argument at which the function is to be evaluated.idf- anintscalar value representing the number of degrees of freedom. This must be positive.delta- adoublescalar value representing the noncentrality parameter.- Returns:
- a
doublescalar value representing the probability that a noncentral Student's t random variable takes a value less than or equal tot. - See Also:
- Example
-
normal
public static double normal(double x)
Evaluates the normal (Gaussian) cumulative probability distribution function.Method
normalevaluates the distribution function,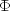 , of a standard normal (Gaussian) random
variable, that is,
, of a standard normal (Gaussian) random
variable, that is,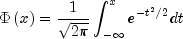
The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
The standard normal distribution (for which
normalis the distribution function) has mean of 0 and variance of 1. The probability that a normal random variable with mean and variance
and variance
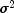 is less than y
is given by
is less than y
is given by normalevaluated at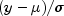 .
. 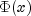 is evaluated by use of the complementary
error function, erfc. The relationship is:
is evaluated by use of the complementary
error function, erfc. The relationship is: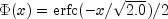
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.- Returns:
- a
doublescalar value representing the probability that a normal variable takes a value less than or equal tox. - See Also:
- Example
-
Pareto
public static double Pareto(double x, double xm, double k)Evaluates the Pareto cumulative probability distribution function.Method
Paretoevaluates the distribution function, F, of a Pareto random variable with scale parameter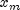 and
shape parameter k. It is given by
and
shape parameter k. It is given by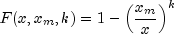
where
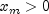 and
and 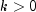 . The function is
only defined for
. The function is
only defined for 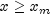
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.xm- adoublescalar value representing the scale parameter,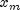 .
.k- adoublescalar value representing the shape parameter, .
.- Returns:
- a
doublescalar value representing the probability that a Pareto random variable takes a value less than or equal tox.
-
poisson
public static double poisson(int k, double theta)Evaluates the Poisson cumulative probability distribution function.poissonevaluates the distribution function of a Poisson random variable with parametertheta.theta, which is the mean of the Poisson random variable, must be positive. The probability function (with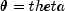 ) is
) is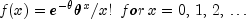
The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed.
poissonuses the recursive relationship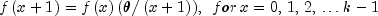
with
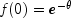 .
.- Parameters:
k- theintargument for which the Poisson distribution function is to be evaluated.theta- adoublescalar value representing the mean of the Poisson distribution.- Returns:
- a
doublescalar value representing the probability that a Poisson random variable takes a value less than or equal to k. - See Also:
- Example
-
Rayleigh
public static double Rayleigh(double x, double alpha)Evaluates the Rayleigh cumulative probability distribution function.Method
Rayleighis a special case of Weibull distribution function where the shape parametergammais 2.0; that is,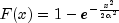
where
alphais the scale parameter.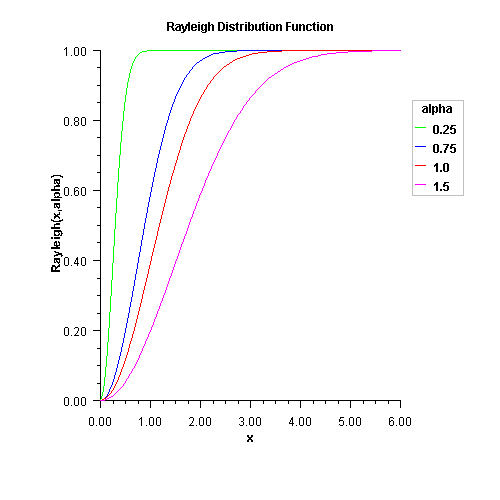
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated. It must be non-negative.alpha- adoublescalar value representing the scale parameter.- Returns:
- a
doublescalar value representing the probability that a Rayleigh random variable takes a value less than or equal tox.
-
studentsT
public static double studentsT(double t, double df)Evaluates the Student's t cumulative probability distribution function.Method
studentsTevaluates the distribution function of a Student's t random variable withdfdegrees of freedom. If the square of t is greater than or equal todf, the relationship of a t to an f random variable (and subsequently, to a beta random variable) is exploited, and routinebetais used. Otherwise, the method described by Hill (1970) is used. Ifdfis not an integer, ifdfis greater than 19, or ifdfis greater than 200, a Cornish-Fisher expansion is used to evaluate the distribution function. Ifdfis less than 20 and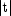 is less than
2.0, a trigonometric series (see Abramowitz and
Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is
used. For the remaining cases, a series given by Hill (1970) that
converges well for large values of
is less than
2.0, a trigonometric series (see Abramowitz and
Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is
used. For the remaining cases, a series given by Hill (1970) that
converges well for large values of tis used.For greater right tail accuracy, see
complementaryStudentsT(double, double).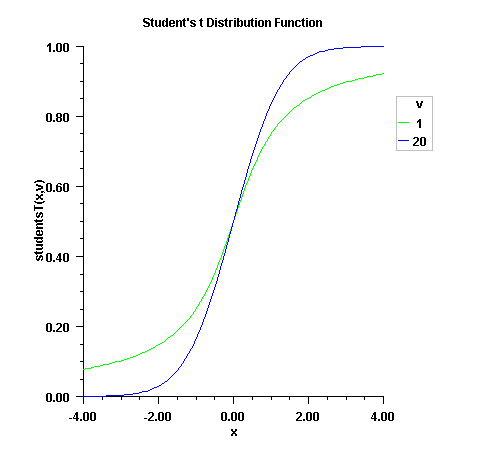
- Parameters:
t- adoublescalar value representing the argument at which the function is to be evaluateddf- adoublescalar value representing the number of degrees of freedom. This must be at least one.- Returns:
- a
doublescalar value representing the probability that a Student's t random variable takes a value less than or equal tot. - See Also:
- Example
-
uniform
public static double uniform(double x, double aa, double bb)Evaluates the uniform cumulative probability distribution function.Method
uniformevaluates the distribution function, F, of a uniform random variable with location parameter aa and scale parameter bb; that is,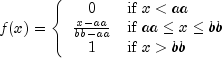

- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated.aa- adoublescalar value representing the location parameter.bb- adoublescalar value representing the scale parameter.- Returns:
- a
doublescalar value representing the probability that a uniform random variable takes a value less than or equal tox.
-
Weibull
public static double Weibull(double x, double gamma, double alpha)Evaluates the Weibull cumulative probability distribution function.Method
Weibullevaluates the distribution function given by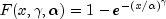
- Parameters:
x- adoublescalar value representing the argument at which the function is to be evaluated. It must be non-negative.gamma- adoublescalar value representing the shape parameter,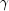 .
.alpha- adoublescalar value representing the scale parameter, .
.- Returns:
- a
doublescalar value representing the probability that a Weibull random variable takes a value less than or equal tox.
-
-