- java.lang.Object
-
- com.imsl.stat.ContingencyTable
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class ContingencyTable extends Object implements Serializable, Cloneable
Performs a chi-squared analysis of a two-way contingency table.Class
ContingencyTablecomputes statistics associated with an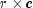 contingency table. The function computes
the chi-squared test of independence, expected values, contributions to
chi-squared, row and column marginal totals, some measures of association,
correlation, prediction, uncertainty, the McNemar test for symmetry, a test
for linear trend, the odds and the log odds ratio, and the kappa statistic
(if the appropriate optional arguments are selected).
contingency table. The function computes
the chi-squared test of independence, expected values, contributions to
chi-squared, row and column marginal totals, some measures of association,
correlation, prediction, uncertainty, the McNemar test for symmetry, a test
for linear trend, the odds and the log odds ratio, and the kappa statistic
(if the appropriate optional arguments are selected).Notation
Let
 denote the observed cell frequency in the
ij cell of the table and n denote the total count in the
table. Let
denote the observed cell frequency in the
ij cell of the table and n denote the total count in the
table. Let 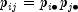 denote the
predicted cell probabilities under the null hypothesis of independence,
where
denote the
predicted cell probabilities under the null hypothesis of independence,
where 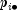 and
and 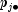 are the row and column marginal relative frequencies. Next, compute the
expected cell counts as
are the row and column marginal relative frequencies. Next, compute the
expected cell counts as 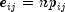 .
.Also required in the following are
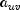 and
and
 for
for  .
Let
.
Let 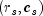 denote the row and column response of
observation s. Then,
denote the row and column response of
observation s. Then,  , or
-1, depending on whether
, or
-1, depending on whether
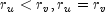 , or
, or 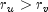 ,
respectively. The
,
respectively. The 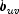 are similarly defined in terms
of the
are similarly defined in terms
of the 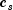 variables.
variables.Chi-squared Statistic
For each cell in the table, the contribution to
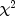 is given as
is given as  . The Pearson
chi-squared statistic (denoted
. The Pearson
chi-squared statistic (denoted 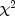 ) is computed as
the sum of the cell contributions to chi-squared. It has
(r - 1) (c - 1) degrees of freedom and tests the null
hypothesis of independence, i.e.,
) is computed as
the sum of the cell contributions to chi-squared. It has
(r - 1) (c - 1) degrees of freedom and tests the null
hypothesis of independence, i.e.,
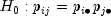 . The null
hypothesis is rejected if the computed value of
. The null
hypothesis is rejected if the computed value of 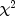 is too large.
is too large.The maximum likelihood equivalent of
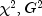 is computed as follows:
is computed as follows: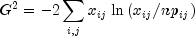
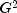 is asymptotically equivalent to
is asymptotically equivalent to
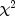 and tests the same hypothesis with the same
degrees of freedom.
and tests the same hypothesis with the same
degrees of freedom.Measures Related to Chi-squared (Phi, Contingency Coefficient, and Cramer's V)
There are three measures related to chi-squared that do not depend on sample size:
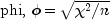
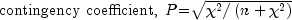
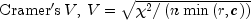
Since these statistics do not depend on sample size and are large when the hypothesis of independence is rejected, they can be thought of as measures of association and can be compared across tables with different sized samples. While both P and V have a range between 0.0 and 1.0, the upper bound of P is actually somewhat less than 1.0 for any given table (see Kendall and Stuart 1979, p. 587). The significance of all three statistics is the same as that of the
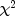 statistic, return value from the
statistic, return value from the getChiSquaredmethod.The distribution of the
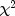 statistic in finite
samples approximates a chi-squared distribution. To compute the exact mean
and standard deviation of the
statistic in finite
samples approximates a chi-squared distribution. To compute the exact mean
and standard deviation of the 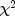 statistic,
Haldane (1939) uses the multinomial distribution with fixed table marginals.
The exact mean and standard deviation generally differ little from the mean
and standard deviation of the associated chi-squared distribution.
statistic,
Haldane (1939) uses the multinomial distribution with fixed table marginals.
The exact mean and standard deviation generally differ little from the mean
and standard deviation of the associated chi-squared distribution.Standard Errors and p-values for Some Measures of Association
In Columns 1 through 4 of statistics, estimated standard errors and asymptotic p-values are reported. Estimates of the standard errors are computed in two ways. The first estimate, in Column 1 of the return matrix from the
getStatisticsmethod, is asymptotically valid for any value of the statistic. The second estimate, in Column 2 of the array, is only correct under the null hypothesis of no association. The z-scores in Column 3 of statistics are computed using this second estimate of the standard errors. The p-values in Column 4 are computed from this z-score. See Brown and Benedetti (1977) for a discussion and formulas for the standard errors in Column 2.Measures of Association for Ranked Rows and Columns
The measures of association,
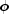 , P, and
V, do not require any ordering of the row and column categories.
Class
, P, and
V, do not require any ordering of the row and column categories.
Class ContingencyTablealso computes several measures of association for tables in which the rows and column categories correspond to ranked observations. Two of these tests, the product-moment correlation and the Spearman correlation, are correlation coefficients computed using assigned scores for the row and column categories. The cell indices are used for the product-moment correlation, while the average of the tied ranks of the row and column marginals is used for the Spearman rank correlation. Other scores are possible.Gamma, Kendall's
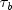 , Stuart's
, Stuart's
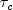 , and Somers' D are measures of
association that are computed like a correlation coefficient in the
numerator. In all these measures, the numerator is computed as the
"covariance" between the
, and Somers' D are measures of
association that are computed like a correlation coefficient in the
numerator. In all these measures, the numerator is computed as the
"covariance" between the  variables and
variables and
 variables defined above, i.e., as follows:
variables defined above, i.e., as follows: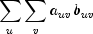
Recall that
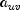 and
and 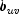 can take values -1, 0, or 1. Since the product
can take values -1, 0, or 1. Since the product
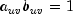 only if
only if 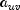 and
and
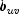 are both 1 or are both -1, it is easy to show that
this "covariance" is twice the total number of agreements minus the number
of disagreements, where a disagreement occurs when
are both 1 or are both -1, it is easy to show that
this "covariance" is twice the total number of agreements minus the number
of disagreements, where a disagreement occurs when
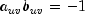 .
.Kendall's
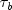 is computed as the correlation
between the
is computed as the correlation
between the 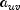 variables and the
variables and the
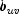 variables (see Kendall and Stuart 1979, p. 593).
In a rectangular table
variables (see Kendall and Stuart 1979, p. 593).
In a rectangular table 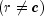 , Kendall's
, Kendall's
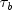 cannot be 1.0 (if all marginal totals are
positive). For this reason, Stuart suggested a modification to the
denominator of
cannot be 1.0 (if all marginal totals are
positive). For this reason, Stuart suggested a modification to the
denominator of  in which the denominator becomes
the largest possible value of the "covariance." This maximizing value is
approximately
in which the denominator becomes
the largest possible value of the "covariance." This maximizing value is
approximately 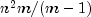 , where
m = min (r, c). Stuart's
, where
m = min (r, c). Stuart's 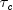 uses this approximate value in its denominator. For large
uses this approximate value in its denominator. For large
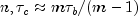 .
.Gamma can be motivated in a slightly different manner. Because the "covariance" of the
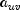 variables and the
variables and the
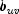 variables can be thought of as twice the number
of agreements minus the disagreements, 2(A - D), where
A is the number of agreements and D is the number of
disagreements, Gamma is motivated as the probability of agreement minus the
probability of disagreement, given that either agreement or disagreement
occurred. This is shown as
variables can be thought of as twice the number
of agreements minus the disagreements, 2(A - D), where
A is the number of agreements and D is the number of
disagreements, Gamma is motivated as the probability of agreement minus the
probability of disagreement, given that either agreement or disagreement
occurred. This is shown as 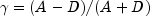 .
.Two definitions of Somers' D are possible, one for rows and a second for columns. Somers' D for rows can be thought of as the regression coefficient for predicting
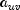 from
from
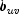 . Moreover, Somer's D for rows is the
probability of agreement minus the probability of disagreement, given that
the column variable,
. Moreover, Somer's D for rows is the
probability of agreement minus the probability of disagreement, given that
the column variable, 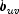 , is not 0. Somers' D
for columns is defined in a similar manner.
, is not 0. Somers' D
for columns is defined in a similar manner.A discussion of all of the measures of association in this section can be found in Kendall and Stuart (1979, p. 592).
Measures of Prediction and Uncertainty
Optimal Prediction Coefficients: The measures in this section do not require any ordering of the row or column variables. They are based entirely upon probabilities. Most are discussed in Bishop et al. (1975, p. 385).
Consider predicting (or classifying) the column for a given row in the table. Under the null hypothesis of independence, choose the column with the highest column marginal probability for all rows. In this case, the probability of misclassification for any row is 1 minus this marginal probability. If independence is not assumed within each row, choose the column with the highest row conditional probability. The probability of misclassification for the row becomes 1 minus this conditional probability.
Define the optimal prediction coefficient
 for predicting columns from
rows as the proportion of the probability of misclassification that is
eliminated because the random variables are not independent. It is
estimated by
for predicting columns from
rows as the proportion of the probability of misclassification that is
eliminated because the random variables are not independent. It is
estimated by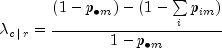
where m is the index of the maximum estimated probability in the row
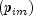 or row margin
or row margin
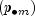 . A similar coefficient is defined for
predicting the rows from the columns. The symmetric version of the optimal
prediction
. A similar coefficient is defined for
predicting the rows from the columns. The symmetric version of the optimal
prediction 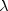 is obtained by summing the
numerators and denominators of
is obtained by summing the
numerators and denominators of  and
and
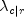 then dividing. Standard errors for
these coefficients are given in Bishop et al. (1975, p. 388).
then dividing. Standard errors for
these coefficients are given in Bishop et al. (1975, p. 388).A problem with the optimal prediction coefficients
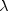 is that they vary with the marginal
probabilities. One way to correct this is to use row conditional
probabilities. The optimal prediction
is that they vary with the marginal
probabilities. One way to correct this is to use row conditional
probabilities. The optimal prediction 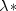 coefficients are defined as the corresponding
coefficients are defined as the corresponding 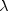 coefficients in which first the row (or column) marginals are adjusted to
the same number of observations. This yields
coefficients in which first the row (or column) marginals are adjusted to
the same number of observations. This yields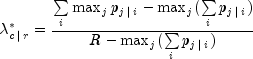
where i indexes the rows, j indexes the columns, and
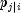 is the (estimated) probability of column
j given row i.
is the (estimated) probability of column
j given row i.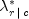
is similarly defined.
Goodman and Kruskal
 : A second kind of
prediction measure attempts to explain the proportion of the explained
variation of the row (column) measure given the column (row) measure. Define
the total variation in the rows as follows:
: A second kind of
prediction measure attempts to explain the proportion of the explained
variation of the row (column) measure given the column (row) measure. Define
the total variation in the rows as follows: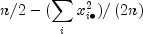
Note that this is 1/(2n) times the sums of squares of the
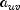 variables.
variables.With this definition of variation, the Goodman and Kruskal
 coefficient for rows is computed as the reduction
of the total variation for rows accounted for by the columns, divided by the
total variation for the rows. To compute the reduction in the total
variation of the rows accounted for by the columns, note that the total
variation for the rows within column j is defined as follows:
coefficient for rows is computed as the reduction
of the total variation for rows accounted for by the columns, divided by the
total variation for the rows. To compute the reduction in the total
variation of the rows accounted for by the columns, note that the total
variation for the rows within column j is defined as follows: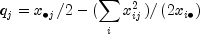
The total variation for rows within columns is the sum of the
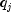 variables. Consistent with the usual methods in the
analysis of variance, the reduction in the total variation is given as the
difference between the total variation for rows and the total variation for
rows within the columns.
variables. Consistent with the usual methods in the
analysis of variance, the reduction in the total variation is given as the
difference between the total variation for rows and the total variation for
rows within the columns.Goodman and Kruskal's
 for columns is similarly
defined. See Bishop et al. (1975, p. 391) for the standard errors.
for columns is similarly
defined. See Bishop et al. (1975, p. 391) for the standard errors.Uncertainty Coefficients: The uncertainty coefficient for rows is the increase in the log-likelihood that is achieved by the most general model over the independence model, divided by the marginal log-likelihood for the rows. This is given by the following equation:
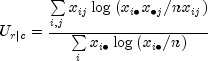
The uncertainty coefficient for columns is similarly defined. The symmetric uncertainty coefficient contains the same numerator as
 and
and 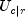 but averages
the denominators of these two statistics. Standard errors for U are
given in Brown (1983).
but averages
the denominators of these two statistics. Standard errors for U are
given in Brown (1983).Kruskal-Wallis: The Kruskal-Wallis statistic for rows is a one-way analysis-of-variance-type test that assumes the column variable is monotonically ordered. It tests the null hypothesis that no row populations are identical, using average ranks for the column variable. The Kruskal-Wallis statistic for columns is similarly defined. Conover (1980) discusses the Kruskal-Wallis test.
Test for Linear Trend: When there are two rows, it is possible to test for a linear trend in the row probabilities if it is assumed that the column variable is monotonically ordered. In this test, the probabilities for row 1 are predicted by the column index using weighted simple linear regression. This slope is given by
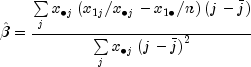
where

is the average column index. An asymptotic test that the slope is 0 may then be obtained (in large samples) as the usual regression test of zero slope.
In two-column data, a similar test for a linear trend in the column probabilities is computed. This test assumes that the rows are monotonically ordered.
Kappa: Kappa is a measure of agreement computed on square tables only. In the kappa statistic, the rows and columns correspond to the responses of two judges. The judges agree along the diagonal and disagree off the diagonal. Let
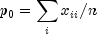
denote the probability that the two judges agree, and let
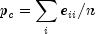
denote the expected probability of agreement under the independence model. Kappa is then given by
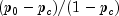 .
.McNemar Tests: The McNemar test is a test of symmetry in a square contingency table. In other words, it is a test of the null hypothesis
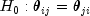 . The multiple
degrees-of-freedom version of the McNemar test with
r (r - 1)/2 degrees of freedom is computed as follows:
. The multiple
degrees-of-freedom version of the McNemar test with
r (r - 1)/2 degrees of freedom is computed as follows: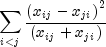
The single degree-of-freedom test assumes that the differences,
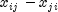 , are all in one direction. The single
degree-of-freedom test will be more powerful than the multiple
degrees-of-freedom test when this is the case. The test statistic is given
as follows:
, are all in one direction. The single
degree-of-freedom test will be more powerful than the multiple
degrees-of-freedom test when this is the case. The test statistic is given
as follows: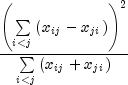
The exact probability can be computed by the binomial distribution.
- See Also:
- Example 1, Example 2, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description ContingencyTable(double[][] table)Constructs and performs a chi-squared analysis of a two-way contingency table.
-
Method Summary
Methods Modifier and Type Method and Description doublegetChiSquared()Returns the Pearson chi-squared test statistic.doublegetContingencyCoef()Returns contingency coefficient.double[][]getContributions()Returns the contributions to chi-squared for each cell in the table.doublegetCramersV()Returns Cramer's V.intgetDegreesOfFreedom()Returns the degrees of freedom for the chi-squared tests associated with the table.doublegetExactMean()Returns exact mean.doublegetExactStdev()Returns exact standard deviation.double[][]getExpectedValues()Returns the expected values of each cell in the table.doublegetGSquared()Returns the likelihood ratio G2 (chi-squared).doublegetGSquaredP()Returns the probability of a larger G2 (chi-squared).doublegetP()Returns the Pearson chi-squared p-value for independence of rows and columns.doublegetPhi()Returns phi.double[][]getStatistics()Returns the statistics associated with this table.
-
-
-
Constructor Detail
-
ContingencyTable
public ContingencyTable(double[][] table)
Constructs and performs a chi-squared analysis of a two-way contingency table.- Parameters:
table- Adoublematrix containing the observed counts in the contingency table.
-
-
Method Detail
-
getChiSquared
public double getChiSquared()
Returns the Pearson chi-squared test statistic.- Returns:
- A
doublescalar containing the Pearson chi-squared test statistic.
-
getContingencyCoef
public double getContingencyCoef()
Returns contingency coefficient.- Returns:
- A
doublescalar containing the contingency coefficient based on Pearson chi-squared statistic.
-
getContributions
public double[][] getContributions()
Returns the contributions to chi-squared for each cell in the table.- Returns:
- A
doublematrix of size (table.length+1) * (table[0].length+1) containing the contributions to chi-squared for each cell in the table. The last row and column contain the total contribution to chi-squared for that row or column.
-
getCramersV
public double getCramersV()
Returns Cramer's V.- Returns:
- A
doublescalar containing the Cramer's V based on Pearson chi-squared statistic.
-
getDegreesOfFreedom
public int getDegreesOfFreedom()
Returns the degrees of freedom for the chi-squared tests associated with the table.- Returns:
- An
intscalar containing the degrees of freedom for the chi-squared tests associated with the table.
-
getExactMean
public double getExactMean()
Returns exact mean.- Returns:
- A
doublescalar containing the exact mean based on Pearson's chi-square statistic.
-
getExactStdev
public double getExactStdev()
Returns exact standard deviation.- Returns:
- A
doublescalar containing the exact standard deviation based on Pearson's chi-square statistic.
-
getExpectedValues
public double[][] getExpectedValues()
Returns the expected values of each cell in the table.- Returns:
- A
doublematrix of size (table.length+1) * (table[0].length+1) containing the expected values of each cell in the table, under the null hypothesis. The marginal totals are in the last row and column.
-
getGSquared
public double getGSquared()
Returns the likelihood ratio G2 (chi-squared).- Returns:
- A
doublescalar containing the likelihood ratio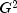 (chi-squared).
(chi-squared).
-
getGSquaredP
public double getGSquaredP()
Returns the probability of a larger G2 (chi-squared).- Returns:
- A
doublescalar containing the probability of a larger (chi-squared).
(chi-squared).
-
getP
public double getP()
Returns the Pearson chi-squared p-value for independence of rows and columns.- Returns:
- A
doublescalar containing the Pearson chi-squared p-value for independence of rows and columns.
-
getPhi
public double getPhi()
Returns phi.- Returns:
- A
doublescalar containing the phi based on Pearson chi-squared statistic.
-
getStatistics
public double[][] getStatistics()
Returns the statistics associated with this table.- Returns:
- A
doublematrix of size 23 * 5 containing statistics associated with this table. Each row corresponds to a statistic.Row Statistics 0 gamma 1 Kendall's 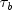
2 Stuart's 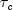
3 Somers' D for rows (given columns) 4 Somers' D for columns (given rows) 5 product moment correlation 6 Spearman rank correlation 7 Goodman and Kruskal  for rows (given
columns)
for rows (given
columns)8 Goodman and Kruskal  for columns (given
rows)
for columns (given
rows)9 uncertainty coefficient U (symmetric) 10 uncertainty 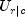 (rows)
(rows)11 uncertainty 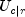 (columns)
(columns)12 optimal prediction 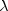 (symmetric)
(symmetric)13 optimal prediction 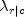 (rows)
(rows)14 optimal prediction  (columns)
(columns)15 optimal prediction 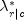 (rows)
(rows)16 optimal prediction  (columns)
(columns)17 test for linear trend in row probabilities if table.length= 2. Iftable.lengthis not 2, a test for linear trend in column probabilities if table[0].length = 2.18 Kruskal-Wallis test for no row effect 19 Kruskal-Wallis test for no column effect 20 kappa (square tables only) 21 McNemar test of symmetry (square tables only) 22 McNemar one degree of freedom test of symmetry (square tables only) If a statistic cannot be computed, or if some value is not relevant for the computed statistic, the entry is NaN (Not a Number).
The columns are as follows:
In the McNemar tests, column 0 contains the statistic, column 1 contains the chi-squared degrees of freedom, column 3 contains the exact p-value (1 degree of freedom only), and column 4 contains the chi-squared asymptotic p-value. The Kruskal-Wallis test is the same except no exact p-value is computed.Column Value 0 estimated statistic 1 standard error for any parameter value 2 standard error under the null hypothesis 3 t value for testing the null hypothesis 4 p-value of the test in column 3
-
-