- java.lang.Object
-
- com.imsl.stat.CrossCorrelation
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class CrossCorrelation extends Object implements Serializable, Cloneable
Computes the sample cross-correlation function of two stationary time series.CrossCorrelationestimates the cross-correlation function of two jointly stationary time series given a sample of n =x.lengthobservations and
and 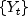 for t = 1,2, ..., n.
for t = 1,2, ..., n.Let
be the estimate of the mean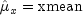
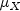 of the time series
of the time series
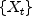 where
where 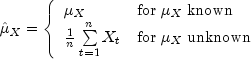
The autocovariance function of
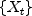 ,
,
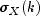 , is estimated by
, is estimated by
where K =
maximum_lag. Note that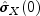 is
equivalent to the sample variance of
is
equivalent to the sample variance of xreturned by methodgetVarianceX. The autocorrelation function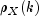 is estimated by
is estimated by
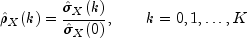
Note that
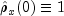 by definition.
Let
by definition.
Let
be similarly defined.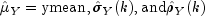
The cross-covariance function
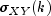 is
estimated by
is
estimated by
The cross-correlation function
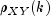 is
estimated by
is
estimated by ![hat rho _{XY}(k) =
frac{hat sigma _{XY}(k)} {[hatsigma _X(0) hatsigma _Y(0) ]^{frac{1}{2}}}
;;; {k = 0,pm1, dots,pm K}](eqn_3305.png)
The standard errors of the sample cross-correlations may be optionally computed according to the getStandardErrors method argument
stderrMethod. One method is based on a general asymptotic expression for the variance of the sample cross-correlation coefficient of two jointly stationary time series with independent, identically distributed normal errors given by Bartlet (1978, page 352). The theoretical formula is
For computational purposes, the autocorrelations![begin{array}{c}
{rm var} left { hat rho _{XY}(k) right } =
frac{1}{n-k}sumlimits_{i=-infty}^{infty}
left [right. {rho _X(i)}+rho _{XY}(i-k)rho _{XY}(i+k) \
-2rho _{XY}(k){rho _X(i)rho _{XY}(i+k)+rho _{XY}(-i)rho _Y(i+k)} \
+rho^2_{XY}(k){rho_X(i) + frac{1}{2}rho^2_X(i) +
frac{1}{2}rho^2_Y(i)} left. right ] end{array}](eqn_3306.png)
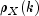 and
and 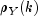 and the cross-correlations
and the cross-correlations 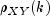 are replaced by their corresponding estimates for
are replaced by their corresponding estimates for
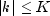 ,
and the limits of summation are equal to zero for all k such that
,
and the limits of summation are equal to zero for all k such that
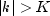 .
.
A second method evaluates Bartlett's formula under the additional assumption that the two series have no cross-correlation. The theoretical formula is
For additional special cases of Bartlett's formula, see Box and Jenkins (1976, page 377).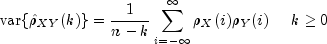
An important property of the cross-covariance coefficient is
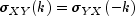 for
for
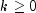 . This result is used in the computation
of the standard error of the sample cross-correlation for lag
. This result is used in the computation
of the standard error of the sample cross-correlation for lag 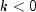 .
In general, the cross-covariance function is not symmetric about zero
so both positive and negative lags are of interest.
.
In general, the cross-covariance function is not symmetric about zero
so both positive and negative lags are of interest.- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classCrossCorrelation.NonPosVariancesExceptionThe problem is ill-conditioned.
-
Field Summary
Fields Modifier and Type Field and Description static intBARTLETTS_FORMULAIndicates standard error computation using Bartlett's formula.static intBARTLETTS_FORMULA_NOCCIndicates standard error computation using Bartlett's formula with the assumption of no cross-correlation.
-
Constructor Summary
Constructors Constructor and Description CrossCorrelation(double[] x, double[] y, int maximum_lag)Constructor to compute the sample cross-correlation function of two stationary time series.
-
Method Summary
Methods Modifier and Type Method and Description double[]getAutoCorrelationX()Returns the autocorrelations of the time seriesx.double[]getAutoCorrelationY()Returns the autocorrelations of the time seriesy.double[]getAutoCovarianceX()Returns the autocovariances of the time seriesx.double[]getAutoCovarianceY()Returns the autocovariances of the time seriesy.double[]getCrossCorrelation()Returns the cross-correlations between the time seriesxandy.double[]getCrossCovariance()Returns the cross-covariances between the time seriesxandy.doublegetMeanX()Returns the mean of the time seriesx.doublegetMeanY()Returns the mean of the time seriesy.double[]getStandardErrors(int stderrMethod)Returns the standard errors of the cross-correlations between the time seriesxandy.doublegetVarianceX()Returns the variance of time seriesx.doublegetVarianceY()Returns the variance of time seriesy.voidsetMeanX(double mean)Estimate of the mean of time seriesx.voidsetMeanY(double mean)Estimate of the mean of time seriesy.
-
-
-
Field Detail
-
BARTLETTS_FORMULA
public static final int BARTLETTS_FORMULA
Indicates standard error computation using Bartlett's formula.- See Also:
- Constant Field Values
-
BARTLETTS_FORMULA_NOCC
public static final int BARTLETTS_FORMULA_NOCC
Indicates standard error computation using Bartlett's formula with the assumption of no cross-correlation.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
CrossCorrelation
public CrossCorrelation(double[] x, double[] y, int maximum_lag)Constructor to compute the sample cross-correlation function of two stationary time series.- Parameters:
x- A one-dimensionaldoublearray containing the first stationary time series.y- A one-dimensionaldoublearray containing the second stationary time series.maximum_lag- Anintcontaining the maximum lag of the cross-covariance and cross-correlations to be computed.maximum_lagmust be greater than or equal to 1 and less than the minimum of the number of observations ofxandy.
-
-
Method Detail
-
getAutoCorrelationX
public double[] getAutoCorrelationX() throws CrossCorrelation.NonPosVariancesExceptionReturns the autocorrelations of the time seriesx.- Returns:
- A
doublearray of lengthmaximum_lag+1 containing the autocorrelations of the time seriesx. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag k where k = 1, ...,maximum_lag. - Throws:
CrossCorrelation.NonPosVariancesException
-
getAutoCorrelationY
public double[] getAutoCorrelationY() throws CrossCorrelation.NonPosVariancesExceptionReturns the autocorrelations of the time seriesy.- Returns:
- A
doublearray of lengthmaximum_lag+1 containing the autocorrelations of the time seriesy. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag k where k = 1, ...,maximum_lag. - Throws:
CrossCorrelation.NonPosVariancesException
-
getAutoCovarianceX
public double[] getAutoCovarianceX() throws CrossCorrelation.NonPosVariancesExceptionReturns the autocovariances of the time seriesx.- Returns:
- A
doublearray of lengthmaximum_lag+1 containing the variances and autocovariances of the time seriesx. The 0-th element of the array contains the variance of the time seriesx. The k-th element contains the autocovariance of lag k where k = 1, ...,maximum_lag. - Throws:
CrossCorrelation.NonPosVariancesException
-
getAutoCovarianceY
public double[] getAutoCovarianceY() throws CrossCorrelation.NonPosVariancesExceptionReturns the autocovariances of the time seriesy.- Returns:
- A
doublearray of lengthmaximum_lag+1 containing the variances and autocovariances of the time seriesy. The 0-th element of the array contains the variance of the time seriesx. The k-th element contains the autocovariance of lag k where k = 1, ...,maximum_lag. - Throws:
CrossCorrelation.NonPosVariancesException
-
getCrossCorrelation
public double[] getCrossCorrelation() throws CrossCorrelation.NonPosVariancesExceptionReturns the cross-correlations between the time seriesxandy.- Returns:
- A
doublearray of length 2 *maximum_lag+1 containing the cross-correlations between the time seriesxandy. The cross-correlation betweenxandyat lag k, where k = -maximum_lag,..., 0, 1,...,maximum_lag, corresponds to output array indices0, 1,..., (2*maximum_lag). - Throws:
CrossCorrelation.NonPosVariancesException
-
getCrossCovariance
public double[] getCrossCovariance()
Returns the cross-covariances between the time seriesxandy.- Returns:
- A
doublearray of length 2 *maximum_lag+1 containing the cross-covariances between the time seriesxandy. The cross-covariance betweenxandyat lag k, where k = -maximum_lag,..., 0, 1,...,maximum_lag, corresponds to output array indices0, 1,..., (2*maximum_lag).
-
getMeanX
public double getMeanX()
Returns the mean of the time seriesx.- Returns:
- A
doublecontaining the mean of the time seriesx.
-
getMeanY
public double getMeanY()
Returns the mean of the time seriesy.- Returns:
- A
doublecontaining the mean of the time seriesy.
-
getStandardErrors
public double[] getStandardErrors(int stderrMethod) throws CrossCorrelation.NonPosVariancesExceptionReturns the standard errors of the cross-correlations between the time seriesxandy. Method of computation for standard errors of the cross-correlation is determined by thestderrMethodparameter. IfstderrMethodis set to BARTLETTS_FORMULA, Bartlett's formula is used to compute the standard errors of cross-correlations. IfstderrMethodis set to BARTLETTS_FORMULA_NOCC, Bartlett's formula is used to compute the standard errors of cross-correlations, with the assumption of no cross-correlation.- Parameters:
stderrMethod- Anintspecifying the method to compute the standard errors of cross-correlations between the time seriesxandy.- Returns:
- A
doublearray of length 2 *maximum_lag+ 1 containing the standard errors of the cross-correlations between the time seriesxandy. The standard error of cross-correlations betweenxandyat lag k, where k = -maximum_lag,..., 0, 1,...,maximum_lag, corresponds to output array indices 0, 1,...,(2*maximum_lag). - Throws:
CrossCorrelation.NonPosVariancesException
-
getVarianceX
public double getVarianceX() throws CrossCorrelation.NonPosVariancesExceptionReturns the variance of time seriesx.- Returns:
- A
doublecontaining the variance of the time seriesx. - Throws:
CrossCorrelation.NonPosVariancesException
-
getVarianceY
public double getVarianceY() throws CrossCorrelation.NonPosVariancesExceptionReturns the variance of time seriesy.- Returns:
- A
doublecontaining the variance of the time seriesy. - Throws:
CrossCorrelation.NonPosVariancesException
-
setMeanX
public void setMeanX(double mean)
Estimate of the mean of time seriesx.- Parameters:
mean- Adoublecontaining the estimate mean of the time seriesx.
-
setMeanY
public void setMeanY(double mean)
Estimate of the mean of time seriesy.- Parameters:
mean- Adoublecontaining the estimate mean of the time seriesy.
-
-