- java.lang.Object
-
- com.imsl.stat.FactorAnalysis
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class FactorAnalysis extends Object implements Serializable, Cloneable
Performs Principal Component Analysis or Factor Analysis on a covariance or correlation matrix.Class
FactorAnalysiscomputes principal components or initial factor loading estimates for a variance-covariance or correlation matrix using exploratory factor analysis models.Models available are the principal component model for factor analysis and the common factor model with additions to the common factor model in alpha factor analysis and image analysis. Methods of estimation include principal components, principal factor, image analysis, unweighted least squares, generalized least squares, and maximum likelihood.
For the principal component model there are methods to compute the characteristic roots, characteristic vectors, standard errors for the characteristic roots, and the correlations of the principal component scores with the original variables. Principal components obtained from correlation matrices are the same as principal components obtained from standardized (to unit variance) variables.
The principal component scores are the elements of the vector
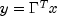 where
where 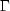 is the matrix whose columns are the characteristic
vectors (eigenvectors) of the sample covariance (or correlation) matrix and x
is the vector of observed (or standardized) random variables. The variances of the
principal component scores are the characteristic roots (eigenvalues) of the
covariance (correlation) matrix.
is the matrix whose columns are the characteristic
vectors (eigenvectors) of the sample covariance (or correlation) matrix and x
is the vector of observed (or standardized) random variables. The variances of the
principal component scores are the characteristic roots (eigenvalues) of the
covariance (correlation) matrix.Asymptotic variances for the characteristic roots were first obtained by Girshick (1939) and are given more recently by Kendall, Stuart, and Ord (1983, page 331). These variances are computed either for variance-covariance matrices or for correlation matrices.
The correlations of the principal components with the observed (or standardized) variables are the same as the unrotated factor loadings obtained for the principal components model for factor analysis when a correlation matrix is input.
In the factor analysis model used for factor extraction, the basic model is given as
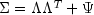 where
where 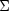 is the
is the 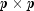 population covariance matrix.
population covariance matrix. 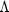 is the
is the 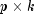 matrix of factor loadings relating the factors
f to the observed variables x, and
matrix of factor loadings relating the factors
f to the observed variables x, and 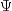 is the
is the  matrix of covariances of the unique errors e.
Here, p represents the number of variables and k is the
number of factors. The relationship between the factors, the unique errors, and the
observed variables is given as
matrix of covariances of the unique errors e.
Here, p represents the number of variables and k is the
number of factors. The relationship between the factors, the unique errors, and the
observed variables is given as 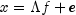 where, in addition,
it is assumed that the expected values of e, f, and
x are zero. (The sample means can be subtracted from x if
the expected value of x is not zero.) It is also assumed that each factor
has unit variance, the factors are independent of each other, and that the factors and the
unique errors are mutually independent. In the common factor model, the elements of the
vector of unique errors e are also assumed to be independent of one
another so that the matrix
where, in addition,
it is assumed that the expected values of e, f, and
x are zero. (The sample means can be subtracted from x if
the expected value of x is not zero.) It is also assumed that each factor
has unit variance, the factors are independent of each other, and that the factors and the
unique errors are mutually independent. In the common factor model, the elements of the
vector of unique errors e are also assumed to be independent of one
another so that the matrix 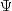 is diagonal. This is not the case
in the principal component model in which the errors may be correlated.
is diagonal. This is not the case
in the principal component model in which the errors may be correlated. Further differences between the various methods concern the criterion that is optimized and the amount of computer effort required to obtain estimates. Generally speaking, the least-squares and maximum likelihood methods, which use iterative algorithms, require the most computer time with the principal factor, principal component, and the image methods requiring much less time since the algorithms in these methods are not iterative. The algorithm in alpha factor analysis is also iterative, but the estimates in this method generally require somewhat less computer effort than the least-squares and maximum likelihood estimates. In all algorithms one eigensystem analysis is required on each iteration.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classFactorAnalysis.BadVarianceExceptionBad variance error.static classFactorAnalysis.EigenvalueExceptionEigenvalue error.static classFactorAnalysis.NonPositiveEigenvalueExceptionNon positive eigenvalue error.static classFactorAnalysis.NotPositiveSemiDefiniteExceptionCovariance matrix not positive semi-definite.static classFactorAnalysis.NotSemiDefiniteExceptionHessian matrix not semi-definite.static classFactorAnalysis.RankExceptionRank of covariance matrix error.static classFactorAnalysis.SingularExceptionCovariance matrix singular error.
-
Field Summary
Fields Modifier and Type Field and Description static intALPHA_FACTOR_ANALYSISIndicates alpha factor analysis.static intCORRELATION_MATRIXIndicates correlation matrix.static intGENERALIZED_LEAST_SQUARESIndicates generalized least squares method.static intIMAGE_FACTOR_ANALYSISIndicates image factor analysis.static intMAXIMUM_LIKELIHOODIndicates maximum likelihood method.static intPRINCIPAL_COMPONENT_MODELIndicates principal component model.static intPRINCIPAL_FACTOR_MODELIndicates principal factor model.static intUNWEIGHTED_LEAST_SQUARESIndicates unweighted least squares method.static intVARIANCE_COVARIANCE_MATRIXIndicates variance-covariance matrix.
-
Constructor Summary
Constructors Constructor and Description FactorAnalysis(double[][] cov, int matrixType, int nf)Constructor forFactorAnalysis.
-
Method Summary
Methods Modifier and Type Method and Description double[][]getCorrelations()Returns the correlations of the principal components.double[][]getFactorLoadings()Returns the unrotated factor loadings.double[]getParameterUpdates()Returns the parameter updates.double[]getPercents()Returns the cumulative percent of the total variance explained by each principal component.double[]getStandardErrors()Returns the estimated asymptotic standard errors of the eigenvalues.double[]getStatistics()Returns statistics.double[]getValues()Returns the eigenvalues.double[]getVariances()Gets the unique variances.double[][]getVectors()Returns the eigenvectors.voidsetConvergenceCriterion1(double eps)Sets the convergence criterion used to terminate the iterations.voidsetConvergenceCriterion2(double epse)Sets the convergence criterion used to switch to exact second derivatives.voidsetDegreesOfFreedom(int ndf)Sets the number of degrees of freedom.voidsetFactorLoadingEstimationMethod(int methodType)Sets the factor loading estimation method.voidsetMaxIterations(int maxit)Sets the maximum number of iterations in the iterative procedure.voidsetMaxStep(int maxstp)Sets the maximum number of step halvings allowed during an iteration.voidsetVarianceEstimationMethod(int init)Sets the variance estimation method.voidsetVariances(double[] uniq)Sets the variances.
-
-
-
Field Detail
-
ALPHA_FACTOR_ANALYSIS
public static final int ALPHA_FACTOR_ANALYSIS
Indicates alpha factor analysis.- See Also:
- Constant Field Values
-
CORRELATION_MATRIX
public static final int CORRELATION_MATRIX
Indicates correlation matrix.- See Also:
- Constant Field Values
-
GENERALIZED_LEAST_SQUARES
public static final int GENERALIZED_LEAST_SQUARES
Indicates generalized least squares method.- See Also:
- Constant Field Values
-
IMAGE_FACTOR_ANALYSIS
public static final int IMAGE_FACTOR_ANALYSIS
Indicates image factor analysis.- See Also:
- Constant Field Values
-
MAXIMUM_LIKELIHOOD
public static final int MAXIMUM_LIKELIHOOD
Indicates maximum likelihood method.- See Also:
- Constant Field Values
-
PRINCIPAL_COMPONENT_MODEL
public static final int PRINCIPAL_COMPONENT_MODEL
Indicates principal component model.- See Also:
- Constant Field Values
-
PRINCIPAL_FACTOR_MODEL
public static final int PRINCIPAL_FACTOR_MODEL
Indicates principal factor model.- See Also:
- Constant Field Values
-
UNWEIGHTED_LEAST_SQUARES
public static final int UNWEIGHTED_LEAST_SQUARES
Indicates unweighted least squares method.- See Also:
- Constant Field Values
-
VARIANCE_COVARIANCE_MATRIX
public static final int VARIANCE_COVARIANCE_MATRIX
Indicates variance-covariance matrix.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
FactorAnalysis
public FactorAnalysis(double[][] cov, int matrixType, int nf)Constructor forFactorAnalysis.- Parameters:
cov- Adoublematrix containing the covariance or correlation matrix.matrixType- Anintscalar indicating the type of matrix that is input. Uses class memberVARIANCE_COVARIANCE_MATRIX,CORRELATION_MATRIXformatrixType.nf- Anintscalar indicating the number of factors in the model. Ifnfis not known in advance, several different values ofnfshould be used, and the most reasonable value kept in the final solution. Since, in practice, the non-iterative methods often lead to solutions which differ little from the iterative methods, it is usually suggested that a non-iterative method be used in the initial stages of the factor analysis, and that the iterative methods be used once issues such as the number of factors have been resolved.- Throws:
IllegalArgumentException- is thrown ifx.length, andx[0].lengthare equal to 0.
-
-
Method Detail
-
getCorrelations
public double[][] getCorrelations() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the correlations of the principal components.- Returns:
- An
doublematrix containing the correlations of the principal components with the observed/standardized variables. If a covariance matrix is input to the constructor, then the correlations are with the observed variables. Otherwise, the correlations are with the standardized (to a variance of 1.0) variables. Only valid for the principal components model. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getFactorLoadings
public double[][] getFactorLoadings() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the unrotated factor loadings.- Returns:
- A
doublematrix containing the unrotated factor loadings. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getParameterUpdates
public double[] getParameterUpdates() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the parameter updates.- Returns:
- A
doublearray containing the parameter updates when convergence was reached (or the iterations terminated). The parameter updates are only meaningful for the common factor model. The parameter updates are set to 0.0 for the principal component model. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getPercents
public double[] getPercents() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the cumulative percent of the total variance explained by each principal component. Valid for the principal component model.- Returns:
- An
doublearray containing the total variance explained by each principal component. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getStandardErrors
public double[] getStandardErrors() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the estimated asymptotic standard errors of the eigenvalues.- Returns:
- An
doublearray containing the estimated asymptotic standard errors of the eigenvalues. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getStatistics
public double[] getStatistics() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns statistics.- Returns:
- A
doublearray (Stat) containing output statistics. Stat is not defined and is set to NaN when the method used to obtain the estimates, is the principal component method, principal factor method, image factor analysis method, or alpha analysis method.i Stat[i] 0 Value of the function minimum. 1 Tucker reliability coefficient. 2 Chi-squared test statistic for testing that the number of factors in the model are adequate for the data. 3 Degrees of freedom in chi-squared. This is computed as
where
nvaris the number of variables andnfis the number of factors in the model.4 Probability of a greater chi-squared statistic. 5 Number of iterations. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getValues
public double[] getValues() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the eigenvalues.- Returns:
- A
doublearray containing the eigenvalues of the matrix from which the factors were extracted ordered from largest to smallest. If Alpha Factor analysis is used, then the firstnfpositions of the array contain the Alpha coefficients. Here,nfis the number of factors in the model. If the algorithm fails to converge for a particular eigenvalue, that eigenvalue is set to NaN. Note that the eigenvalues are usually not the eigenvalues of the input matrix cov. They are the eigenvalues of the input matrix cov when theprincipal componentmethod is used. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getVariances
public double[] getVariances() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionGets the unique variances.- Returns:
- A
doublearray of length nvar containing the unique variances, wherenvaris the number of variables. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
getVectors
public double[][] getVectors() throws FactorAnalysis.RankException, FactorAnalysis.NotSemiDefiniteException, FactorAnalysis.NotPositiveSemiDefiniteException, FactorAnalysis.SingularException, FactorAnalysis.BadVarianceException, FactorAnalysis.EigenvalueException, FactorAnalysis.NonPositiveEigenvalueExceptionReturns the eigenvectors.- Returns:
- A
doublematrix containing the eigenvectors of the matrix from which the factors were extracted. The j-th column of the eigenvector matrix corresponds to the j-th eigenvalue. The eigenvectors are normalized to each have Euclidean length equal to one. Also, the sign of each vector is set so that the largest component in magnitude (the first of the largest if there are ties) is made positive. Note that the eigenvectors are usually not the eigenvectors of the input matrix cov. They are the eigenvectors of the input matrix cov when theprincipal componentmethod is used. - Throws:
FactorAnalysis.RankExceptionFactorAnalysis.NotSemiDefiniteExceptionFactorAnalysis.NotPositiveSemiDefiniteExceptionFactorAnalysis.SingularExceptionFactorAnalysis.BadVarianceExceptionFactorAnalysis.EigenvalueExceptionFactorAnalysis.NonPositiveEigenvalueException
-
setConvergenceCriterion1
public void setConvergenceCriterion1(double eps)
Sets the convergence criterion used to terminate the iterations.- Parameters:
eps- Adoubleused to terminate the iterations. For the least squares and and maximum likelihood methods convergence is assumed when the relative change in the criterion is less thaneps. For alpha factor analysis, convergence is assumed when the maximum change (relative to the variance) of a uniqueness is less thaneps.epsis not referenced for the other estimation methods. If this member function is not called,epsis set to 0.0001.
-
setConvergenceCriterion2
public void setConvergenceCriterion2(double epse)
Sets the convergence criterion used to switch to exact second derivatives.- Parameters:
epse- Adoubleused to switch to exact second derivatives. When the largest relative change in the unique standard deviation vector is less thanepseexact second derivative vectors are used. If this member function is not called,epseis set to 0.1. Not referenced for principal component, principal factor, image factor, or alpha factor methods.
-
setDegreesOfFreedom
public void setDegreesOfFreedom(int ndf)
Sets the number of degrees of freedom.- Parameters:
ndf- Anintvalue specifying the number of degrees of freedom in the input matrix. If this member function is not called 100 degrees of freedom are assumed.
-
setFactorLoadingEstimationMethod
public void setFactorLoadingEstimationMethod(int methodType)
Sets the factor loading estimation method.- Parameters:
methodType- Anintscalar indicating the method to be applied for obtaining the factor loadings. Use class memberPRINCIPAL_COMPONENT_MODEL,PRINCIPAL_FACTOR_MODEL,UNWEIGHTED_LEAST_SQUARES,GENERALIZED_LEAST_SQUARES,MAXIMUM_LIKELIHOOD,IMAGE_FACTOR_ANALYSIS, orALPHA_FACTOR_ANALYSISformethodType. If this member function is not called, thePRINCIPAL_COMPONENT_MODELis used.For the principal component and principal factor methods, the factor loading estimates are computed as
where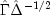
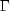 and the diagonal matrix
and the diagonal matrix  are
the eigenvalues and eigenvectors of a matrix. In the principal component model, the eigensystem
analysis is performed on the sample covariance (correlation) matrix
are
the eigenvalues and eigenvectors of a matrix. In the principal component model, the eigensystem
analysis is performed on the sample covariance (correlation) matrix 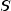 while in the principal factor model the matrix
while in the principal factor model the matrix 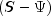 is used.
If the unique error variances
is used.
If the unique error variances 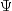 are not known in the principal factor
model, then they are estimated. This is achieved by calling the member function
are not known in the principal factor
model, then they are estimated. This is achieved by calling the member function setVarianceEstimationMethodand settinginitto 0. If the principal component model is used, the error variances are set to 0.0 automatically.The basic idea in the principal component method is to find factors that maximize the variance in the original data that is explained by the factors. Because this method allows the unique errors to be correlated, some factor analysts insist that the principal component method is not a factor analytic method. Usually however, the estimates obtained via the principal component model and other models in factor analysis will be quite similar.
It should be noted that both the principal component and the principal factor methods give different results when the correlation matrix is used in place of the covariance matrix. Indeed, any rescaling of the sample covariance matrix can lead to different estimates with either of these methods. A further difficulty with the principal factor method is the problem of estimating the unique error variances. Theoretically, these must be known in advance and passed in through member function
setVariances. In practice, the estimates of these parameters produced by calling the member functionsetVarianceEstimationMethodand settinginitto 0 are often used. In either case, the resulting adjusted covariance (correlation) matrix
may not yield the
nfpositive eigenvalues required fornffactors to be obtained. If this occurs, the user must either lower the number of factors to be estimated or give new unique error variance values.For the least-squares and maximum likelihood methods an iterative algorithm is used to obtain the estimates (see Joreskog 1977). As with the principal factor model, the user may either input the initial unique error variances or allow the algorithm to compute initial estimates. Unlike the principal factor method, the code then optimizes the criterion function with respect to both
 and
and  . (In the
principal factor method,
. (In the
principal factor method, 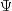 is assumed to be known. Given
is assumed to be known. Given 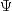 ,
estimates for
,
estimates for  may be obtained.)
may be obtained.) The major differences between the estimation methods described in this member function are in the criterion function that is optimized. Let
 denote the
sample covariance (correlation) matrix, and let
denote the
sample covariance (correlation) matrix, and let 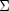 denote the
covariance matrix that is to be estimated by the factor model. In the unweighted
least-squares method, also called the iterated principal factor method or the minres
method (see Harman 1976, page 177), the function minimized is the sum of the squared
differences between
denote the
covariance matrix that is to be estimated by the factor model. In the unweighted
least-squares method, also called the iterated principal factor method or the minres
method (see Harman 1976, page 177), the function minimized is the sum of the squared
differences between  and
and 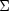 . This is
written as
. This is
written as 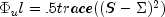 .
. Generalized least-squares and maximum likelihood estimates are asymptotically equivalent methods. Maximum likelihood estimates maximize the (normal theory) likelihood
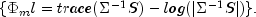 while
generalized least squares optimizes the function
while
generalized least squares optimizes the function 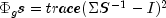 .
.In all three methods, a two-stage optimization procedure is used. This proceeds by first solving the likelihood equations for
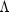 in terms of
in terms of  and substituting the solution into the likelihood. This gives a criterion
and substituting the solution into the likelihood. This gives a criterion 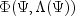 ,
which is optimized with respect to
,
which is optimized with respect to  . In the second stage, the estimates
. In the second stage, the estimates
are obtained from the estimates for
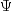 .
.
The generalized least-squares and the maximum likelihood methods allow for the computation of a statistic for testing that
nfcommon factors are adequate to fit the model. This is a chi-squared test that all remaining parameters associated with additional factors are zero. If the probability of a larger chi-squared is small (seestat[4]undergetStatistics) so that the null hypothesis is rejected, then additional factors are needed (although these factors may not be of any practical importance). Failure to reject does not legitimize the model. The statisticstat[2]is a likelihood ratio statistic in maximum likelihood estimates. As such, it asymptotically follows a chi-squared distribution with degrees of freedom given instat[3].The Tucker and Lewis (1973) reliability coefficient,
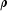 , is returned
in
, is returned
in stat[1]when the maximum likelihood or generalized least-squares methods are used. This coefficient is an estimate of the ratio of explained to the total variation in the data. It is computed as follows:
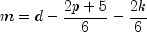
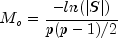
where
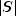 is the determinant of
is the determinant of cov, p is the number of variables, k is the number of factors,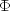 is
the optimized criterion, and d is the number of degrees of freedom.
is
the optimized criterion, and d is the number of degrees of freedom.
The term "image analysis" is used here to denote the noniterative image method of Kaiser (1963). It is not the image factor analysis discussed by Harman (1976, page 226). The image method (as well as the alpha factor analysis method) begins with the notion that only a finite number from an infinite number of possible variables have been measured. The image factor pattern is calculated under the assumption that the ratio of the number of factors to the number of observed variables is near zero so that a very good estimate for the unique error variances (for standardized variables) is given as one minus the squared multiple correlation of the variable under consideration with all variables in the covariance matrix.
First, the matrix
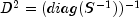 is computed where the
operator "diag" results in a matrix consisting of the diagonal elements of its argument,
and
is computed where the
operator "diag" results in a matrix consisting of the diagonal elements of its argument,
and 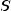 is the sample covariance (correlation) matrix. Then, the
eigenvalues
is the sample covariance (correlation) matrix. Then, the
eigenvalues 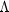 and eigenvectors
and eigenvectors 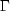 of
the matrix
of
the matrix 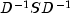 are computed. Finally, the unrotated image
factor pattern matrix is computed as
are computed. Finally, the unrotated image
factor pattern matrix is computed as ![A = DGamma[(Lambda - I)^2 Lambda^{-1}]^{1/2}](eqn_3220.png) .
. The alpha factor analysis method of Kaiser and Caffrey (1965) finds factor-loading estimates to maximize the correlation between the factors and the complete universe of variables of interest. The basic idea in this method is as follows: only a finite number of variables out of a much larger set of possible variables is observed. The population factors are linearly related to this larger set while the observed factors are linearly related to the observed variables. Let f denote the factors obtainable from a finite set of observed random variables, and let
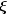 denote the factors obtainable from the universe of observable variables. Then, the
alpha method attempts to find factor-loading estimates so as to maximize the correlation
between f and
denote the factors obtainable from the universe of observable variables. Then, the
alpha method attempts to find factor-loading estimates so as to maximize the correlation
between f and  . In order to obtain these
estimates, the iterative algorithm of Kaiser and Caffrey (1965) is used.
. In order to obtain these
estimates, the iterative algorithm of Kaiser and Caffrey (1965) is used.
-
setMaxIterations
public void setMaxIterations(int maxit)
Sets the maximum number of iterations in the iterative procedure.- Parameters:
maxit- Anintused as the maximum number of iterations allowed during the iterative portion of the algorithm. If this member function is not called,maxitis set to 60. Not referenced for factor loading methods principal component, principal factor, or image factor methods.
-
setMaxStep
public void setMaxStep(int maxstp)
Sets the maximum number of step halvings allowed during an iteration.- Parameters:
maxstp- Anintused as the maximum number of step halvings allowed during an iteration. If this member function is not called,maxstpis set to 8. Not referenced for principal component, principal factor, image factor, or alpha factor methods.
-
setVarianceEstimationMethod
public void setVarianceEstimationMethod(int init)
Sets the variance estimation method.- Parameters:
init- Anintused to designate the method to be applied for obtaining the initial estimates of the unique variances. If this member function is not called,initis set to 1.
Note that when the factor loading estimation method is PRINCIPAL_COMPONENT_MODEL, the initial estimates ininit Method 0 Initial estimates are taken as the constant 1-nf/(2*nvar) divided by the diagonal elements of the inverse of input matrix cov, wherenvaris the number of variables.1 Initial estimates are input by the user in vector uniq (setVariances).uniqare reset to 0.0.
-
setVariances
public void setVariances(double[] uniq)
Sets the variances.- Parameters:
uniq- Adoublearray of length nvar containing the unique variances, wherenvaris the number of variables. If this member function is not called, the elements of uniq are set to 0.0. If the iterative methods fail for the unique variances used, new initial estimates should be tried. These may be obtained by use of another factoring method (use the final estimates from the new method as initial estimates in the old method). Another alternative is to call member functionsetVarianceEstimationMethodand set the input argument to 0. This will cause the initial unique variances to be estimated by the code.
-
-