- java.lang.Object
-
- com.imsl.stat.GARCH
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class GARCH extends Object implements Serializable, Cloneable
Computes estimates of the parameters of a GARCH(p,q) model.The Generalized Autoregressive Conditional Heteroskedastic (GARCH) model is defined as
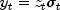
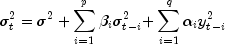
where
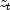 's are independent and identically
distributed standard normal random variables,
's are independent and identically
distributed standard normal random variables,
and
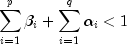
The above model is denoted as GARCH(p, q). The
\alpha_i, i=1,\ldots,q <\equation> and the \beta_j, j=1,\ldots,p <\equation> parameters will be called the ARCH and GARCH coefficients, respectively. When 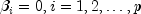 , the above model reduces
to ARCH(q) which was proposed by Engle (1982). That is, a GARCH(0,q) is equivalent
to the ARCH(q) model. The non-negativity conditions
on the parameters imply a nonnegative variance and the condition on the
sum of the
, the above model reduces
to ARCH(q) which was proposed by Engle (1982). That is, a GARCH(0,q) is equivalent
to the ARCH(q) model. The non-negativity conditions
on the parameters imply a nonnegative variance and the condition on the
sum of the 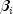 's and
's and 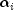 's
is required for wide sense stationarity.
's
is required for wide sense stationarity.In the empirical analysis of observed data, GARCH(1,1) or GARCH(1,2) models have often found to appropriately account for conditional heteroskedasticity (Palm 1996). This finding is similar to linear time series analysis based on ARMA models.
It is important to notice that for the above models positive and negative past values have a symmetric impact on the conditional variance. In practice, many series may have strong asymmetric influence on the conditional variance. To take into account this phenomena, Nelson (1991) put forward Exponential GARCH (EGARCH). Lai (1998) proposed and studied some properties of a general class of models that extended linear relationship of the conditional variance in ARCH and GARCH into nonlinear fashion.
The maximal likelihood method is used in estimating the parameters in GARCH(p,q). The log-likelihood of the model for the observed series
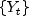 with length m is
with length m is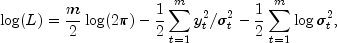
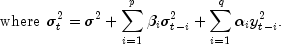
In the model, if q = 0, the model GARCH is singular such that the estimated Hessian matrix H is singular.
The initial values of the parameter array
![x[,,]](eqn_3143.png) entered in array
entered in array xguess[ ]must satisfy certain constraints. The first element ofxguessrefers to sigma and must be greater than zero and less thanmaxSigma. The remaining p+q initial values must each be greater than or equal to zero but less than one.To guarantee stationarity in model fitting,
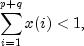
is checked internally. The initial values should be selected from the values between zero and one. The value of Akaike Information Criterion is computed by

where log(L) is the value of the log-likelihood function at the estimated parameters.
In fitting the optimal model, the class
MinConGenLin, is modified to find the maximal likelihood estimates of the parameters in the model. Statistical inferences can be performed outside of the classGARCHbased on the output of the log-likelihood function (getlogLikelihoodmethod), the Akaike Information Criterion (getAkaikemethod), and the variance-covariance matrix (getVarCovarMatrixmethod).- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classGARCH.ConstrInconsistentExceptionThe equality constraints are inconsistent.static classGARCH.EqConstrInconsistentExceptionThe equality constraints and the bounds on the variables are found to be inconsistent.static classGARCH.NoVectorXExceptionNo vector X satisfies all of the constraints.static classGARCH.TooManyIterationsExceptionNumber of function evaluations exceeded 1000.static classGARCH.VarsDeterminedExceptionThe variables are determined by the equality constraints.
-
Constructor Summary
Constructors Constructor and Description GARCH(int p, int q, double[] y, double[] xguess)Constructor forGARCH.
-
Method Summary
Methods Modifier and Type Method and Description voidcompute()Computes estimates of the parameters of a GARCH(p,q) model.doublegetAkaike()Returns the value of Akaike Information Criterion evaluated at the estimated parameter array.double[]getARCH()Returns the estimated values of the ARCH coefficients.double[]getGARCH()Returns the estimated values of the GARCH coefficients.doublegetLogLikelihood()Returns the value of Log-likelihood function evaluated at the estimated parameter array.doublegetSigma()Returns the estimated value of sigma squared.double[][]getVarCovarMatrix()Returns the variance-covariance matrix.double[]getX()Returns the estimated parameter array,x.voidsetMaxSigma(double maxSigma)Sets the value of the upperbound on the first element (sigma) of the array of returned estimated coefficients.
-
-
-
Constructor Detail
-
GARCH
public GARCH(int p, int q, double[] y, double[] xguess)Constructor forGARCH.- Parameters:
p- Anintscalar containing the number of GARCH parameters.q- Anintscalar containing the number of ARCH parameters.y- Adoublearray containing the observed time series data.xguess- Adoublearray of lengthp+q+ 1 containing the initial values for the parameter array.- Throws:
IllegalArgumentException- is thrown if the dimensions ofy, andxguessare not consistent.
-
-
Method Detail
-
compute
public final void compute() throws GARCH.ConstrInconsistentException, GARCH.EqConstrInconsistentException, GARCH.NoVectorXException, GARCH.TooManyIterationsException, GARCH.VarsDeterminedExceptionComputes estimates of the parameters of a GARCH(p,q) model.- Throws:
GARCH.ConstrInconsistentException- is thrown if the equality constraints are inconsistent.GARCH.EqConstrInconsistentException- is thrown if the equality constraints and the bounds on the variables are found to be inconsistent.GARCH.NoVectorXException- is thrown if no vector X satisfies all of the constraints.GARCH.TooManyIterationsException- is thrown if the number of function evaluations exceeded 1000.GARCH.VarsDeterminedException- is thrown if the variables are determined by the equality constraints.
-
getAkaike
public double getAkaike()
Returns the value of Akaike Information Criterion evaluated at the estimated parameter array. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the return value is0.- Returns:
- a
doublescalar containing the value of Akaike Information Criterion evaluated at the estimated parameter array.
-
getARCH
public double[] getARCH()
Returns the estimated values of the ARCH coefficients. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the method throws aNullPointerExceptionexception.- Returns:
- a
doublearray of sizeqcontaining the estimated values of the moving average (ARCH) coefficients.
-
getGARCH
public double[] getGARCH()
Returns the estimated values of the GARCH coefficients. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the method throws aNullPointerExceptionexception.- Returns:
- a
doublearray of sizepcontaining the estimated values of autoregressive (GARCH) parameters.
-
getLogLikelihood
public double getLogLikelihood()
Returns the value of Log-likelihood function evaluated at the estimated parameter array. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the return value is0.- Returns:
- a
doublescalar containing the value of Log-likelihood function evaluated at the estimated parameter array.
-
getSigma
public double getSigma()
Returns the estimated value of sigma squared. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the return value isNaN.- Returns:
- a
doublescalar containing the estimated value of sigma squared.
-
getVarCovarMatrix
public double[][] getVarCovarMatrix()
Returns the variance-covariance matrix. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the method throws aNullPointerExceptionexception.- Returns:
- a
doublematrix of sizep + q + 1byp + q + 1containing the variance-covariance matrix.
-
getX
public double[] getX()
Returns the estimated parameter array,x. Note that thecomputemethod must be invoked first before invoking this method. Otherwise, the method throws aNullPointerExceptionexception.- Returns:
- a
doublearray of size1 + q + pcontaining the estimated values of sigma squared, the ARCH parameters, and the GARCH parameters.
-
setMaxSigma
public void setMaxSigma(double maxSigma)
Sets the value of the upperbound on the first element (sigma) of the array of returned estimated coefficients.- Parameters:
maxSigma- Adoublescalar containing the value of the upperbound on the first element (sigma) of the array of returned estimated coefficients. Default = 10.
-
-