- java.lang.Object
-
- com.imsl.stat.HoltWintersExponentialSmoothing
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class HoltWintersExponentialSmoothing extends Object implements Serializable, Cloneable
Calculates parameters and forecasts using the Holt-Winters Multiplicative or Additive forecasting method for seasonal data.HoltWintersExponentialSmoothingperforms the Holt-Winters forecasting method to an equally spaced time series, where N =
where N = nobsand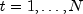 (or
(or 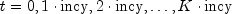 where
where 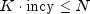 and
and  ). The
Holt-Winters procedure fits three component sequences known as the
level, the trend, and the seasonal sequence. There are
two formulations, depending on whether the seasonal component of the time
series is thought to be additive or multiplicative. The seasonal component
depends on the length of the season,
). The
Holt-Winters procedure fits three component sequences known as the
level, the trend, and the seasonal sequence. There are
two formulations, depending on whether the seasonal component of the time
series is thought to be additive or multiplicative. The seasonal component
depends on the length of the season, nseason= s, where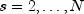 .
.Holt-Winters Additive Model
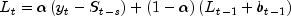
the level sequence 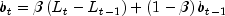
the trend sequence 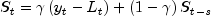
the seasonal sequence 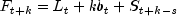
the forecast sequence Holt-Winters Multiplicative Model

the level sequence 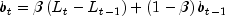
the trend sequence 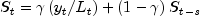
the seasonal sequence 
the forecast sequence Note that without a seasonal component, both the additive and multiplicative formulations reduce to the same methods. (The seasonal sequence is set to 1 for the multiplicative model, and identically 0 for the additive model.)
Default Starting Values
Initial values are required for these sequences. The software allows the user code to define these initial values (see
setInitialValuesmethod). If they are not provided, then the first two seasons of data are used: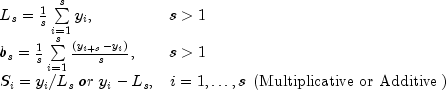
The smoothing parameters (
 ,
, 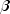 ,
, 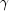 ) are each in the interval [0,1] and
can be specified by the user (see
) are each in the interval [0,1] and
can be specified by the user (see setParametersmethod), or automatically set by minimizing the within sample one-step ahead mean squared forecast error. Note that this objective function is not necessarily convex and solutions will depend on starting values. See Chatfield and Yar(1988) for further discussion. Starting values for ( ,
, 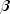 ,
, 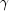 ) are
obtained by minimizing the mean squared error over
) are
obtained by minimizing the mean squared error over nsamplesbootstrap samples of the time series. Experiments suggest that this approach helps prevent poor starting values. Note, that solutions may vary for different settings of the number of random samples,nsamples.The return value of the
computemethod is an (N + 1) by 3 = (nobs+ 1) by 3 matrix containing the smoothing parameter values on the first row, followed by the calculated level, trend, and seasonal sequences. When N =nobsand s =nseason, the format of the return value is as follows:Series Storage Row Value 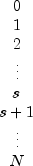

If one of the nonseasonal options is specifed, the return value will be (
nobs+ 1) by 2 or (nobs+ 1) by 1 accordingly.The variance-covariance matrix for the parameters (
 ,
, 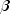 ,
, 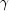 ) is
) is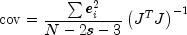
where
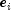 is the one-step-ahead forecast error,
and J is the Jacobian matrix of the series using the forecast model and
calculating forecasts one step ahead of each datum. Prediction intervals
are calculated following Chatfield and Yar (1991).
is the one-step-ahead forecast error,
and J is the Jacobian matrix of the series using the forecast model and
calculating forecasts one step ahead of each datum. Prediction intervals
are calculated following Chatfield and Yar (1991).- See Also:
- Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description HoltWintersExponentialSmoothing(int nseason, double[] y)Constructor forHoltWintersExponentialSmoothing.
-
Method Summary
Methods Modifier and Type Method and Description double[][]compute()Computes the values of the smoothing parameters.double[][]getForecasts()Returns the forecasts past the series data.double[]getSmoothedSeries()Returns the fitted series values.doublegetSumOfSquares()Returns the sum of squares of the one step ahead forecast errors.double[][]getVarCovarMatrix()Returns the variance-covariance matrix of the smoothing parameters estimated by minimizing the mean squared forecast error.voidsetAdditive()Specifies the use of the Additive time series model.voidsetConfidence(double confid)Sets the confidence level to use in the calculation of the prediction intervals.voidsetInitialValues(double[][] sequences)Sets the initial values for the level, trend, and seasonal component sequences.voidsetLowerBounds(double[] xlb)Sets the lower bounds for each of the smoothing parameters, ( ,
, 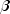 ,
, 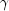 ).
).voidsetNonseasonalConstant()Remove the trend and the seasonal components and fit only the level component.voidsetNonseasonalTrend()Remove the seasonal component and fit only the level and trend components.voidsetNumberEval(int nsamples)Sets the number of evaluations of the residual norm that are sampled to obtain starting values for the smoothing parameters, ( ,
, 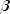 ,
, 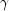 ).
).voidsetNumberForecasts(int nforecasts)Sets the number of forecasts desired past the series data.voidsetNumberOfObservations(int nobs)Sets the number of equally spaced series values.voidsetParameters(double[] params)Sets the values of the smoothing parameters for the level ( ), the trend (
), the trend (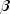 ), and the
seasonal (
), and the
seasonal (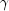 ) component sequences.
) component sequences.voidsetSeriesIncrement(int incy)Sets the constant stride through the series datay.voidsetUpperBounds(double[] xub)Sets the upper bounds for each of the smoothing parameters, ( ,
, 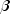 ,
, 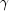 ).
).
-
-
-
Constructor Detail
-
HoltWintersExponentialSmoothing
public HoltWintersExponentialSmoothing(int nseason, double[] y)Constructor forHoltWintersExponentialSmoothing.- Parameters:
nseason- anintscalar containing the number of time points in a season, or the length of the season. The class requires that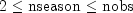 unless one of the non-seasonal
methods is used, in which case
unless one of the non-seasonal
methods is used, in which case nseasonis ignored. See thesetNonseasonalTrendandsetNonseasonalConstantmethods for details.y- adoublearray containing the values of the time series.
-
-
Method Detail
-
compute
public final double[][] compute()
Computes the values of the smoothing parameters.- Returns:
- an (
nobs+ 1) by 3doublematrix containing the values of the smoothing parameters followed by the level, trend, and seasonal component sequences. Note that if thesetNonseasonalTrendmethod is used, the matrix is of dimension (nobs+ 1) by 2 and if thesetNonseasonalConstantmethod is used, it is (nobs+ 1) by 1.
-
getForecasts
public double[][] getForecasts()
Returns the forecasts past the series data.- Returns:
- an
nforecastsby 1doublematrix containing the forecasts past the series data. The value of the i-th row is the forecast (i + 1) steps past the series data. IfsetConfidenceis used, the matrix will be of dimensionnforecastsby 3 and the value of the i-th row is the forecast (i+1) steps ahead followed by the prediction interval lower and upper bounds.
-
getSmoothedSeries
public double[] getSmoothedSeries()
Returns the fitted series values.- Returns:
- a
doublearray containing the fitted series values.
-
getSumOfSquares
public double getSumOfSquares()
Returns the sum of squares of the one step ahead forecast errors.- Returns:
- a
doublescalar containing the sum of squares of the one step ahead forecast errors.
-
getVarCovarMatrix
public double[][] getVarCovarMatrix()
Returns the variance-covariance matrix of the smoothing parameters estimated by minimizing the mean squared forecast error. The matrix is 3 by 3 unless thesetNonseasonalTrendmethod is used, in which case it is 2 by 2, or unless thesetNonseasonalConstantmethod is used, in which case it is 1 by 1. This method cannot be used together with thesetParametersmethod. Note that thecomputemethod must be invoked before invoking this method. Otherwise, the method throws aNullPointerExceptionexception.- Returns:
- a
doublematrix containing the variance-covariance matrix of the smoothing parameters estimated by minimizing the mean squared forecast error.
-
setAdditive
public void setAdditive()
Specifies the use of the Additive time series model. The Multiplicative model is the default.
-
setConfidence
public void setConfidence(double confid)
Sets the confidence level to use in the calculation of the prediction intervals.- Parameters:
confid- adoublescalar containing the confidence level to use in the calculation of the prediction intervals. If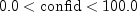 , prediction intervals are provided for each
forecast.
, prediction intervals are provided for each
forecast.
Default: Prediction intervals are not provided.
-
setInitialValues
public void setInitialValues(double[][] sequences)
Sets the initial values for the level, trend, and seasonal component sequences.- Parameters:
sequences- an (nobs+ 1) by 3doublematrix containing the initial values for the level , trend, and seasonal component sequences. The values must be stored in rows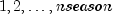 . Rows 0 and
. Rows 0 and
nseason+ 1 tonobsare ignored on input.sequences[0].lengthshould be equal to 3 unless thesetNonseasonalTrendmethod is used, in which case it is 2 containing initial values for level ( ) and the trend
(
) and the trend
(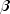 ). Likewise, if the
). Likewise, if the setNonseasonalConstantmethod is used,sequences[0].lengthis 1 and contains the initial values for the level parameter ( ) only.
) only.
Default: Initial values are computed by the function.
-
setLowerBounds
public void setLowerBounds(double[] xlb)
Sets the lower bounds for each of the smoothing parameters, ( ,
, 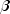 ,
, 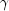 ).
).- Parameters:
xlb- adoublearray containing the lower bounds for each of the smoothing parameters, ( ,
,  ,
, 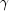 ). Note that the lower bounds must be in the
interval [0,1], inclusive. The array is ignored if the
). Note that the lower bounds must be in the
interval [0,1], inclusive. The array is ignored if the
setParametersmethod is used. The array should be length 3 unless thesetNonseasonalTrendmethod is used, in which case it is of length 2 containing lower bounds for level ( ) and
the trend (
) and
the trend (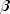 ) components.
Likewise, if the
) components.
Likewise, if the setNonseasonalConstantmethod is used,xlbis of length 1 and contains the lower bound for the level parameter ( ) component only.
) component only.
Default: Lower bounds are all 0.
-
setNonseasonalConstant
public void setNonseasonalConstant()
Remove the trend and the seasonal components and fit only the level component. If used, the models involve only the level ( ) parameter. The method is simple exponential
smoothing.
) parameter. The method is simple exponential
smoothing.
Default: The method includes all three components.
-
setNonseasonalTrend
public void setNonseasonalTrend()
Remove the seasonal component and fit only the level and trend components. If used, the models involve only the level ( ) and trend (
) and trend (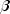 )
parameters. The method is equivalent to double exponential smoothing.
)
parameters. The method is equivalent to double exponential smoothing.
Default: The method includes all three components.
-
setNumberEval
public void setNumberEval(int nsamples)
Sets the number of evaluations of the residual norm that are sampled to obtain starting values for the smoothing parameters, ( ,
, 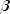 ,
, 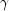 ).
).- Parameters:
nsamples- anintscalar containing the number of evaluations.Default:
nsamples=nobs.
-
setNumberForecasts
public void setNumberForecasts(int nforecasts)
Sets the number of forecasts desired past the series data.- Parameters:
nforecasts- anintscalar containing the number of forecasts desired past the series data.Default: No forecasts are computed past the series data.
-
setNumberOfObservations
public void setNumberOfObservations(int nobs)
Sets the number of equally spaced series values.- Parameters:
nobs- anintscalar containing the number of equally spaced series values.Default:
nobs=y.length.
-
setParameters
public void setParameters(double[] params)
Sets the values of the smoothing parameters for the level ( ), the trend (
), the trend (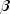 ), and the
seasonal (
), and the
seasonal (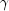 ) component sequences.
) component sequences.- Parameters:
params- adoublearray containing the values of the smoothing parameters for the level ( ), the trend (
), the trend (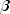 ),
and the seasonal (
),
and the seasonal (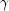 ) component
sequences. The array should be length 3 unless the
) component
sequences. The array should be length 3 unless the
setNonseasonalTrendmethod is used, in which case it is of length 2 containing values for level ( ) and the trend
(
) and the trend
(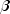 ) components. Likewise, if
the
) components. Likewise, if
the setNonseasonalConstantmethod is used,paramsis of length 1 and contains the value for the level parameter ( ) component only.
) component only.
Default: Parameter values are selected by minimizing the mean squared one step ahead forecast error.
-
setSeriesIncrement
public void setSeriesIncrement(int incy)
Sets the constant stride through the series datay.- Parameters:
incy- anintscalar containing the constant stride through the series datay.y.lengthmust be at least . When
. When
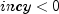 , the series is incremented
in reverse order beginning at index
, the series is incremented
in reverse order beginning at index 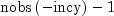 .
.
Default:
incy= 1.
-
setUpperBounds
public void setUpperBounds(double[] xub)
Sets the upper bounds for each of the smoothing parameters, ( ,
, 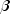 ,
, 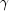 ).
).- Parameters:
xub- adoublearray containing the upper bounds for each of the smoothing parameters, ( ,
, 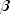 ,
, 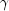 ). Note that the upper bounds must be in the
interval [0,1], inclusive. The array is ignored if the
). Note that the upper bounds must be in the
interval [0,1], inclusive. The array is ignored if the
setParametersmethod is used. The array should be length 3 unless thesetNonseasonalTrendmethod is used, in which case it is of length 2 containing upper bounds for level ( ) and
the trend (
) and
the trend (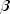 ) components.
Likewise, if the
) components.
Likewise, if the setNonseasonalConstantmethod is used,xubis of length 1 and contains the upper bound for the level parameter ( ) component only.
) component only.
Default: Upper bounds are all 1.
-
-