- java.lang.Object
-
- com.imsl.stat.LackOfFit
-
public class LackOfFit extends Object
Performs lack-of-fit test for a univariate time series or transfer function given the appropriate correlation function.LackOfFitmay be used to diagnose lack of fit in both ARMA and transfer function models. Typical arguments for these situations are:Model lagMinlagMaxnpFreeARMA (p, q) 1 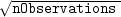
p + q Transfer function 0 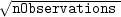
r + s LackOfFitperforms a portmanteau lack of fit test for a time series or transfer function containingnObservationsobservations given the appropriate sample correlation function for
k = L, L+1,...,K where L =
for
k = L, L+1,...,K where L =
lagMinand K =lagMax.The basic form of the test statistic Q is
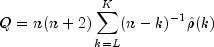
with L = 1 if
 is an autocorrelation function. Given that the model is adequate, Q
has a chi-squared distribution with
is an autocorrelation function. Given that the model is adequate, Q
has a chi-squared distribution with 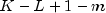 degrees of
freedom where m =
degrees of
freedom where m = npFreeis the number of parameters estimated in the model. If the mean of the time series is estimated, Woodfield (1990) recommends not including this in the count of the parameters estimated in the model. Thus, for an ARMA(p, q) model setnpFree= p + q regardless of whether the mean is estimated or not. The original derivation for time series models is due to Box and Pierce (1970) with the above modified version discussed by Ljung and Box (1978). The extension of the test to transfer function models is discussed by Box and Jenkins (1976, pages 394-395).- See Also:
- Example
-
-
Method Summary
Methods Modifier and Type Method and Description static double[]compute(int nObservations, double[] correlations, int npFree, int lagMax)Performs lack-of-fit test for a univariate time series or transfer function given the appropriate correlation function using a minimum lag of 1.static double[]compute(int nObservations, double[] correlations, int npFree, int lagMax, int lagMin)Performs lack-of-fit test for a univariate time series or transfer function given the appropriate correlation function.
-
-
-
Method Detail
-
compute
public static double[] compute(int nObservations, double[] correlations, int npFree, int lagMax)Performs lack-of-fit test for a univariate time series or transfer function given the appropriate correlation function using a minimum lag of 1.- Parameters:
nObservations- anintcontaining the number of observations of the stationary time series.correlations- adoublearray of lengthlagMax+1containing the correlation function.npFree- anintscalar specifying the number of free parameters in the formulation of the time series model.npfreemust be greater than or equal to zero and less thanlagMax. Woodfield (1990) recommendsnpFree = p + q.lagMax- anintscalar specifying the maximum lag of the correlation function.- Returns:
- a
doublearray of length 2 with the test statistic, Q, and its p-value, p. Under the null hypothesis, Q has an approximate chi-squared distribution withlagMax-lagMin+1-npFreedegrees of freedom.
-
compute
public static double[] compute(int nObservations, double[] correlations, int npFree, int lagMax, int lagMin)Performs lack-of-fit test for a univariate time series or transfer function given the appropriate correlation function.- Parameters:
nObservations- anintcontaining the number of observations of the stationary time series.correlations- adoublearray of lengthlagMax+1containing the correlation function.npFree- anintscalar specifying the number of free parameters in the formulation of the time series model.npfreemust be greater than or equal to zero and less thanlagMax. Woodfield (1990) recommendsnpFree = p + q.lagMax- anintscalar specifying the maximum lag of the correlation function.lagMin- anintscalar specifying the minimum lag of the correlation function.lagMincorresponds to the lower bound of summation in the lack of fit test statistic. Default value is 1.- Returns:
- a
doublearray of length 2 with the test statistic, Q, and its p-value, p. Under the null hypothesis, Q has an approximate chi-squared distribution withlagMax-lagMin+1-npFreedegrees of freedom.
-
-