- java.lang.Object
-
- com.imsl.stat.MultiCrossCorrelation
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class MultiCrossCorrelation extends Object implements Serializable, Cloneable
Computes the multichannel cross-correlation function of two mutually stationary multichannel time series.MultiCrossCorrelationestimates the multichannel cross-correlation function of two mutually stationary multichannel time series. Define the multichannel time series X by
where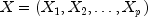
with n =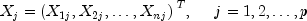
x.lengthand p =x[0].length. Similarly, define the multichannel time series Y by
where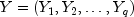
with m =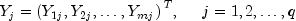
y.lengthand q =y[0].length. The columns of X and Y correspond to individual channels of multichannel time series and may be examined from a univariate perspective. The rows of X and Y correspond to observations of p-variate and q-variate time series, respectively, and may be examined from a multivariate perspective. Note that an alternative characterization of a multivariate time series X considers the columns to be observations of the multivariate time series while the rows contain univariate time series. For example, see Priestley (1981, page 692) and Fuller (1976, page 14).Let
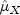 =
= xmeanbe the row vector containing the means of the channels of X. In particular,
where for j = 1, 2, ..., p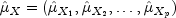
Let
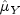 =
= ymeanbe similarly defined. The cross-covariance of lag k between channel i of X and channel j of Y is estimated by
where i = 1, ..., p, j = 1, ..., q, and K =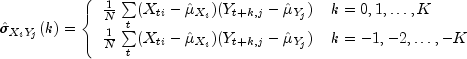
maximum_lag. The summation on t extends over all possible cross-products with N equal to the number of cross-products in the sum.Let
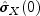 =
= xvar, wherexvaris the variance of X, be the row vector consisting of estimated variances of the channels of X. In particular,
where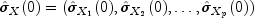
Let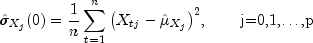
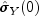 =
= yvar, whereyvaris the variance of Y, be similarly defined. The cross-correlation of lag k between channel i of X and channel j of Y is estimated by![hat rho _{X_jY_j}(k) = frac{hat sigma
_{{X_j}{Y_j}(k)}}{ {[ hatsigma _{X_i}(0)hatsigma _{X_j}(0)]}^{frac{1}{2}}}
;;;;;k =0,pm1,dots, pm K](eqn_2676.png)
- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classMultiCrossCorrelation.NonPosVariancesExceptionThe problem is ill-conditioned.
-
Constructor Summary
Constructors Constructor and Description MultiCrossCorrelation(double[][] x, double[][] y, int maximum_lag)Constructor to compute the multichannel cross-correlation function of two mutually stationary multichannel time series.
-
Method Summary
Methods Modifier and Type Method and Description double[][][]getCrossCorrelation()Returns the cross-correlations between the channels ofxandy.double[][][]getCrossCovariance()Returns the cross-covariances between the channels ofxandy.double[]getMeanX()Returns the mean of each channel ofx.double[]getMeanY()Returns the mean of each channel ofy.double[]getVarianceX()Returns the variances of the channels ofx.double[]getVarianceY()Returns the variances of the channels ofy.voidsetMeanX(double[] mean)Estimate of the mean of each channel ofx.voidsetMeanY(double[] mean)Estimate of the mean of each channel ofy.
-
-
-
Constructor Detail
-
MultiCrossCorrelation
public MultiCrossCorrelation(double[][] x, double[][] y, int maximum_lag)Constructor to compute the multichannel cross-correlation function of two mutually stationary multichannel time series.- Parameters:
x- A two-dimensionaldoublearray containing the first multichannel stationary time series. Each row ofxcorresponds to an observation of a multivariate time series and each column ofxcorresponds to a univariate time series.y- A two-dimensionaldoublearray containing the second multichannel stationary time series. Each row ofycorresponds to an observation of a multivariate time series and each column ofycorresponds to a univariate time series.maximum_lag- Anintcontaining the maximum lag of the cross-covariance and cross-correlations to be computed.maximum_lagmust be greater than or equal to 1 and less than the minimum number of observations ofxandy.
-
-
Method Detail
-
getCrossCorrelation
public double[][][] getCrossCorrelation() throws MultiCrossCorrelation.NonPosVariancesExceptionReturns the cross-correlations between the channels ofxandy.- Returns:
- A
doublearray of size 2 *maximum_lag+1 byx[0].lengthbyy[0].lengthcontaining the cross-correlations between the time seriesxandy. The cross-correlation between channel i of thexseries and channel j of theyseries at lag k, where k = -maximum_lag, ..., 0, 1, ...,maximum_lag, corresponds to output array element with index [k][i][j] where k= 0,1,...,(2*maximum_lag), i = 1, ...,x[0].length, and j = 1, ...,y[0].length. - Throws:
MultiCrossCorrelation.NonPosVariancesException
-
getCrossCovariance
public double[][][] getCrossCovariance() throws MultiCrossCorrelation.NonPosVariancesExceptionReturns the cross-covariances between the channels ofxandy.- Returns:
- A
doublearray of size 2 *maximum_lag+1 byx[0].lengthbyy[0].lengthcontaining the cross-covariances between the time seriesxandy. The cross-covariances between channel i of thexseries and channel j of theyseries at lag k where k = -maximum_lag, ..., 0, 1, ...,maximum_lag, corresponds to output array element with index [k][i][j] where k= 0,1,...,(2*maximum_lag), i = 1, ...,x[0].length, and j = 1, ...,y[0].length. - Throws:
MultiCrossCorrelation.NonPosVariancesException
-
getMeanX
public double[] getMeanX()
Returns the mean of each channel ofx.- Returns:
- A one-dimensional
doublecontaining the mean of each channel in the time seriesx.
-
getMeanY
public double[] getMeanY()
Returns the mean of each channel ofy.- Returns:
- A one-dimensional
doublecontaining the estimate mean of each channel in the time seriesy.
-
getVarianceX
public double[] getVarianceX() throws MultiCrossCorrelation.NonPosVariancesExceptionReturns the variances of the channels ofx.- Returns:
- A one-dimensional
doublecontaining the variances of each channel in the time seriesx. - Throws:
MultiCrossCorrelation.NonPosVariancesException
-
getVarianceY
public double[] getVarianceY() throws MultiCrossCorrelation.NonPosVariancesExceptionReturns the variances of the channels ofy.- Returns:
- A one-dimensional
doublecontaining the variances of each channel in the time seriesy. - Throws:
MultiCrossCorrelation.NonPosVariancesException
-
setMeanX
public void setMeanX(double[] mean)
Estimate of the mean of each channel ofx.- Parameters:
mean- A one-dimensionaldoublecontaining the estimate of the mean of each channel in time seriesx.
-
setMeanY
public void setMeanY(double[] mean)
Estimate of the mean of each channel ofy.- Parameters:
mean- A one-dimensionaldoublecontaining the estimate of the mean of each channel in the time seriesy.
-
-