- java.lang.Object
-
- com.imsl.stat.NonlinearRegression
-
public class NonlinearRegression extends Object
Fits a multivariate nonlinear regression model using least squares. The nonlinear regression model is
where the observed values of the
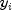 constitute the
responses or values of the dependent variable, the known
constitute the
responses or values of the dependent variable, the known 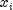 are vectors of values of the independent (explanatory)
variables,
are vectors of values of the independent (explanatory)
variables, 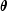 is the vector of
is the vector of 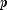 regression parameters, and the
regression parameters, and the 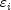 are independently distributed normal errors each with mean zero
and variance
are independently distributed normal errors each with mean zero
and variance 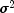 . For this model, a least squares
estimate of
. For this model, a least squares
estimate of  is also a maximum likelihood estimate
of
is also a maximum likelihood estimate
of  .
.
The residuals for the model are
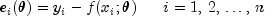
A value of
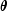 that minimizes
that minimizes![sumlimits_{i=1}^n[e_i(theta)]^2](eqn_2629.png)
is the least-squares estimate of
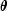 calculated by this class.
calculated by this class.
NonlinearRegressionaccepts these residuals one at a time as input from a user-supplied function. This allowsNonlinearRegressionto handle cases where is so large that data cannot reside in an array but must reside
in a secondary storage device.
is so large that data cannot reside in an array but must reside
in a secondary storage device.NonlinearRegressionis based on MINPACK routinesLMDIFandLMDERby More' et al. (1980).NonlinearRegressionuses a modified Levenberg-Marquardt method to generate a sequence of approximations to the solution. Let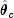 be the current estimate of
be the current estimate of 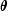 . A new estimate is
given by
. A new estimate is
given by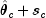
where
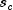 is a solution to
is a solution to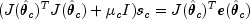
Here,
 is the Jacobian evaluated at
is the Jacobian evaluated at 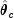 .
.
The algorithm uses a "trust region" approach with a step bound of
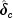 . A solution of the equations is first
obtained for
. A solution of the equations is first
obtained for 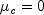 . If
. If 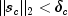 , this update is accepted; otherwise,
, this update is accepted; otherwise,
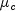 is set to a positive value and another solution
is obtained. The method is discussed by Levenberg (1944), Marquardt (1963),
and Dennis and Schnabel (1983, pages 129 - 147, 218 - 338).
is set to a positive value and another solution
is obtained. The method is discussed by Levenberg (1944), Marquardt (1963),
and Dennis and Schnabel (1983, pages 129 - 147, 218 - 338).Forward finite differences are used to estimate the Jacobian numerically unless the user supplied function computes the derivatives. In this case the Jacobian is computed analytically via the user-supplied function.
NonlinearRegressiondoes not actually store the Jacobian but uses fast Givens transformations to construct an orthogonal reduction of the Jacobian to upper triangular form. The reduction is based on fast Givens transformations (see Golub and Van Loan 1983, pages 156-162, Gentleman 1974). This method has two main advantages: (1) the loss of accuracy resulting from forming the crossproduct matrix used in the equations for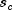 is avoided, and (2) the n x p
Jacobian need not be stored saving space when
is avoided, and (2) the n x p
Jacobian need not be stored saving space when 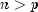 .
.
A weighted least squares fit can also be performed. This is appropriate when the variance of
 in the nonlinear
regression model is not constant but instead is
in the nonlinear
regression model is not constant but instead is 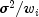 . Here,
. Here, 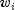 are weights input via the
user supplied function. For the weighted case,
are weights input via the
user supplied function. For the weighted case, NonlinearRegressionfinds the estimate by minimizing a weighted sum of squares error.Programming Notes
Nonlinear regression allows users to specify the model's functional form. This added flexibility can cause unexpected convergence problems for users who are unaware of the limitations of the algorithm. Also, in many cases, there are possible remedies that may not be immediately obvious. The following is a list of possible convergence problems and some remedies. There is not a one-to-one correspondence between the problems and the remedies. Remedies for some problems may also be relevant for the other problems.
- A local minimum is found. Try a different starting value. Good
starting values often can be obtained by fitting simpler models. For
example, for a nonlinear function
good starting values can be obtained from the estimated linear regression coefficients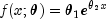
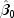 and
and
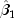 from a simple linear regression of
ln y on ln x. The starting values for the nonlinear regression
in this case would be
from a simple linear regression of
ln y on ln x. The starting values for the nonlinear regression
in this case would be
If an approximate linear model is unclear, then simplify the model by reducing the number of nonlinear regression parameters. For example, some nonlinear parameters for which good starting values are known could be set to these values. This simplifies the approach to computing starting values for the remaining parameters.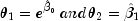
- The estimate of
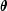 is incorrectly returned
as the same or very close to the initial estimate.
is incorrectly returned
as the same or very close to the initial estimate.
- The scale of the problem may be orders of
magnitude smaller than the assumed default of 1 causing
premature stopping. For example, if the sums of squares for
error is less than approximately
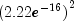 ,
the routine stops. See Example 3, which shows how to shut
down some of the stopping criteria that may not be relevant
for your particular problem and which also shows how to
improve the speed of convergence by the input of the scale
of the model parameters.
,
the routine stops. See Example 3, which shows how to shut
down some of the stopping criteria that may not be relevant
for your particular problem and which also shows how to
improve the speed of convergence by the input of the scale
of the model parameters. - The scale of the problem may be orders of
magnitude larger than the assumed default causing premature
stopping. The information with regard to the input of the
scale of the model parameters in Example 3 is also relevant
here. In addition, the maximum allowable step size (
setMaxStepsize(double)) in Example 3 may need to be increased. - The residuals are input with accuracy much less
than machine accuracy causing premature stopping because a
local minimum is found. Again see Example 3 to see generally
how to change some default tolerances. If you cannot improve
the precision of the computations of the residual, you need
to use method
setDigits(int)to indicate the actual number of good digits in the residuals.
- The scale of the problem may be orders of
magnitude smaller than the assumed default of 1 causing
premature stopping. For example, if the sums of squares for
error is less than approximately
- The model is discontinuous as a function of
 . There may be a mistake in the user-supplied function.
Note that the function
. There may be a mistake in the user-supplied function.
Note that the function 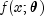 can be a
discontinuous function of x.
can be a
discontinuous function of x. - The R matrix returned by
getRis inaccurate. If only a function is supplied try providing theNonlinearRegression.Derivative. If the derivative is supplied try providing onlyNonlinearRegression.Function. - Overflow occurs during the computations. Make sure the user-supplied
functions do not overflow at some value of
 .
. - The estimate of
 is going to infinity. A
parameterization of the problem in terms of reciprocals may help.
is going to infinity. A
parameterization of the problem in terms of reciprocals may help.
- Some components of
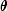 are outside known
bounds. This can sometimes be handled by making a function that
produces artificially large residuals outside of the bounds (even
though this introduces a discontinuity in the model function).
are outside known
bounds. This can sometimes be handled by making a function that
produces artificially large residuals outside of the bounds (even
though this introduces a discontinuity in the model function).
Note that the
solvemethod must be called prior to calling the "get" member functions, otherwise anullis returned. - A local minimum is found. Try a different starting value. Good
starting values often can be obtained by fitting simpler models. For
example, for a nonlinear function
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceNonlinearRegression.DerivativePublic interface for the user supplied function to compute the derivative forNonlinearRegression.static interfaceNonlinearRegression.FunctionPublic interface for the user supplied function forNonlinearRegression.static classNonlinearRegression.NegativeFreqExceptionA negative frequency was encountered.static classNonlinearRegression.NegativeWeightExceptionA negative weight was encountered.static classNonlinearRegression.TooManyIterationsExceptionThe number of iterations has exceeded the maximum allowed.
-
Constructor Summary
Constructors Constructor and Description NonlinearRegression(int nparm)Constructs a new nonlinear regression object.
-
Method Summary
Methods Modifier and Type Method and Description doublegetCoefficient(int i)Returns the estimate for a coefficient.double[]getCoefficients()Returns the regression coefficients.doublegetDFError()Returns the degrees of freedom for error.intgetErrorStatus()Gets information about the performance ofNonlinearRegression.double[][]getR()Returns a copy of theRmatrix.intgetRank()Returns the rank of the matrix.doublegetSSE()Returns the sums of squares for error.voidsetAbsoluteTolerance(double absoluteTolerance)Sets the absolute function tolerance.voidsetDigits(int nGood)Sets the number of good digits in the residuals.voidsetFalseConvergenceTolerance(double falseConvergenceTolerance)Sets the false convergence tolerance.voidsetGradientTolerance(double gradientTolerance)Sets the gradient tolerance used to compute the gradient.voidsetGuess(double[] thetaGuess)Sets the initial guess of the parameter valuesvoidsetInitialTrustRegion(double initialTrustRegion)Sets the initial trust region radius.voidsetMaxIterations(int maxIterations)Sets the maximum number of iterations allowed during optimizationvoidsetMaxStepsize(double maxStepsize)Sets the maximum allowable stepsize.voidsetRelativeTolerance(double relativeTolerance)Sets the relative function tolerancevoidsetScale(double[] scale)Sets the scaling array fortheta.voidsetStepTolerance(double stepTolerance)Sets the step tolerance used to step between two points.double[]solve(NonlinearRegression.Function F)Solves the least squares problem and returns the regression coefficients.
-
-
-
Constructor Detail
-
NonlinearRegression
public NonlinearRegression(int nparm)
Constructs a new nonlinear regression object.- Parameters:
nparm- Anintwhich specifies the number of unknown parameters in the regression.
-
-
Method Detail
-
getCoefficient
public double getCoefficient(int i)
Returns the estimate for a coefficient.- Parameters:
i- Anintwhich specifies the index of a coefficient whose estimate is to be returned.- Returns:
- A
doublewhich contains the estimate for the i-th coefficient ornullifsolvehas not been called.
-
getCoefficients
public double[] getCoefficients()
Returns the regression coefficients.- Returns:
- A
doublearray containing the regression coefficients ornullifsolvehas not been called.
-
getDFError
public double getDFError()
Returns the degrees of freedom for error.- Returns:
- A
doublewhich specifies the degrees of freedom for error ornullifsolvehas not been called.
-
getErrorStatus
public int getErrorStatus()
Gets information about the performance ofNonlinearRegression.- Returns:
- An
intspecifying information about convergence.Value Description 0 All convergence tests were met. 1 Scaled step tolerance was satisfied. The current point may be an approximate local solution, or the algorithm is making very slow progress and is not near a solution, or StepToleranceis too big.2 Scaled actual and predicted reductions in the function are less than or equal to the relative function convergence tolerance RelativeTolerance.3 Iterates appear to be converging to a noncritical point. Incorrect gradient information, a discontinuous function, or stopping tolerances being too tight may be the cause. 4 Five consecutive steps with the maximum stepsize have been taken. Either the function is unbounded below, or has a finite asymptote in some direction, or the maxStepsizeis too small. - See Also:
setRelativeTolerance(double),setStepTolerance(double),setMaxStepsize(double)
-
getR
public double[][] getR()
Returns a copy of theRmatrix.Ris the upper triangular matrix containing theRmatrix from a QR decomposition of the matrix of regressors.- Returns:
- A two dimensional
doublearray containing a copy of theRmatrix ornullifsolvehas not been called.
-
getRank
public int getRank()
Returns the rank of the matrix.- Returns:
- An
intwhich specifies the rank of the matrix ornullifsolvehas not been called.
-
getSSE
public double getSSE()
Returns the sums of squares for error.- Returns:
- A
doublewhich contains the sum of squares for error ornullifsolvehas not been called.
-
setAbsoluteTolerance
public void setAbsoluteTolerance(double absoluteTolerance)
Sets the absolute function tolerance.- Parameters:
absoluteTolerance- Adoublescalar value specifying the absolute function tolerance. The tolerance must be greater than or equal to zero. The default value is 4.93e-32.- Throws:
IllegalArgumentException- is thrown ifabsoluteToleranceis less than 0
-
setDigits
public void setDigits(int nGood)
Sets the number of good digits in the residuals.- Parameters:
nGood- Anintspecifying the number of good digits in the residuals. The number of digits must be greater than zero. The default value is 15.- Throws:
IllegalArgumentException- is thrown ifngoodis less than or equal to 0
-
setFalseConvergenceTolerance
public void setFalseConvergenceTolerance(double falseConvergenceTolerance)
Sets the false convergence tolerance.- Parameters:
falseConvergenceTolerance- Adoublescalar value specifying the false convergence tolerance. The tolerance must be greater than or equal to zero. The default value is 2.22e-14.- Throws:
IllegalArgumentException- is thrown iffalseConvergenceToleranceis less than 0
-
setGradientTolerance
public void setGradientTolerance(double gradientTolerance)
Sets the gradient tolerance used to compute the gradient.- Parameters:
gradientTolerance- Adoublespecifying the gradient tolerance used to compute the gradient. The tolerance must be greater than or equal to zero. The default value is 6.055e-6.- Throws:
IllegalArgumentException- is thrown ifgradientToleranceis less than 0
-
setGuess
public void setGuess(double[] thetaGuess)
Sets the initial guess of the parameter values- Parameters:
thetaGuess- Adoublearray of initial values for the parameters. The default value is an array of zeroes.
-
setInitialTrustRegion
public void setInitialTrustRegion(double initialTrustRegion)
Sets the initial trust region radius.- Parameters:
initialTrustRegion- Adoublescalar value specifying the initial trust region radius. The initial trust radius must be greater than zero. If this member function is not called, a default is set based on the initial scaled Cauchy step.- Throws:
IllegalArgumentException- is thrown ifinitialTrustRegionis less than or equal to 0
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Sets the maximum number of iterations allowed during optimization- Parameters:
maxIterations- Anintspecifying the maximum number of iterations allowed during optimization. The value must be greater than 0. The default value is 100.- Throws:
IllegalArgumentException- is thrown ifmaxIterationsis less than or equal to 0
-
setMaxStepsize
public void setMaxStepsize(double maxStepsize)
Sets the maximum allowable stepsize.- Parameters:
maxStepsize- A nonnegativedoublevalue specifying the maximum allowable stepsize. The maximum allowable stepsize must be greater than zero. If this member function is not called, maximum stepsize is set to a default value based on a scaledtheta.- Throws:
IllegalArgumentException- is thrown ifmaxStepsizeis less than or equal to 0
-
setRelativeTolerance
public void setRelativeTolerance(double relativeTolerance)
Sets the relative function tolerance- Parameters:
relativeTolerance- Adoublescalar value specifying the relative function tolerance. The relative function tolerance must be greater than or equal to zero. The default value is 1.0e-20.- Throws:
IllegalArgumentException- is thrown ifrelativeToleranceis less than 0
-
setScale
public void setScale(double[] scale)
Sets the scaling array fortheta.- Parameters:
scale- Adoublearray containing the scaling values for the parameters (theta). The elements of the scaling array must be greater than zero.scaleis used mainly in scaling the gradient and the distance between points. If good starting values ofthetaGuessare known and are nonzero, then a good choice isscale[i]=1.0/thetaGuess[i]. Otherwise, ifthetais known to be in the interval (-10.e5, 10.e5), setscale[i]=10.e-5. By default, the elements of the scaling array are set to 1.0.- Throws:
IllegalArgumentException- is thrown if any of the elements ofscaleis less than or equal to 0
-
setStepTolerance
public void setStepTolerance(double stepTolerance)
Sets the step tolerance used to step between two points.- Parameters:
stepTolerance- Adoublescalar value specifying the step tolerance used to step between two points. The step tolerance must be greater than or equal to zero. The default value is 3.667e-11.- Throws:
IllegalArgumentException- is thrown ifstepToleranceis less than 0
-
solve
public double[] solve(NonlinearRegression.Function F) throws NonlinearRegression.TooManyIterationsException, NonlinearRegression.NegativeFreqException, NonlinearRegression.NegativeWeightException
Solves the least squares problem and returns the regression coefficients.- Parameters:
F- ANonlinearRegression.Functionwhose coefficients are to be computed.- Returns:
- A
doublearray containing the regression coefficients. - Throws:
NonlinearRegression.TooManyIterationsException- is thrown when the number of allowed iterations is exceededNonlinearRegression.NegativeFreqException- is thrown when the specified frequency is negativeNonlinearRegression.NegativeWeightException- is thrown when the weight is negative
-
-