- java.lang.Object
-
- com.imsl.stat.NormTwoSample
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class NormTwoSample extends Object implements Serializable, Cloneable
Computes statistics for mean and variance inferences using samples from two normal populations.Class
NormTwoSamplecomputes statistics for making inferences about the means and variances of two normal populations, using independent samples inx1andx2. Missing values, that is, values equal to NaN (not a number), are excluded from the computations. For inferences concerning parameters of a single normal population, see classNormOneSample.Let
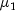 and
and  be
the mean and variance of the first population, and let
be
the mean and variance of the first population, and let
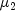 and
and 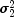 be the
corresponding quantities of the second population. The function contains
test confidence intervals for difference in means, equality of variances,
and the pooled variance.
be the
corresponding quantities of the second population. The function contains
test confidence intervals for difference in means, equality of variances,
and the pooled variance.The means and variances for the two samples are as follows:

and

Inferences about the Means
The test that the difference in means equals a certain value, for example,
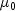 , depends on whether or not the variances
of the two populations can be considered equal. If the variances are equal
and
, depends on whether or not the variances
of the two populations can be considered equal. If the variances are equal
and meanHypothesisequals 0, the test is the two-sample t-test, which is equivalent to an analysis-of-variance test. The pooled variance for the difference-in-means test is as follows: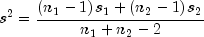
The t statistic is as follows:
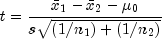
Also, the confidence interval for the difference in means can be obtained by first assigning the unequal variances flag to false. This can be done by calling the
setUnequalVariancesmethod. The confidence interval can then be obtained by thegetLowerCIDiffandgetUpperCIDiffmethods.If the population variances are not equal, the ordinary t statistic does not have a t distribution and several approximate tests for the equality of means have been proposed. (See, for example, Anderson and Bancroft 1952, and Kendall and Stuart 1979.) One of the earliest tests devised for this situation is the Fisher-Behrens test, based on Fisher's concept of fiducial probability. A procedure used in the
getTTest,getLowerCIDiffandgetUpperCIDiffmethods assuming unequal variances are specified is the Satterthwaite's procedure, as suggested by H.F. Smith and modified by F.E. Satterthwaite (Anderson and Bancroft 1952, p. 83). UsesetUnequalVariancestrue to obtain results assuming unequal variances.The test statistic is
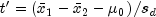
where
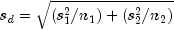
Under the null hypothesis of
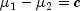 , this
quantity has an approximate t distribution with degrees of freedom
, this
quantity has an approximate t distribution with degrees of freedom
df, given by the following equation: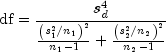
Inferences about Variances
The F statistic for testing the equality of variances is given by
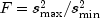 , where
, where
 is the larger of
is the larger of 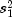 and
and 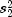 . If the variances are equal, this quantity
has an F distribution with
. If the variances are equal, this quantity
has an F distribution with 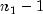 and
and
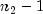 degrees of freedom.
degrees of freedom.It is generally not recommended that the results of the F test be used to decide whether to use the regular t-test or the modified
 on a single set of data. The modified
on a single set of data. The modified
 (Satterthwaite's procedure) is the more conservative
approach to use if there is doubt about the equality of the variances.
(Satterthwaite's procedure) is the more conservative
approach to use if there is doubt about the equality of the variances.- See Also:
- Example 1, Example 2, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description NormTwoSample(double[] x, double[] y)Constructor to compute statistics for mean and variance inferences using samples from two normal populations.
-
Method Summary
Methods Modifier and Type Method and Description voiddowndateX(double[] x)Removes the observations inxfrom the first sample.voiddowndateY(double[] y)Removes the observations inyfrom the second sample.doublegetChiSquaredTest()Returns the test statistic associated with the chi-squared test for common, or pooled, variances.intgetChiSquaredTestDF()Returns the degrees of freedom associated with the chi-squared test for the common, or pooled, variances.doublegetChiSquaredTestP()Returns the probability of a larger chi-squared associated with the chi-squared test for common, or pooled, variances.doublegetDiffMean()Returns the difference in means, mean ofx- mean ofy.doublegetFTest()Returns the F test value of the F test for equality of variances.intgetFTestDFdenominator()Returns the denominator degrees of freedom of the F test for equality of variances.intgetFTestDFnumerator()Returns the numerator degrees of freedom of the F test for equality of variances.doublegetFTestP()Returns the probability of a larger F in absolute value for the F test for equality of variances, assuming equal variances.doublegetLowerCICommonVariance()Returns the lower confidence limits for the common, or pooled, variance.doublegetLowerCIDiff()Returns the lower confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set by setUnequalVariances.doublegetLowerCIRatioVariance()Returns the approximate lower confidence limit for the ratio of the variance of the first population to the second.doublegetMeanX()Returns the mean of the first sample,x.doublegetMeanY()Returns the mean of the second sample,y.doublegetPooledVariance()Returns the Pooled variance for the two samples.doublegetStdDevX()Returns the standard deviation of the first sample.doublegetStdDevY()Returns the standard deviation of the second sample.doublegetTTest()Returns the test statistic for the Satterthwaite's approximation.doublegetTTestDF()Returns the degrees of freedom for the Satterthwaite's approximation for t-test for either equal or unequal variances, depending on the value set bysetUnequalVariances.doublegetTTestP()Returns the approximate probability of a largertfor the Satterthwaite's approximation for equal or unequal variances.doublegetUpperCICommonVariance()Returns the upper confidence limits for the common, or pooled, variance.doublegetUpperCIDiff()Returns the upper confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set bysetUnequalVariances.doublegetUpperCIRatioVariance()Returns the approximate upper confidence limit for the ratio of the variance of the first population to the second.voidsetChiSquaredTestNull(double varianceHypothesisValue)Sets the null hypothesis value for the chi-squared test.voidsetConfidenceMean(double confidenceMean)Sets the confidence level (in percent) for a two-sided interval estimate of the mean ofx- the mean ofy, in percent.voidsetConfidenceVariance(double confidenceVariance)Sets the confidence level (in percent) for two-sided interval estimate of the variances.voidsetTTestNull(double meanHypothesis)Sets the Null hypothesis value for t-test for the mean.voidsetUnequalVariances(boolean eqVar)Specifies whether to return statistics based on equal or unequal variances.voidupdate(double[] x, double[] y)Concatenates samples x and y to the samples provided in the constructor.voidupdateX(double[] x)Concatenates the values inxto the first sample provided in the constructor.voidupdateY(double[] y)Concatenates the values inyto the second sample provided in the constructor.
-
-
-
Constructor Detail
-
NormTwoSample
public NormTwoSample(double[] x, double[] y)Constructor to compute statistics for mean and variance inferences using samples from two normal populations.- Parameters:
x- is adoublearray containing the first sample.y- is adoublearray containing the second sample.
-
-
Method Detail
-
downdateX
public void downdateX(double[] x)
Removes the observations inxfrom the first sample.- Parameters:
x- is adoublearray containing the values to remove from the first sample.
-
downdateY
public void downdateY(double[] y)
Removes the observations inyfrom the second sample.- Parameters:
y- is adoublearray containing the values to remove from the second sample.
-
getChiSquaredTest
public double getChiSquaredTest()
Returns the test statistic associated with the chi-squared test for common, or pooled, variances. The chi-squared test is a test of the hypothesis where
where 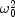 is the null hypothesis value as described in
is the null hypothesis value as described in setChiSquaredTestNull.- Returns:
- a
doublecontaining the test statistic for the chi-squared test.
-
getChiSquaredTestDF
public int getChiSquaredTestDF()
Returns the degrees of freedom associated with the chi-squared test for the common, or pooled, variances. The chi-squared test is a test of the hypothesis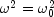 where
where
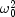 is the null hypothesis value as described in
is the null hypothesis value as described in
setChiSquaredTestNull.- Returns:
- an
intcontaining the degrees of freedom for the chi-squared test.
-
getChiSquaredTestP
public double getChiSquaredTestP()
Returns the probability of a larger chi-squared associated with the chi-squared test for common, or pooled, variances. The chi-squared test is a test of the hypothesis where
where 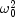 is the null hypothesis value as described in
is the null hypothesis value as described in
setChiSquaredTestNull.- Returns:
- a
doublecontaining the probability of a larger chi-squared for the chi-squared test for variances.
-
getDiffMean
public double getDiffMean()
Returns the difference in means, mean ofx- mean ofy.- Returns:
- a
doublecontaining the difference in mean.
-
getFTest
public double getFTest()
Returns the F test value of the F test for equality of variances.- Returns:
- a
doublecontaining the F test value of the F test for equality of variances.
-
getFTestDFdenominator
public int getFTestDFdenominator()
Returns the denominator degrees of freedom of the F test for equality of variances.- Returns:
- an
intcontaining the denominator degrees of freedom.
-
getFTestDFnumerator
public int getFTestDFnumerator()
Returns the numerator degrees of freedom of the F test for equality of variances.- Returns:
- an
intcontaining the numerator degrees of freedom.
-
getFTestP
public double getFTestP()
Returns the probability of a larger F in absolute value for the F test for equality of variances, assuming equal variances.- Returns:
- a
doublecontaining the probability of a larger F in absolute value, assuming equal variances.
-
getLowerCICommonVariance
public double getLowerCICommonVariance()
Returns the lower confidence limits for the common, or pooled, variance.- Returns:
- a
doublecontaining the lower confidence limits for the variance.
-
getLowerCIDiff
public double getLowerCIDiff()
Returns the lower confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set by setUnequalVariances.setUnequalVariances- Returns:
- a
doublecontaining the lower confidence limit for the mean of the first sample minus the mean of the second sample.
-
getLowerCIRatioVariance
public double getLowerCIRatioVariance()
Returns the approximate lower confidence limit for the ratio of the variance of the first population to the second.- Returns:
- a
doublecontaining the approximate lower confidence limit variance.
-
getMeanX
public double getMeanX()
Returns the mean of the first sample,x.- Returns:
- a
doublecontaining the mean.
-
getMeanY
public double getMeanY()
Returns the mean of the second sample,y.- Returns:
- a
doublecontaining the mean.
-
getPooledVariance
public double getPooledVariance()
Returns the Pooled variance for the two samples.- Returns:
- a
doublecontaining the Pooled variance for the two samples.
-
getStdDevX
public double getStdDevX()
Returns the standard deviation of the first sample.- Returns:
- a
doublecontaining the standard deviation of the first sample.
-
getStdDevY
public double getStdDevY()
Returns the standard deviation of the second sample.- Returns:
- a
doublecontaining the standard deviation of the second sample.
-
getTTest
public double getTTest()
Returns the test statistic for the Satterthwaite's approximation. The value returned will be based on assumption of equal or unequal variances based on the the value set bysetUnequalVariances.setUnequalVariances- Returns:
- a
doublecontaining the test statistic for the t-test.
-
getTTestDF
public double getTTestDF()
Returns the degrees of freedom for the Satterthwaite's approximation for t-test for either equal or unequal variances, depending on the value set bysetUnequalVariances.setUnequalVariances- Returns:
- an
doublecontaining the degrees of freedom for the t-test.
-
getTTestP
public double getTTestP()
Returns the approximate probability of a largertfor the Satterthwaite's approximation for equal or unequal variances.setUnequalVariances- Returns:
- a
doublecontaining the probability for the t-test.
-
getUpperCICommonVariance
public double getUpperCICommonVariance()
Returns the upper confidence limits for the common, or pooled, variance.- Returns:
- a
doublecontaining the upper confidence limits for the variance.
-
getUpperCIDiff
public double getUpperCIDiff()
Returns the upper confidence limit for the mean of the first population minus the mean of the second for equal or unequal variances depending on the value set bysetUnequalVariances.setUnequalVariances- Returns:
- a
doublecontaining the upper confidence limit for the mean of the first sample minus the mean of the second sample.
-
getUpperCIRatioVariance
public double getUpperCIRatioVariance()
Returns the approximate upper confidence limit for the ratio of the variance of the first population to the second.- Returns:
- a
doublecontaining the approximate upper confidence limit variance.
-
setChiSquaredTestNull
public void setChiSquaredTestNull(double varianceHypothesisValue)
Sets the null hypothesis value for the chi-squared test. The default is 1.0.- Parameters:
varianceHypothesisValue- adoublecontaining the null hypothesis value for the chi-squared test.
-
setConfidenceMean
public void setConfidenceMean(double confidenceMean)
Sets the confidence level (in percent) for a two-sided interval estimate of the mean ofx- the mean ofy, in percent. ArgumentconfidenceMeanmust be between 0.0 and 1.0 and is often 0.90, 0.95 or 0.99. For a one-sided confidence interval with confidence level c (at least 50 percent), set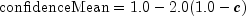 .
If the confidence mean is not specified, a 95-percent confidence interval
is computed.
Default: confidenceMean = .95
.
If the confidence mean is not specified, a 95-percent confidence interval
is computed.
Default: confidenceMean = .95- Parameters:
confidenceMean-doublecontaining the confidence level of the mean.
-
setConfidenceVariance
public void setConfidenceVariance(double confidenceVariance)
Sets the confidence level (in percent) for two-sided interval estimate of the variances. Under the assumption of equal variances, the pooled variance is used to obtain a two-sidedconfidenceVariancepercent confidence interval for the common variance withgetLowerCICommonVarianceorgetUpperCICommonVariance. Without making the assumption of equal variances,setUnequalVariances, the ratio of the variances is of interest. A two-sidedconfidenceVariancepercent confidence interval for the ratio of the variance of the first sample to that of the second sample is given by thegetLowerCIRatioVarianceandgetUpperCIRatioVariance. SeesetUnequalVariancesandgetUpperCIRatioVariance. The confidence intervals are symmetric in probability. ArgumentconfidenceVariancemust be between 0.0 and 1.0 and is often 0.90, 0.95 or 0.99. The default is 0.95.- Parameters:
confidenceVariance-doublecontaining the confidence level of the variance.
-
setTTestNull
public void setTTestNull(double meanHypothesis)
Sets the Null hypothesis value for t-test for the mean.meanHypothesis=0.0 by default.- Parameters:
meanHypothesis-doublecontaining the hypothesis value.
-
setUnequalVariances
public void setUnequalVariances(boolean eqVar)
Specifies whether to return statistics based on equal or unequal variances. The default is to return statistics for equal variances. ifeqVaris True then statistics for unequal variances will be returned.- Parameters:
eqVar- abooleancontaining a true or false value. A value of true will cause results for unequal variances to be returned. A value of false will cause results for equal variances to be returned.
-
update
public void update(double[] x, double[] y)Concatenates samples x and y to the samples provided in the constructor.This method updates the test results to include a new subset of the data. This is useful when the data is too large to fit into memory or when all of the data is not available at one time or location.
- Parameters:
x- is adoublearray containing updates to the first sample.y- is adoublearray containing updates to the second sample.
-
updateX
public void updateX(double[] x)
Concatenates the values inxto the first sample provided in the constructor.This method updates the test results to include a new subset of the data. This is useful when the data is too large to fit into memory or when all of the data is not available at one time or location.
- Parameters:
x- is adoublearray containing updates for the first sample.
-
updateY
public void updateY(double[] y)
Concatenates the values inyto the second sample provided in the constructor.This method updates the test results to include a new subset of the data. This is useful when the data is too large to fit into memory or when all of the data is not available at one time or location.
- Parameters:
y- is adoublearray containing updates for the second sample.
-
-