- java.lang.Object
-
- com.imsl.stat.NormalityTest
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class NormalityTest extends Object implements Serializable, Cloneable
Performs a test for normality.Three methods are provided for testing normality: the Shapiro-Wilk W test, the Lilliefors test, and the chi-squared test.
Shapiro-Wilk W Test
The Shapiro-Wilk W test is thought by D'Agostino and Stevens (1986, p. 406) to be one of the best omnibus tests of normality. The function is based on the approximations and code given by Royston (1982a, b, c). It can be used in samples as large as 2,000 or as small as 3. In the Shapiro and Wilk test, W is given by

where
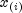 is the i-th largest order
statistic and x is the sample mean. Royston (1982)
gives approximations and tabled values that can be used to compute the
coefficients
is the i-th largest order
statistic and x is the sample mean. Royston (1982)
gives approximations and tabled values that can be used to compute the
coefficients 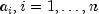 , and obtains the
significance level of the W statistic.
, and obtains the
significance level of the W statistic.Lilliefors Test
This function computes Lilliefors test and its p-values for a normal distribution in which both the mean and variance are estimated. The one-sample, two-sided Kolmogorov-Smirnov statistic D is first computed. The p-values are then computed using an analytic approximation given by Dallal and Wilkinson (1986). Because Dallal and Wilkinson give approximations in the range (0.01, 0.10) if the computed probability of a greater D is less than 0.01, the p-value is set to 0.50. Note that because parameters are estimated, p-values in Lilliefors test are not the same as in the Kolmogorov-Smirnov Test.
Observations should not be tied. If tied observations are found, an informational message is printed. A general reference for the Lilliefors test is Conover (1980). The original reference for the test for normality is Lilliefors (1967).
Chi-Squared Test
This function computes the chi-squared statistic, its p-value, and the degrees of freedom of the test. Argument n finds the number of intervals into which the observations are to be divided. The intervals are equiprobable except for the first and last interval, which are infinite in length.
If more flexibility is desired for the specification of intervals, the same test can be performed with class
ChiSquaredTest.- See Also:
- Example, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classNormalityTest.NoVariationInputExceptionThere is no variation in the input data.
-
Constructor Summary
Constructors Constructor and Description NormalityTest(double[] x)Constructor forNormalityTest.
-
Method Summary
Methods Modifier and Type Method and Description doubleChiSquaredTest(int n)Performs the chi-squared goodness-of-fit test.doublegetChiSquared()Returns the chi-square statistic for the chi-squared goodness-of-fit test.doublegetDegreesOfFreedom()Returns the degrees of freedom for the chi-squared goodness-of-fit test.doublegetMaxDifference()Returns the maximum absolute difference between the empirical and the theoretical distributions for the Lilliefors test.doublegetShapiroWilkW()Returns the Shapiro-Wilk W statistic for the Shapiro-Wilk W test.doubleLillieforsTest()Performs the Lilliefors test.doubleShapiroWilkWTest()Performs the Shapiro-Wilk W test.
-
-
-
Constructor Detail
-
NormalityTest
public NormalityTest(double[] x)
Constructor forNormalityTest.- Parameters:
x- Adoublearray containing the observations.x.lengthmust be in the range from 3 to 2,000, inclusive, for the Shapiro-Wilk W test and must be greater than 4 for the Lilliefors test.
-
-
Method Detail
-
ChiSquaredTest
public final double ChiSquaredTest(int n) throws NormalityTest.NoVariationInputException, InverseCdf.DidNotConvergeExceptionPerforms the chi-squared goodness-of-fit test.- Parameters:
n- Anintscalar containing the number of cells into which the observations are to be tallied.- Returns:
- A
doublescalar containing the p-value for the chi-squared goodness-of-fit test. - Throws:
NormalityTest.NoVariationInputException- is thrown if there is no variation in the input data.DidNotConvergeException- is thrown if the iteration did not converge.InverseCdf.DidNotConvergeException- See Also:
ChiSquaredTest
-
getChiSquared
public double getChiSquared()
Returns the chi-square statistic for the chi-squared goodness-of-fit test.- Returns:
- A
doublescalar containing the chi-square statistic. ReturnsDouble.NaNfor other tests.
-
getDegreesOfFreedom
public double getDegreesOfFreedom()
Returns the degrees of freedom for the chi-squared goodness-of-fit test.- Returns:
- A
doublescalar containing the degrees of freedom. ReturnsDouble.NaNfor other tests.
-
getMaxDifference
public double getMaxDifference()
Returns the maximum absolute difference between the empirical and the theoretical distributions for the Lilliefors test.- Returns:
- A
doublescalar containing the maximum absolute difference between the empirical and the theoretical distributions. ReturnsDouble.NaNfor other tests.
-
getShapiroWilkW
public double getShapiroWilkW()
Returns the Shapiro-Wilk W statistic for the Shapiro-Wilk W test.- Returns:
- A
doublescalar containing the Shapiro-Wilk W statistic. ReturnsDouble.NaNfor other tests.
-
LillieforsTest
public final double LillieforsTest() throws NormalityTest.NoVariationInputException, InverseCdf.DidNotConvergeExceptionPerforms the Lilliefors test.- Returns:
- A
doublescalar containing the p-value for the Lilliefors test. Probabilities less than 0.01 are reported as 0.01, and probabilities greater than 0.10 for the normal distribution are reported as 0.5. Otherwise, an approximate probability is computed. - Throws:
NormalityTest.NoVariationInputException- is thrown if there is no variation in the input data.DidNotConvergeException- is thrown if the iteration did not converge.InverseCdf.DidNotConvergeException
-
ShapiroWilkWTest
public final double ShapiroWilkWTest() throws NormalityTest.NoVariationInputException, InverseCdf.DidNotConvergeExceptionPerforms the Shapiro-Wilk W test.- Returns:
- A
doublescalar containing the p-value for the Shapiro-Wilk W test. - Throws:
NormalityTest.NoVariationInputException- is thrown if there is no variation in the input data.DidNotConvergeException- is thrown if the iteration did not converge.InverseCdf.DidNotConvergeException
-
-