- java.lang.Object
-
- com.imsl.stat.ProportionalHazards
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class ProportionalHazards extends Object implements Serializable, Cloneable
Analyzes survival and reliability data using Cox's proportional hazards model.Class
ProportionalHazardscomputes parameter estimates and other statistics in Proportional Hazards Generalized Linear Models. These models were first proposed by Cox (1972). Two methods for handling ties are allowed. Time-dependent covariates are not allowed. The user is referred to Cox and Oakes (1984), Kalbfleisch and Prentice (1980), Elandt-Johnson and Johnson (1980), Lee (1980), or Lawless (1982), among other texts, for a thorough discussion of the Cox proportional hazards model.Let
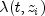 represent the hazard rate at
time t for observation number i with covariables contained as
elements of row vector
represent the hazard rate at
time t for observation number i with covariables contained as
elements of row vector 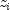 . The basic assumption in the
proportional hazards model (the proportionality assumption) is that the hazard
rate can be written as a product of a time varying function
. The basic assumption in the
proportional hazards model (the proportionality assumption) is that the hazard
rate can be written as a product of a time varying function
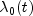 , which depends only on time, and a
function
, which depends only on time, and a
function 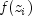 , which depends only on the covariable
values. The function
, which depends only on the covariable
values. The function 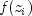 used in
used in
ProportionalHazardsis given as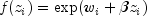 where
where 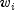 is a fixed constant assigned to the observation,
and b is a vector of coefficients to be estimated. With this function
one obtains a hazard rate
is a fixed constant assigned to the observation,
and b is a vector of coefficients to be estimated. With this function
one obtains a hazard rate
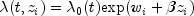 .
The form of
.
The form of 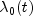 is not important in proportional
hazards models.
is not important in proportional
hazards models.The constants
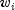 may be known theoretically. For
example, the hazard rate may be proportional to a known length or area, and
the
may be known theoretically. For
example, the hazard rate may be proportional to a known length or area, and
the 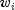 can then be determined from this known length or
area. Alternatively, the
can then be determined from this known length or
area. Alternatively, the  may be used to fix a subset
of the coefficients
may be used to fix a subset
of the coefficients 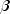 (say,
(say, 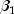 )
at specified values. When
)
at specified values. When 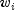 is used in this way,
constants
is used in this way,
constants  are used, while the
remaining coefficients in
are used, while the
remaining coefficients in 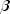 are free to vary in the
optimization algorithm. Constants are defined as 0.0 by default. If
user-specified constants are desired, use the
are free to vary in the
optimization algorithm. Constants are defined as 0.0 by default. If
user-specified constants are desired, use the setConstantColumnmethod to specify which column contains the constant.With this definition of
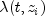 , the usual
partial (or marginal, see Kalbfleisch and Prentice (1980)) likelihood becomes
, the usual
partial (or marginal, see Kalbfleisch and Prentice (1980)) likelihood becomes
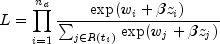
where
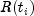 denotes the set of indices of
observations that have not yet failed at time
denotes the set of indices of
observations that have not yet failed at time 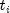 (the
risk set),
(the
risk set), 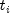 denotes the time of failure for the i-th
observation,
denotes the time of failure for the i-th
observation, 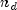 is the total number of observations
that fail. Right-censored observations (i.e., observations that are known to
have survived to time
is the total number of observations
that fail. Right-censored observations (i.e., observations that are known to
have survived to time 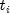 , but for which no time of
failure is known) are incorporated into the likelihood through the risk set
, but for which no time of
failure is known) are incorporated into the likelihood through the risk set
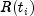 . Such observations never appear in the numerator
of the likelihood. When
. Such observations never appear in the numerator
of the likelihood. When setTieOptionsis set toBRESLOWS_APPROXIMATE(the default), all observations that are censored at time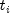 are not included in
are not included in  ,
while all observations that fail at time
,
while all observations that fail at time 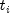 are
included in
are
included in  .
.If it can be assumed that the dependence of the hazard rate upon the covariate values remains the same from stratum to stratum, while the time-dependent term,
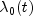 , may be different in
different strata, then
, may be different in
different strata, then ProportionalHazardsallows the incorporation of strata into the likelihood as follows. Let k index the m strata (set withsetStratumColumn). Then, the likelihood is given by![L_S=prod_{k=1}^{m}left [ prod_{i=1}^{n_k}frac{textup{exp}(w_{ki}+beta z_{ki})}{sum_{jin R(t_{ki})}^{}textup{exp}(w_{kj}+beta z_{kj})} right ]](eqn_2408.png)
In
ProportionalHazards, the log of the likelihood is maximized with respect to the coefficients . A
quasi-Newton algorithm approximating the Hessian via the matrix of sums of
squares and cross products of the first partial derivatives is used in the
initial iterations. When the change in the log-likelihood from one iteration
to the next is less than 100 times the convergence tolerance,
Newton-Raphson iteration is used. If, during any iteration, the
initial step does not lead to an increase in the log-likelihood, then step
halving is employed to find a step that will increase the log-likelihood.
. A
quasi-Newton algorithm approximating the Hessian via the matrix of sums of
squares and cross products of the first partial derivatives is used in the
initial iterations. When the change in the log-likelihood from one iteration
to the next is less than 100 times the convergence tolerance,
Newton-Raphson iteration is used. If, during any iteration, the
initial step does not lead to an increase in the log-likelihood, then step
halving is employed to find a step that will increase the log-likelihood.Once the maximum likelihood estimates have been computed, the algorithm computes estimates of a probability associated with each failure. Within stratum k, an estimate of the probability that the i-th observation fails at time
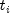 given the risk set
given the risk set
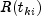 is given by
is given by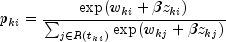
A diagnostic "influence" or "leverage" statistic is computed for each noncensored observation as:
where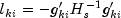
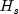 is the matrix of second partial derivatives
of the log-likelihood, and
is the matrix of second partial derivatives
of the log-likelihood, and
is computed as: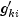
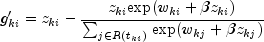
Influence statistics are not computed for censored observations.
A "residual" is computed for each of the input observations according to methods given in Cox and Oakes (1984, page 108). Residuals are computed as
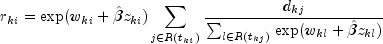
where
 is the number of tied failures in group
k at time
is the number of tied failures in group
k at time 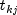 . Assuming that the proportional
hazards assumption holds, the residuals should approximate a random sample
(with censoring) from the unit exponential distribution. By subtracting the
expected values, centered residuals can be obtained. (The j-th
expected order statistic from the unit exponential with censoring is given as
. Assuming that the proportional
hazards assumption holds, the residuals should approximate a random sample
(with censoring) from the unit exponential distribution. By subtracting the
expected values, centered residuals can be obtained. (The j-th
expected order statistic from the unit exponential with censoring is given as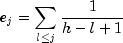
where h is the sample size, and censored observations are not included in the summation.)
An estimate of the cumulative baseline hazard within group k is given as

The observation proportionality constant is computed as
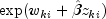
Note that the user can use the JDK JAVA Logging API to generate intermediate output for the solver. Accumulated levels of detail correspond to JAVA's FINE, FINER, and FINEST logging levels with FINE yielding the smallest amount of information and FINEST yielding the most. The levels of output yield the following:
Level Output FINE Logging is enabled, but observational statistics are not printed. FINER All output statistics are printed. FINEST Tracks progress through internal methods. - See Also:
- Example , Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classProportionalHazards.ClassificationVariableLimitExceptionThe Classification Variable limit set by the user throughsetUpperBoundhas been exceeded.
-
Field Summary
Fields Modifier and Type Field and Description static intBRESLOWS_APPROXIMATEBreslows approximate method of handling ties.static intSORTED_AS_PER_OBSERVATIONSFailures are assumed to occur in the same order as the observations input inx.
-
Constructor Summary
Constructors Constructor and Description ProportionalHazards(double[][] x, int[] nVarEffects, int[] indEffects)Constructor forProportionalHazards.
-
Method Summary
Methods Modifier and Type Method and Description double[][]getCaseStatistics()Returns the case statistics for each observation.intgetCensorColumn()Returns the column index ofxcontaining the optional censoring code for each observation.int[]getClassValueCounts()Returns the number of values taken by each classification variable.double[]getClassValues()Returns the class values taken by each classification variable.intgetConstantColumn()Returns the column index ofxcontaining the constant to be added to the linear response.doublegetConvergenceTol()Returns the convergence tolerance used.intgetFrequencyColumn()Returns the column index ofxcontaining the frequency of response for each observation.double[]getGradient()Returns the inverse of the Hessian times the gradient vector, computed at the initial estimates.double[][]getHessian()Returns the inverse of the Hessian of the negative of the log-likelihood, computed at the initial estimates.booleangetHessianOption()Returns thebooleanused to indicate whether or not to compute the Hessian and gradient at the initial estimates.double[]getInitialEstimates()Gets the initial parameter estimates.double[]getLastUpdates()Gets the last parameter updates.LoggergetLogger()Returns the logger object and enables logging.intgetMaxClass()Returns the upper bound used on the sum of the number of distinct values found among the classification variables inx.doublegetMaximumLikelihood()Returns the maximized log-likelihood.intgetMaxIterations()Return the maximum number of iterations allowed.double[]getMeans()Returns the means of the design variables.intgetNumberOfCoefficients()Returns the number of estimated coefficients in the model.intgetNumberRowsMissing()Returns the number of rows of data inxthat contain missing values in one or more specific columns ofx.double[][]getParameterStatistics()Returns the parameter estimates and associated statistics.intgetResponseColumn()Returns the column index ofxcontaining the response time for each observation.intgetStratumColumn()Returns the column index ofxcontaining the stratum number for each observation.int[]getStratumNumbers()Returns the stratum number used for each observation.doublegetStratumRatio()Returns the ratio at which a stratum is split into two strata.intgetTiesOption()Returns the method used for handling ties.double[][]getVarianceCovarianceMatrix()Returns the estimated asymptotic variance-covariance matrix of the parameters.voidsetCensorColumn(int censorIndex)Sets the column index ofxcontaining the optional censoring code for each observation.voidsetClassVarColumns(int[] classVarIndices)Sets the column indices ofxthat are the classification variables.voidsetConstantColumn(int fixedIndex)Sets the column index ofxcontaining the constant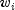 to be added
to the linear response.
to be added
to the linear response.voidsetConvergenceTol(double convergenceTol)Set the convergence tolerance.voidsetFrequencyColumn(int frequencyIndex)Sets the column index ofxcontaining the frequency of response for each observation.voidsetHessianOption(boolean wantHessian)Set the option to have the Hessian and gradient be computed at the initial estimates.voidsetInitialEstimates(double[] initialCoef)Sets the initial parameter estimates.voidsetMaxClass(int maxClass)Sets an upper bound on the sum of the number of distinct values found among the classification variables inx.voidsetMaxIterations(int maxIterations)Set the maximum number of iterations allowed.voidsetResponseColumn(int responseIndex)Sets the column index ofxcontaining the response variable.voidsetStratumColumn(int stratumIndex)Sets the column index ofxcontaining the stratification variable.voidsetStratumRatio(double stratumRatio)Set the ratio at which a stratum is split into two strata.voidsetTiesOption(int iTie)Sets the method for handling ties.
-
-
-
Field Detail
-
BRESLOWS_APPROXIMATE
public static final int BRESLOWS_APPROXIMATE
Breslows approximate method of handling ties. SeesetTiesOption.- See Also:
- Constant Field Values
-
SORTED_AS_PER_OBSERVATIONS
public static final int SORTED_AS_PER_OBSERVATIONS
Failures are assumed to occur in the same order as the observations input inx. The observations inxmust be sorted from largest to smallest failure time within each stratum, and grouped by stratum. All observations are treated as if their failure/censoring times were distinct when computing the log-likelihood. SeesetTiesOption.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
ProportionalHazards
public ProportionalHazards(double[][] x, int[] nVarEffects, int[] indEffects)Constructor forProportionalHazards.- Parameters:
x- adoublematrix containing the data, including optional data.nVarEffects- anintarray containing the number of variables associated with each effect in the model.indEffects- anintarray containing the column numbers ofxassociated with each effect. The firstnVarEffects[0]elements ofindEffectscontain the column numbers ofxfor the variables in the first effect. The nextnVarEffects[1]elements ofindEffectscontain the column numbers ofxfor the variables in the second effect, etc.
-
-
Method Detail
-
getCaseStatistics
public double[][] getCaseStatistics() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the case statistics for each observation.There is one row for each observation, and the columns of the returned matrix contain the following:
Column Statistic 0Estimated survival probability at the observation time. 1Estimated observation influence or leverage. 2A residual estimate. 3Estimated cumulative baseline hazard rate. 4Observation proportionality constant. - Returns:
- a
doublematrix containing the case statistics. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getCensorColumn
public int getCensorColumn()
Returns the column index ofxcontaining the optional censoring code for each observation.- Returns:
- an
intspecifying the column index ofxcontaining the optional censoring code for each observation.
-
getClassValueCounts
public int[] getClassValueCounts() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the number of values taken by each classification variable. The i-th element of the returned array is the number of distinct values taken by the i-th classification variable.- Returns:
- an
intarray containing the number of values taken by each classification variable. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getClassValues
public double[] getClassValues() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the class values taken by each classification variable. For description purposes, let
nclval =getClassValueCounts(). Then the first nclval[0] elements contain the values for the first classification variable, the next nclval[1] elements contain the values for the second classification variable, etc.- Returns:
- a
doublearray containing the values taken by each classification variable. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getConstantColumn
public int getConstantColumn()
Returns the column index ofxcontaining the constant to be added to the linear response.- Returns:
- an
intspecifying the column index ofxcontaining the constant to be added to the linear response.
-
getConvergenceTol
public double getConvergenceTol()
Returns the convergence tolerance used.- Returns:
- a
doublespecifying the convergence tolerance used.
-
getFrequencyColumn
public int getFrequencyColumn()
Returns the column index ofxcontaining the frequency of response for each observation.- Returns:
- an
intspecifying the column index ofxcontaining the frequency of response for each observation.
-
getGradient
public double[] getGradient() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the inverse of the Hessian times the gradient vector, computed at the initial estimates.Note that the
setHessianOptionmethod must be invoked withwantHessianset totrueand thesetInitialEstimatesmethod must be invoked prior to invoking this method. Otherwise, the method throws anIllegalStateExceptionexception.- Returns:
- a
doublearray containing the inverse of the Hessian times the gradient vector, computed at the initial estimates. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getHessian
public double[][] getHessian() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the inverse of the Hessian of the negative of the log-likelihood, computed at the initial estimates.Note that the
Otherwise, the method throws ansetHessianOptionmethod must be invoked withwantHessianset totrueand thesetInitialEstimatesmethod must be invoked prior to invoking this method.IllegalStateExceptionexception.- Returns:
- a
doublematrix containing the inverse of the Hessian of the negative of the log-likelihood, computed at the initial estimates. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getHessianOption
public boolean getHessianOption()
Returns thebooleanused to indicate whether or not to compute the Hessian and gradient at the initial estimates.- Returns:
- a
booleanspecifying whether or not the Hessian and gradient are to be computed at the initial estimates. A return value equal totrueindicates that the Hessian and gradient are to be computed.
-
getInitialEstimates
public double[] getInitialEstimates() throws ProportionalHazards.ClassificationVariableLimitExceptionGets the initial parameter estimates.- Returns:
- a
doublearray containing the initial parameter estimates. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getLastUpdates
public double[] getLastUpdates() throws ProportionalHazards.ClassificationVariableLimitExceptionGets the last parameter updates.- Returns:
- a
doublearray containing the last parameter updates (excluding step halvings). - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getLogger
public Logger getLogger()
Returns the logger object and enables logging.- Returns:
- a
java.util.logging.Loggerobject, if present, ornull.
-
getMaxClass
public int getMaxClass()
Returns the upper bound used on the sum of the number of distinct values found among the classification variables inx.- Returns:
- an
intrepresenting the upper bound used on the sum of the number of distinct values found among the classification variables inx.
-
getMaximumLikelihood
public double getMaximumLikelihood() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the maximized log-likelihood.The log-likelihood is fully described in the
ProportionalHazardsclass description.- Returns:
- a
doublerepresenting the maximized log-likelihood - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getMaxIterations
public int getMaxIterations()
Return the maximum number of iterations allowed.- Returns:
- an
intspecifying the maximum number of iterations allowed.
-
getMeans
public double[] getMeans() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the means of the design variables.- Returns:
- a
doublearray containing the means of the design variables. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getNumberOfCoefficients
public int getNumberOfCoefficients() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the number of estimated coefficients in the model.- Returns:
- an
intscalar representing the number of estimated coefficients in the model. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getNumberRowsMissing
public int getNumberRowsMissing() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the number of rows of data inxthat contain missing values in one or more specific columns ofx.- Returns:
- an
intscalar representing the number of rows of data inxthat contain missing values in one or more specific columns ofx. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getParameterStatistics
public double[][] getParameterStatistics() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the parameter estimates and associated statistics.There is one row for each coefficient, and the columns of the returned matrix contain the following:
Column Statistic 0The coefficient estimate, 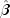
1Estimated standard deviation of the estimated coefficient 2Asymptotic normal score for testing that the coefficient is zero against the two-sided alternative 3p-value associated with the normal score in column 2 - Returns:
- a
doublematrix containing the parameter estimates and associated statistics. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getResponseColumn
public int getResponseColumn()
Returns the column index ofxcontaining the response time for each observation.- Returns:
- an
intspecifying the column index ofxcontaining the response time for each observation.
-
getStratumColumn
public int getStratumColumn()
Returns the column index ofxcontaining the stratum number for each observation.- Returns:
- an
intspecifying the column index ofxcontaining the stratum number for each observation.
-
getStratumNumbers
public int[] getStratumNumbers() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the stratum number used for each observation. IfstratumRatiois not -1.0, additional "strata" (other than those specified by columngroupIndexofxset via thesetStratumColumnmethod) may be generated. The array also contains a record of the generated strata. See theProportionalHazardsclass description for more detail.- Returns:
- an
intarray containing the stratum number used for each observation. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
getStratumRatio
public double getStratumRatio()
Returns the ratio at which a stratum is split into two strata.- Returns:
- a
doublespecifying the ratio at which a stratum is split into two strata.
-
getTiesOption
public int getTiesOption()
Returns the method used for handling ties.- Returns:
- an
intspecifying the method to be used in handling ties as indicated by the value in the following table:ValueMethod BRESLOWS_APPROXIMATEBreslow's approximate method. This is the default. SORTED_AS_PER_OBSERVATIONSFailures are assumed to occur in the same order as the observations input in x. The observations inxmust be sorted from largest to smallest failure time within each stratum, and grouped by stratum. All observations are treated as if their failure/censoring times were distinct when computing the log-likelihood.
-
getVarianceCovarianceMatrix
public double[][] getVarianceCovarianceMatrix() throws ProportionalHazards.ClassificationVariableLimitExceptionReturns the estimated asymptotic variance-covariance matrix of the parameters.- Returns:
- a
doublematrix containing the estimated asymptotic variance-covariance matrix of the parameters. - Throws:
ProportionalHazards.ClassificationVariableLimitException- is thrown if the classification variable limit set by the user throughsetUpperBoundhas been exceeded.
-
setCensorColumn
public void setCensorColumn(int censorIndex)
Sets the column index ofxcontaining the optional censoring code for each observation.If
x[i][censorIndex]equals 0, the failure timex[i][responseIndex]is treated as an exact time of failure. Otherwise, it is treated as right-censored time. By default, it is assumed that there is no censor code column inxand all observations are assumed to be exact failure times.- Parameters:
censorIndex- anintspecifying the column index ofxcontaining the optional censoring code for each observation.
-
setClassVarColumns
public void setClassVarColumns(int[] classVarIndices)
Sets the column indices ofxthat are the classification variables.- Parameters:
classVarIndices- anintarray containing the column numbers ofxthat are the classification variables. By default it is assumed there are no classification variables.
-
setConstantColumn
public void setConstantColumn(int fixedIndex)
Sets the column index ofxcontaining the constant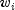 to be added
to the linear response.
to be added
to the linear response.
The linear response is taken to be
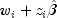 where
where 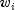 is the observation
constant,
is the observation
constant, 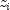 is the observation
design row vector, and
is the observation
design row vector, and  is the vector of estimated parameters. The "fixed"
constant allows one to test hypotheses about parameters
via the log-likelihoods.
If this method is not called, it is assumed that
is the vector of estimated parameters. The "fixed"
constant allows one to test hypotheses about parameters
via the log-likelihoods.
If this method is not called, it is assumed that
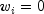 for all observations.
for all observations.- Parameters:
fixedIndex- anintspecifying the column index ofxcontaining the constant to be added to the linear response.
-
setConvergenceTol
public void setConvergenceTol(double convergenceTol)
Set the convergence tolerance.Convergence is assumed when the relative change in the maximum likelihood from one iteration to the next is less than
convergenceTol. IfconvergenceTolis zero,convergenceTol= 0.0001 is assumed. The default value is 0.0001.- Parameters:
convergenceTol- adoublespecifying the convergence tolerance.
-
setFrequencyColumn
public void setFrequencyColumn(int frequencyIndex)
Sets the column index ofxcontaining the frequency of response for each observation.By default it is assumed that there is no frequency response column recorded in
x. Each observation in the data array is assumed to be for a single failure; that is, the frequency of response for each observation is 1.- Parameters:
frequencyIndex- anintspecifying the column index ofxcontaining the frequency of response for each observation.
-
setHessianOption
public void setHessianOption(boolean wantHessian)
Set the option to have the Hessian and gradient be computed at the initial estimates.- Parameters:
wantHessian- abooleanspecifying whether or not the Hessian and gradient are to be computed at the initial estimates. If this option is set totruethe user must set the initial estimates via thesetInitialEstimatesmethod. By default the Hessian and gradient are not computed at the initial estimates.
-
setInitialEstimates
public void setInitialEstimates(double[] initialCoef)
Sets the initial parameter estimates.Care should be taken to ensure that the supplied estimates for the model coefficients
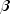 correspond to the generated
covariate vector
correspond to the generated
covariate vector 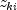 .
.- Parameters:
initialCoef- adoublearray containing the initial parameter estimates. By default the initial parameter estimates are all 0.0.
-
setMaxClass
public void setMaxClass(int maxClass)
Sets an upper bound on the sum of the number of distinct values found among the classification variables inx.For example, if the model consisted of of two class variables, one with the values {1, 2, 3, 4} and a second with the values {0, 1}, then the total number of different classification values is 4 + 2 = 6, and
maxClass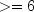 .
The default value is the number of observations
in
.
The default value is the number of observations
in x.- Parameters:
maxClass- anintrepresenting an upper bound on the sum of the number of distinct values found among the classification variables inx.
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Set the maximum number of iterations allowed.- Parameters:
maxIterations- anintspecifying the maximum number of iterations allowed. The default value is 30.
-
setResponseColumn
public void setResponseColumn(int responseIndex)
Sets the column index ofxcontaining the response variable.For point observations,
x[i][responseIndex]contains the time of the i-th event. For right-censored observations,x[i][responseIndex]contains the right-censoring time. Note that becauseProportionalHazardsonly uses the order of the events, negative "times" are allowed. By defaultresponseIndex = 0.- Parameters:
responseIndex- anintspecifying the column index ofxcontaining the response variable.
-
setStratumColumn
public void setStratumColumn(int stratumIndex)
Sets the column index ofxcontaining the stratification variable.Column
stratumIndexofxcontains a unique value for each stratum in the data. The risk set for an observation is determined by its stratum. By default it is assumed that all obvservations are from one statum.- Parameters:
stratumIndex- anintspecifying the column index ofxcontaining the stratification variable.
-
setStratumRatio
public void setStratumRatio(double stratumRatio)
Set the ratio at which a stratum is split into two strata.Let
be the observation proportionality constant, where
 is the design row vector for the k-th observation
and
is the design row vector for the k-th observation
and 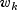 is the optional fixed
parameter specified by
is the optional fixed
parameter specified by 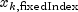 .
Let
.
Let 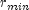 be the minimum value
be the minimum value
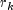 in a
stratum, where, for failed observations, the minimum is
over all times less than or equal to the time of occurrence
of the k-th observation. Let
in a
stratum, where, for failed observations, the minimum is
over all times less than or equal to the time of occurrence
of the k-th observation. Let 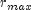 be the maximum value of
be the maximum value of 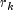 for the
remaining observations in the group. Then, if
for the
remaining observations in the group. Then, if 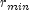
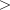
stratumRatio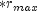 ,
the observations in the group are divided into two groups
at k. The default value of
,
the observations in the group are divided into two groups
at k. The default value of
stratumRatio= 1000 is usually good.Set
stratumRatioto any negative value if no division into strata is to be made.- Parameters:
stratumRatio- adoublespecifying the ratio at which a stratum is split into two strata.
-
setTiesOption
public void setTiesOption(int iTie)
Sets the method for handling ties.- Parameters:
iTie- anintspecifying the method to be used in handling ties. It can be eitherBRESLOWS_APPROXIMATEorSORTED_AS_PER_OBSERVATIONS.iTieMethod BRESLOWS_APPROXIMATEBreslow's approximate method. This is the default. SORTED_AS_PER_OBSERVATIONSFailures are assumed to occur in the same order as the observations input in x. The observations inxmust be sorted from largest to smallest failure time within each stratum, and grouped by stratum. All observations are treated as if their failure/censoring times were distinct when computing the log-likelihood.By default,
iTieisBRESLOWS_APPROXIMATE.
-
-