- java.lang.Object
-
- com.imsl.stat.Ranks
-
public class Ranks extends Object
Compute the ranks, normal scores, or exponential scores for a vector of observations.The class Ranks can be used to compute the ranks, normal scores, or exponential scores of the data in X. Ties in the data can be resolved in four different ways, as specified by member function
setTieBreaker. The type of values returned can vary depending on the member function called:GetRanks: Ordinary Ranks
For this member function, the values output are the ordinary ranks of the data in X. If X[i] has the smallest value among those in X and there is no other element in X with this value, then
getRanks(i)= 1. If both X[i] and X[j] have the same smallest value, thenif TieBreaker = 0, Ranks[i] =
getRanks([j]= 1.5
if TieBreaker = 1, Ranks[i] = Ranks[j] = 2.0
if TieBreaker = 2, Ranks[i] = Ranks[j] = 1.0
if TieBreaker = 3, Ranks[i] = 1.0 and Ranks[j] = 2.0
or Ranks[i] = 2.0 and Ranks[j] = 1.0.When the ties are resolved by use of function
setRandom, different results may occur when running the same program at different times unless the "seed" of the random number generator is set explicitly by use ofRandommethodsetSeed. Ordinarily, there is no need to call the routine to set the seed, even if there are ties in the data.getBlomScores: Normal Scores, Blom Version
Normal scores are expected values, or approximations to the expected values, of order statistics from a normal distribution. The simplest approximations are obtained by evaluating the inverse cumulative normal distribution function,
inverseNormal, at the ranks scaled into the open interval (0, 1). In the Blom version (see Blom 1958), the scaling transformation for the rank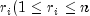 , where n is
the sample size is
, where n is
the sample size is 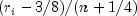 .
The Blom normal score corresponding to the observation with rank
.
The Blom normal score corresponding to the observation with rank
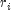 is
is
where
 is the normal cumulative
distribution function.
is the normal cumulative
distribution function.Adjustments for ties are made after the normal score transformation. That is, if X[i] equals X[j] (within fuzz) and their value is the k-th smallest in the data set, the Blom normal scores are determined for ranks of k and k + 1, and then these normal scores are averaged or selected in the manner specified by TieBreaker, which is set by the method
setTieBreaker. (Whether the transformations are made first or ties are resolved first makes no difference except when averaging is done.)getTukeyScores: Normal Scores, Tukey Version
In the Tukey version (see Tukey 1962), the scaling transformation for the rank
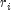 is
is 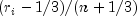 .
The Tukey normal score corresponding to the observation with rank
.
The Tukey normal score corresponding to the observation with rank
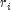 is
is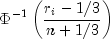
Ties are handled in the same way as discussed above for the Blom normal scores.
getVanDerWaerdenScores: Normal Scores, Van der Waerden Version
In the Van der Waerden version (see Lehmann 1975, page 97), the scaling transformation for the rank
 is
is
 . The Van der Waerden normal score
corresponding to the observation with rank
. The Van der Waerden normal score
corresponding to the observation with rank 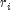 is
is 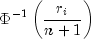
Ties are handled in the same way as discussed above for the Blom normal scores.
getNormalScores: Expected Value of Normal Order Statistics
The method
getNormalScoresreturns the expected values of the normal order statistics. If the value in X[i] is the k-th smallest, then the valuegetNormalScores[i]is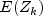 , where
, where  is the
expectation operator and
is the
expectation operator and 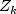 is the k-th order
statistic in a sample of size
is the k-th order
statistic in a sample of size NOBSfrom a standard normal distribution. Ties are handled in the same way as discussed above for the Blom normal scores.getSavageScores: Savage Scores
The method
getSavageScoresreturns the expected values of the exponential order statistics. These values are called Savage scores because of their use in a test discussed by Savage (1956) (see Lehman 1975). If the value in X[i] is the k-th smallest, then the i-th output value output is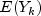 , where
, where
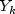 is the k-th order statistic in a sample of
size n from a standard exponential distribution. The
expected value of the k-th order statistic from an exponential sample
of size n is
is the k-th order statistic in a sample of
size n from a standard exponential distribution. The
expected value of the k-th order statistic from an exponential sample
of size n is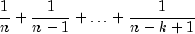
Ties are handled in the same way as discussed above for the Blom normal scores.
- See Also:
- Example
-
-
Field Summary
Fields Modifier and Type Field and Description static intTIE_AVERAGEIn case of ties, use the average of the scores of the tied observations.static intTIE_HIGHESTIn case of ties, use the highest score in the group of ties.static intTIE_LOWESTIn case of ties, use the lowest score in the group of ties.static intTIE_RANDOMIn case of ties, use one of the group of ties chosen at random.
-
Constructor Summary
Constructors Constructor and Description Ranks()Constructor for the Ranks class.
-
Method Summary
Methods Modifier and Type Method and Description static doubleexpectedNormalOrderStatistic(int i, int n)Returns the expected value of a normal order statistic.double[]getBlomScores(double[] x)Gets the Blom version of normal scores for each observation.double[]getNormalScores(double[] x)Gets the expected value of normal order statistics (for tied observations, the average of the expected normal scores).double[]getRanks(double[] x)Gets the rank for each observation.double[]getSavageScores(double[] x)Gets the Savage scores (the expected value of exponential order statistics).double[]getTukeyScores(double[] x)Gets the Tukey version of normal scores for each observation.double[]getVanDerWaerdenScores(double[] x)Gets the Van der Waerden version of normal scores for each observation.voidsetFuzz(double fuzz)Sets the fuzz factor used in determining ties.voidsetRandom(Random random)Sets theRandomobject.voidsetTieBreaker(int iTie)Sets the tie breaker for Ranks.
-
-
-
Field Detail
-
TIE_AVERAGE
public static final int TIE_AVERAGE
In case of ties, use the average of the scores of the tied observations.- See Also:
- Constant Field Values
-
TIE_HIGHEST
public static final int TIE_HIGHEST
In case of ties, use the highest score in the group of ties.- See Also:
- Constant Field Values
-
TIE_LOWEST
public static final int TIE_LOWEST
In case of ties, use the lowest score in the group of ties.- See Also:
- Constant Field Values
-
TIE_RANDOM
public static final int TIE_RANDOM
In case of ties, use one of the group of ties chosen at random.- See Also:
- Constant Field Values
-
-
Method Detail
-
expectedNormalOrderStatistic
public static double expectedNormalOrderStatistic(int i, int n)Returns the expected value of a normal order statistic.- Parameters:
i- anint, the rank of the order statisticn- anint, the sample size- Returns:
- a
double, the expected value of the i-th order statistic in a sample of size n from the standard normal distribution
-
getBlomScores
public double[] getBlomScores(double[] x)
Gets the Blom version of normal scores for each observation.- Parameters:
x- adoublearray which contains the observations to be ranked- Returns:
- a
doublearray which contains the Blom version of normal scores for each observation in x
-
getNormalScores
public double[] getNormalScores(double[] x)
Gets the expected value of normal order statistics (for tied observations, the average of the expected normal scores).- Parameters:
x- adoublearray which contains the observations- Returns:
- a
doublearray which contains the expected value of normal order statistics for the observations in x (for tied observations, the average of the expected normal scores)
-
getRanks
public double[] getRanks(double[] x)
Gets the rank for each observation.- Parameters:
x- adoublearray which contains the observations to be ranked- Returns:
- a
doublearray which contains the rank for each observation in x
-
getSavageScores
public double[] getSavageScores(double[] x)
Gets the Savage scores (the expected value of exponential order statistics).- Parameters:
x- adoublearray which contains the observations- Returns:
- a
doublearray which contains the Savage scores for the observations in x. (the expected value of exponential order statistics)
-
getTukeyScores
public double[] getTukeyScores(double[] x)
Gets the Tukey version of normal scores for each observation.- Parameters:
x- adoublearray which contains the observations to be ranked- Returns:
- a
doublearray which contains the Tukey version of normal scores for each observation in x
-
getVanDerWaerdenScores
public double[] getVanDerWaerdenScores(double[] x)
Gets the Van der Waerden version of normal scores for each observation.- Parameters:
x- adoublearray which contains the observations to be ranked- Returns:
- a
doublearray which contains the Van der Waerden version of normal scores for each observation in x
-
setFuzz
public void setFuzz(double fuzz)
Sets the fuzz factor used in determining ties.- Parameters:
fuzz- adoublewhich represents the fuzz factor
-
setRandom
public void setRandom(Random random)
Sets theRandomobject.- Parameters:
random- aRandomobject used in breaking ties
-
setTieBreaker
public void setTieBreaker(int iTie)
Sets the tie breaker for Ranks.- Parameters:
iTie- anintwhich represents the tie breaker
-
-