- java.lang.Object
-
- com.imsl.stat.Sort
-
public class Sort extends Object
A collection of sorting functions.Class
Sortcontains ascending and descending methods for sorting elements of an array or a matrix.The QuickSort algorithm is used, except for short sequences that are handled using an insertion sort.
The QuickSort algorithm is a randomized QuickSort with 3-way partitioning. Basic QuickSort is slow if the sequence to be sorted contains many duplicate keys. The 3-way partitioning algorithm eliminates this problem. The pivot is chosen as the middle element of three potential pivots chosen at random.
The matrix ascending method sorts the rows of real matrix
xusing a particular column or columns inxas the keys. The sort is algebraic with the first key as the most significant, the second key as the next most significant, etc. When x is sorted in ascending order, the resulting sorted array is such that the following is true:- For
![i=0,1,ldots,{rm nObs}-2,{rm x}[i][{rm indKeys},,
[0]]leq{rm x}[i + 1][{rm indKeys}[0]], mbox{where nObs is the number of
observations.}](eqn_2093.png)
- For
![k=1,ldots,{rm nKeys-1,if,,x[i][{rm indKeys}[j]]=
x[i+1][{rm indKeys}[j]]}](eqn_2094.png) for
for 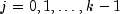 , then
, then ![{rm x}[i][{rm indKeys}[k]]={rm x}[i+1][{rm
indKeys}[k]]](eqn_2096.png)
The observations also can be sorted in descending order.
The rows ofxcontaining the missing value code NaN in at least one of the specified columns are considered as an additional group. These rows are moved to the end of the sortedx.If all of the sort keys in a pair of rows are equal then the rows keep their original relative order.
The sorting algorithm is based on a quicksort method given by Singleton (1969) with modifications, see Bentley and Sedgewick (1997).
- For
-
-
Method Summary
Methods Modifier and Type Method and Description static voidascending(double[] ra)Sorts an array into ascending order.static voidascending(double[][] ra, int nKeys)Sorts a matrix into ascending order by the firstnKeys.static voidascending(double[][] ra, int[] indKeys)Sorts a matrix into ascending order by specified keys.static voidascending(double[][] ra, int[] indKeys, int[] iPerm)Sorts a matrix into ascending order by specified keys and returns the permutation vector.static voidascending(double[][] ra, int nKeys, int[] iPerm)Sorts a matrix into ascending order according to the firstnKeyskeys and returns the permutation vector.static voidascending(double[] ra, int[] iPerm)Sorts an array into ascending order and returns the permutation vector.static voidascending(int[] ia)Sorts an integer array into ascending order.static voidascending(int[][] ia, int nKeys)Sorts a matrix into ascending order by the firstnKeys.static voidascending(int[][] ia, int[] indKeys, int[] iPerm)Sorts a matrix into ascending order by specified keys and returns the permutation vector.static voidascending(int[][] ia, int nKeys, int[] iPerm)Sorts a matrix into ascending order according to the firstnKeyskeys and returns the permutation vector.static voidascending(int[] ia, int[] iPerm)Sorts an integer array into ascending order and returns the permutation vector.static voiddescending(double[] ra)Sorts an array into descending order.static voiddescending(double[][] ra, int nKeys)Sorts a matrix into descending order by the firstnkeys.static voiddescending(double[][] ra, int[] indKeys)Sorts a matrix into descending order by specified keys.static voiddescending(double[][] ra, int[] indKeys, int[] iPerm)Sorts a matrix into descending order by specified keys and return the permutation vector.static voiddescending(double[][] ra, int nKeys, int[] iPerm)Sorts a matrix into descending order by the firstnkeysand returns the permutation vector.static voiddescending(double[] ra, int[] iPerm)Sorts an array into descending order and returns the permutation vector.static voiddescending(int[] ra)Sorts an integer array into descending order.static voiddescending(int[] ra, int[] iPerm)Sorts an integer array into descending order and returns the permutation vector.
-
-
-
Method Detail
-
ascending
public static void ascending(double[] ra)
Sorts an array into ascending order.- Parameters:
ra- adoublearray to be sorted into ascending order
-
ascending
public static void ascending(double[][] ra, int nKeys)Sorts a matrix into ascending order by the firstnKeys.- Parameters:
ra- adoublematrix to be sorted into ascending ordernKeys- anint, the number of keys. The firstnKeyscolumns ofraare to be used as the sorting keys.
-
ascending
public static void ascending(double[][] ra, int[] indKeys)Sorts a matrix into ascending order by specified keys.- Parameters:
ra- adoublematrix to be sorted into ascending orderindKeys- anintarray containing the order into which the columns ofraare to be sorted. These values must be between 0 and one less than the number of columns inra.
-
ascending
public static void ascending(double[][] ra, int[] indKeys, int[] iPerm)Sorts a matrix into ascending order by specified keys and returns the permutation vector.- Parameters:
ra- adoublematrix to be sorted into ascending orderindKeys- anintarray containing the order into which the columns ofraare to be sorted. These values must be between 0 and one less than the number of columns inra.iPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
ascending
public static void ascending(double[][] ra, int nKeys, int[] iPerm)Sorts a matrix into ascending order according to the firstnKeyskeys and returns the permutation vector.- Parameters:
ra- adoublematrix to be sorted into ascending ordernKeys- anint, the number of keys. The firstnKeyscolumns ofraare to be used as the sorting keys.iPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
ascending
public static void ascending(double[] ra, int[] iPerm)Sorts an array into ascending order and returns the permutation vector.- Parameters:
ra- adoublearray to be sorted into ascending orderiPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
ascending
public static void ascending(int[] ia)
Sorts an integer array into ascending order.- Parameters:
ia- anintarray to be sorted into ascending order
-
ascending
public static void ascending(int[][] ia, int nKeys)Sorts a matrix into ascending order by the firstnKeys.- Parameters:
ia- anintmatrix to be sorted into ascending ordernKeys- anint, the number of keys. The firstnKeyscolumns ofiaare to be used as the sorting keys.
-
ascending
public static void ascending(int[][] ia, int[] indKeys, int[] iPerm)Sorts a matrix into ascending order by specified keys and returns the permutation vector.- Parameters:
ia- anintmatrix to be sorted into ascending orderindKeys- anintarray containing the order into which the columns ofiaare to be sorted. These values must be between 0 and one less than the number of columns inia.iPerm- anintarray that on input is the same length asiaand contains the values 0, 1, .... On output, the values represent the permutation of the values inia, that is, the re-ordering of those values in terms of their previous position.
-
ascending
public static void ascending(int[][] ia, int nKeys, int[] iPerm)Sorts a matrix into ascending order according to the firstnKeyskeys and returns the permutation vector.- Parameters:
ia- anintmatrix to be sorted into ascending ordernKeys- anint, the number of keys. The firstnKeyscolumns ofiaare to be used as the sorting keys.iPerm- anintarray that on input is the same length asiaand contains the values 0, 1, .... On output, the values represent the permutation of the values inia, that is, the re-ordering of those values in terms of their previous position.
-
ascending
public static void ascending(int[] ia, int[] iPerm)Sorts an integer array into ascending order and returns the permutation vector.- Parameters:
ia- anintarray to be sorted into ascending orderiPerm- anintarray that on input is the same length asiaand contains the values 0, 1, .... On output, the values represent the permutation of the values inia, that is, the re-ordering of those values in terms of their previous position.
-
descending
public static void descending(double[] ra)
Sorts an array into descending order.- Parameters:
ra- adoublearray to be sorted into descending order
-
descending
public static void descending(double[][] ra, int nKeys)Sorts a matrix into descending order by the firstnkeys.- Parameters:
ra- adoublematrix to be sorted into descending ordernKeys- anint, the number of keys. The firstnKeyscolumns ofraare to be used as the sorting keys.
-
descending
public static void descending(double[][] ra, int[] indKeys)Sorts a matrix into descending order by specified keys.- Parameters:
ra- adoublematrix to be sorted into descending orderindKeys- anintarray containing the order into which the columns ofraare to be sorted. These values must be between 0 and one less than the number of columns inra.
-
descending
public static void descending(double[][] ra, int[] indKeys, int[] iPerm)Sorts a matrix into descending order by specified keys and return the permutation vector.- Parameters:
ra- adoublematrix to be sorted into descending orderindKeys- anintarray containing the order into which the columns ofraare to be sorted. These values must be between 0 and one less than the number of columns inra.iPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
descending
public static void descending(double[][] ra, int nKeys, int[] iPerm)Sorts a matrix into descending order by the firstnkeysand returns the permutation vector.- Parameters:
ra- adoublematrix to be sorted into descending ordernKeys- anint, the number of keys. The firstnKeyscolumns ofraare to be used as the sorting keys.iPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
descending
public static void descending(double[] ra, int[] iPerm)Sorts an array into descending order and returns the permutation vector.- Parameters:
ra- adoublearray to be sorted into descending orderiPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
descending
public static void descending(int[] ra)
Sorts an integer array into descending order.- Parameters:
ra- anintarray to be sorted into descending order
-
descending
public static void descending(int[] ra, int[] iPerm)Sorts an integer array into descending order and returns the permutation vector.- Parameters:
ra- anintarray to be sorted into descending orderiPerm- anintarray that on input is the same length asraand contains the values 0, 1, .... On output, the values represent the permutation of the values inra, that is, the re-ordering of those values in terms of their previous position.
-
-