Package com.imsl.stat

Class Cdf

java.lang.Object
com.imsl.stat.Cdf
public final class Cdf extends Object
Cumulative probability distribution functions.
See Also:

  • Method Details

    • binomial

      public static double binomial(int k, int n, double pin)
      Evaluates the binomial cumulative probability distribution function.

      Method binomial evaluates the distribution function of a binomial random variable with parameters n and p with p=pin. It does this by summing probabilities of the random variable taking on the specific values in its range. These probabilities are computed by the recursive relationship

      $$\Pr \left( {X = j} \right) = \frac{{\left( {n + 1 - j} \right)p}}{{j\left( {1 - p} \right)}}\Pr \left( {X = j - 1} \right)$$

      To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than n times p, and are computed backward from n, otherwise. The smallest positive machine number, \(\varepsilon\), is used as the starting value for summing the probabilities, which are rescaled by \((1 - p)^n\varepsilon\) if forward computation is performed and by \(p^n\varepsilon\) if backward computation is done. For the special case of p = 0, binomial is set to 1; and for the case p = 1, binomial is set to 1 if k = n and to 0 otherwise.

      Parameters:
      k - the int argument for which the binomial distribution function is to be evaluated.
      n - the int number of Bernoulli trials.
      pin - a double, the probability of success on each independent trial.
      Returns:
      a double, the probability that a binomial random variable takes a value less than or equal to k. This value is the probability that k or fewer successes occur in n independent Bernoulli trials, each of which has a pin probability of success.
      See Also:

    • bivariateNormal

      public static double bivariateNormal(double x, double y, double rho)
      Evaluates the bivariate normal cumulative probability distribution function. Let \((X,Y)\) be a bivariate normal variable with mean \((0,0)\) and variance-covariance matrix $$ \left[ \begin{array}{cc} 1 & \rho \\ \rho & 1\end{array}\right] $$ This method computes the probability that \(X \le {\tt x}\) and \(Y \le {\tt y}\).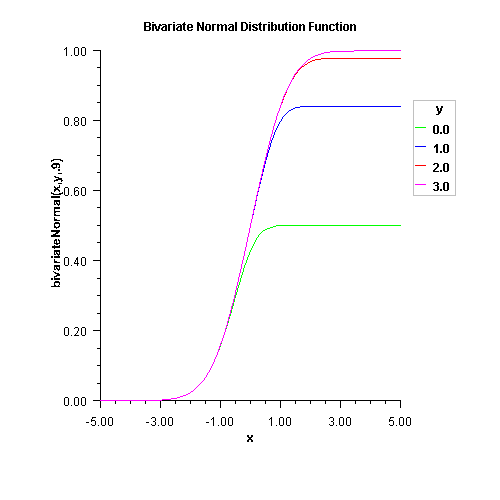

      Plot of Bivariate Normal Distribution Function

      Parameters:
      x - is the x-coordinate of the point for which the bivariate normal distribution function is to be evaluated.
      y - is the y-coordinate of the point for which the bivariate normal distribution function is to be evaluated.
      rho - is the correlation coefficient.
      Returns:
      the probability that a bivariate normal random variable \((X,Y)\) with correlation rho satisfies \(X \le {\tt x}\) and \(Y \le {\tt y}\).

    • poisson

      public static double poisson(int k, double theta)
      Evaluates the Poisson cumulative probability distribution function.

      poisson evaluates the distribution function of a Poisson random variable with parameter theta. theta, which is the mean of the Poisson random variable, must be positive. The probability function (with \(\theta = theta\)) is

      $$f(x) = e^{ - \theta } \theta ^x /x!\,\,\, for\,x = 0,\,1,\,2,\, \ldots $$

      The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed. poisson uses the recursive relationship

      $$f\left( {x + 1} \right) = f\left( x \right) (\theta /\left( {x + 1} \right)),\,\,\,for\,x = 0,\,1,\,2,\, \ldots k-1$$

      with \(f(0) = e^{-\theta}\).

      Parameters:
      k - the int argument for which the Poisson distribution function is to be evaluated
      theta - a double, the mean of the Poisson distribution
      Returns:
      a double, the probability that a Poisson random variable takes a value less than or equal to k
      See Also:

    • betaMean

      public static double betaMean(double pin, double qin)
      Evaluates the mean of the beta cumulative probability distribution function
      Parameters:
      pin - a double, the first beta distribution parameter.
      qin - a double, the second beta distribution parameter.
      Returns:
      a double, the mean of the beta distribution function.

    • betaVariance

      public static double betaVariance(double pin, double qin)
      Evaluates the variance of the beta cumulative probability distribution function
      Parameters:
      pin - a double, the first beta distribution parameter.
      qin - a double, the second beta distribution parameter.
      Returns:
      a double, the variance of the beta distribution function.

    • F

      public static double F(double x, double dfn, double dfd)
      Evaluates the F cumulative probability distribution function.

      F evaluates the distribution function of a Snedecor's F random variable with dfn numerator degrees of freedom and dfd denominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using the function beta. If X is an F variate with \(v_1\) and \(v_2\) degrees of freedom and \(Y = v_1X/(v_2 + v_1X)\), then Y is a beta variate with parameters \(p = v_1/2\) and \(q = v_2/2\). F also uses a relationship between F random variables that can be expressed as follows:

      $${\rm F}(X, {\it dfn}, {\it dfd})= {\rm F}(1/X, {\it dfd}, {\it dfn})$$

      For greater right tail accuracy, see complementaryF(double, double, double).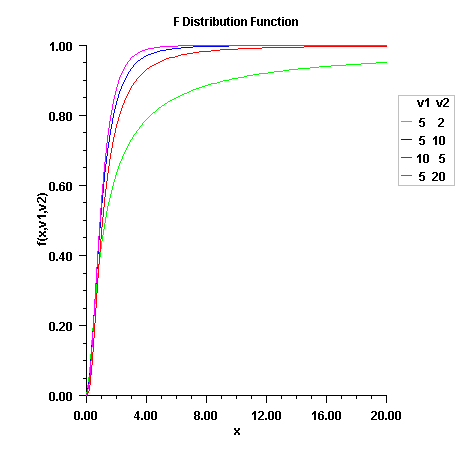

      Plot of F Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      dfn - a double, the numerator degrees of freedom. It must be positive.
      dfd - a double, the denominator degrees of freedom. It must be positive.
      Returns:
      a double, the probability that an F random variable takes on a value less than or equal to x.
      See Also:

    • complementaryF

      public static double complementaryF(double x, double dfn, double dfd)
      Calculates the complement of the F distribution function.

      complementaryF evaluates one minus the distribution function of a Snedecor's F random variable with dfn numerator degrees of freedom and dfd denominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using the function beta. If X is an F variate with \(v_1\) and \(v_2\) degrees of freedom and \(Y = v_1X/(v_2 + v_1X)\), then Y is a beta variate with parameters \(p = v_1/2\) and \(q = v_2/2\). complementaryF also uses a relationship between F random variables that can be expressed as follows:

      $${\rm F}(X, {\it dfn}, {\it dfd})= {\rm F}(1/X, {\it dfd}, {\it dfn})$$

      This function provides higher right tail accuracy for the F distribution.

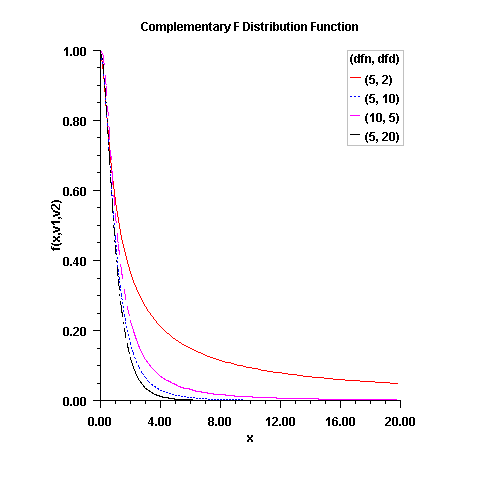
      Plot of F Distribution Function

      Parameters:
      x - a double, the argument at which \( Pr\left( x \gt F \right)\) is to be evaluated.
      dfn - a double, the numerator degrees of freedom. It must be positive.
      dfd - a double, the denominator degrees of freedom. It must be positive.
      Returns:
      a double, the probability that an F random variable takes on a value greater than x.

    • complementaryF2

      public static double complementaryF2(double x, double dfn, double dfd)

    • hypergeometric

      public static double hypergeometric(int k, int sampleSize, int defectivesInLot, int lotSize)
      Evaluates the hypergeometric cumulative probability distribution function.

      Method hypergeometric evaluates the distribution function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable X can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is

      $$\Pr \left( {X = j} \right) = \frac{{\left( {_j^m } \right)\left( {_{n - j}^{l - m} } \right)}}{{\left( {_n^l } \right)}}{\rm{for }}\,\,j = i,\;i + 1,\,\,i + 2,\; \ldots ,\;\min \left( {n,m} \right)$$

      where \(i = {\rm max}(0, n - l + m)\).

      If k is greater than or equal to i and less than or equal to \(\min (n, m)\), hypergeometric sums the terms in this expression for j going from i up to k. Otherwise, hypergeometric returns 0 or 1, as appropriate. So, as to avoid rounding in the accumulation, hypergeometric performs the summation differently depending on whether or not k is greater than the mode of the distribution, which is the greatest integer less than or equal to \((m + 1)(n + 1)/(l + 2)\).

      Parameters:
      k - an int, the argument at which the function is to be evaluated.
      sampleSize - an int, the sample size, n.
      defectivesInLot - an int, the number of defectives in the lot, m.
      lotSize - an int, the lot size, l.
      Returns:
      a double, the probability that a hypergeometric random variable takes a value less than or equal to k.
      See Also:

    • gamma

      public static double gamma(double x, double a)
      Evaluates the gamma cumulative probability distribution function.

      Method gamma evaluates the distribution function, F, of a gamma random variable with shape parameter a; that is,

      $$F\left( x \right) = \frac{1}{{\Gamma \left( a \right)}}\int_0^x {e^{ - t} t^{a - 1} } dt $$

      where \(\Gamma(\cdot)\) is the gamma function. (The gamma function is the integral from 0 to \(\infty\) of the same integrand as above). The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

      The gamma distribution is often defined as a two-parameter distribution with a scale parameter b (which must be positive), or even as a three-parameter distribution in which the third parameter c is a location parameter. In the most general case, the probability density function over \((c, \infty)\) is

      $$f\left( t \right) = \frac{1}{{b^a \Gamma \left( a \right)}}e^{ - \left( {t - c} \right)/b} \left( {x - c} \right)^{a - 1}$$

      If T is such a random variable with parameters a, b, and c, the probability that \(T \le t_0\) can be obtained from gamma by setting \(X = (t_0 - c)/b\).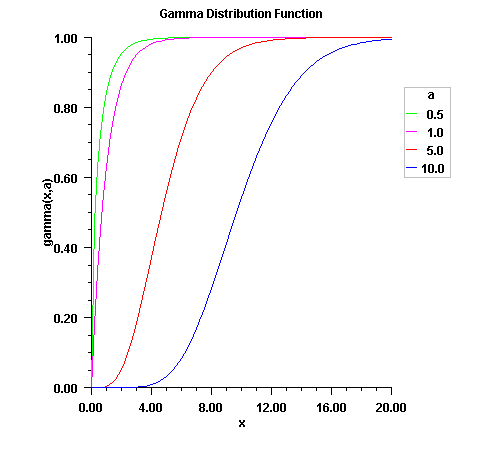

      Gamma Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      a - a double, the shape parameter. This must be positive.
      Returns:
      a double,the probability that a gamma random variable takes on a value less than or equal to x
      See Also:

    • exponential

      public static double exponential(double x, double scale)
      Evaluates the exponential cumulative probability distribution function.

      Method exponential is a special case of the gamma distribution function, which evaluates the distribution function, F, with scale parameter b and shape parameter a, used in the gamma distribution function equal to 1.0. That is,

      $$F\left( x \right) = \frac{1}{{\Gamma \left( a \right)}}\int_0^x {e^{ - t/b}} dt$$

      where \(\Gamma(\cdot)\) is the gamma function. (The gamma function is the integral from 0 to \(\infty\) of the same integrand as above). The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

      If x is less than or equal to 1.0, gamma uses a series expansion. Otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)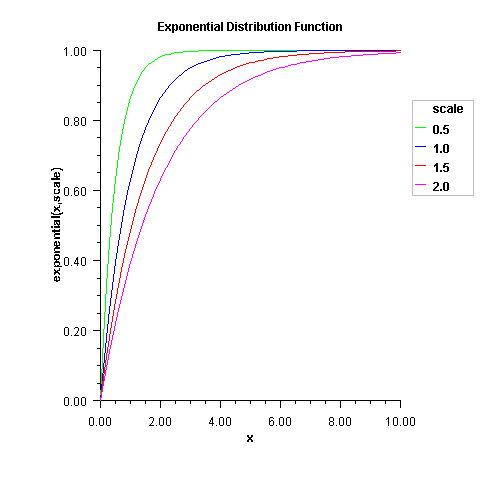

      Plot of Exponential Distribution Function

      Parameters:
      x - a double the argument at which the function is to be evaluated
      scale - a double, the scale parameter, \(b\)
      Returns:
      a double, the probability that an exponential random variable takes on a value less than or equal to x
      See Also:

    • normal

      public static double normal(double x)
      Evaluates the standard normal (Gaussian) cumulative probability distribution function.

      Method normal evaluates the distribution function, \(\Phi\), of a standard normal (Gaussian) random variable, that is,

      $$\Phi \left( x \right) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^x {} e^{ - t^2 /2} dt$$

      The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

      The standard normal distribution (for which normal is the distribution function) has mean of 0 and variance of 1. The probability that a normal random variable with mean \(\mu\) and variance \(\sigma^2\) is less than y is given by normal evaluated at \((y - \mu)/\sigma\).

      \(\Phi(x)\) is evaluated by use of the complementary error function, erfc. The relationship is:

      $$\Phi (x) = {\rm{erfc}}( - x/ \sqrt {2.0}) /2$$

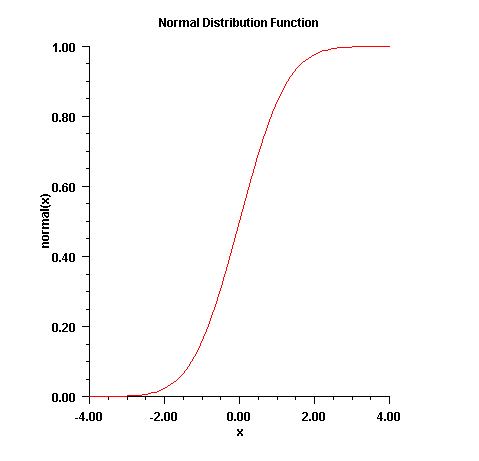
      Standard Normal Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      Returns:
      a double, the probability that a normal variable takes a value less than or equal to x
      See Also:

    • chiMean

      public static double chiMean(double df)
      Evaluates the mean of the chi-squared cumulative probability distribution function
      Parameters:
      df - a double, the number of degrees of freedom. This must be at least 0.5.
      Returns:
      a double, the mean of the chi-squared distribution function

    • chiVariance

      public static double chiVariance(double df)
      Evaluates the variance of the chi-squared cumulative probability distribution function
      Parameters:
      df - a double, the number of degrees of freedom. This must be at least 0.5.
      Returns:
      a double, the variance of the chi-squared distribution function

    • chi

      public static double chi(double chsq, double df)
      Evaluates the chi-squared cumulative distribution function.

      Method chi evaluates the cumulative distribution function (CDF) F, of a chi-squared random variable with df degrees of freedom, that is, with x = chsq and \(\nu\) = df,

      $$F\left( x, \nu \right) \;=\; \frac{1}{{2^{\nu /2} \Gamma \left( {\nu /2} \right)}} \int_0^x {e^{ - t/2} t^{\nu /2 - 1} } dt$$

      where \(\Gamma (\cdot)\) is the gamma function. The value \(p \;=\; F\left( x, \nu \right)\) is the probability that the random variable takes a value less than or equal to x.

      For \(\nu \;>\; 343\), chi uses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, equation 26.4.17) for p in terms of the normal CDF, which is evaluated using method normal.

      For \(\nu \;\le\; 343\), chi uses series expansions to evaluate p: for \(x \;\lt\; \nu\), chi calculates p using A&S equation 6.5.29, and for \(x \;\ge\; \nu\), chi calculates p using the continued fraction (CF) expansion of the incomplete gamma function given in A&S equation 6.5.31 and implemented using Lentz's algorithm (Lentz, W.J., 1976, Applied Optics, vol. 15, pp. 668-671) as modified by Thompson & Barnett (Thompson, I.J., and Barnett, A.R., 1986, Journal of Computational Physics, vol. 64, pp. 490-509).

      For greater right tail accuracy, see complementaryChi(double, double).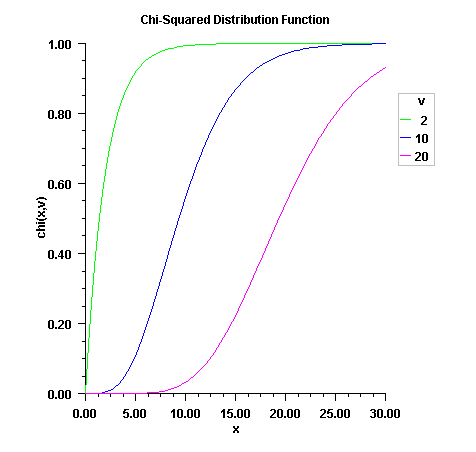

      Plot of Chi-Squared Distribution Function

      Parameters:
      chsq - a double, the argument at which the function is to be evaluated
      df - a double, the number of degrees of freedom. df must be positive.
      Returns:
      a double, the probability that a chi-squared random variable takes a value less than or equal to chsq
      See Also:

    • complementaryChi

      public static double complementaryChi(double chsq, double df)
      Calculates the complement of the chi-squared cumulative distribution function.

      Method complementaryChi evaluates the cumulative distribution function, \(1-F\), of a chi-squared random variable with df degrees of freedom, that is, with x = chsq and \(\nu\) = df,

      $$p \;=\; F\left( x, \nu \right) \;=\; \frac{1}{{2^{\nu /2} \Gamma \left( {\nu /2} \right)}} \int_0^x {e^{ - t/2} t^{\nu /2 - 1} } dt$$

      where \(\Gamma (\cdot)\) is the gamma function. The value of the complementaryChi distribution function at the point x, \(1 - p\), is the probability that the random variable takes a value greater than x.

      For \(\nu \;>\; 343\), complementaryChi uses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, equation 26.4.17) for p in terms of the normal CDF, which is evaluated using method normal.

      For \(\nu \;\le\; 343\), complementaryChi uses series expansions to evaluate p: for \(x \;\lt\; \nu\), complementaryChi calculates p using A&S series 6.5.29, and for \(x \;\ge\; \nu\), complementaryChi calculates p using the continued fraction expansion of the incomplete gamma function given in A&S equation 6.5.31 and implemented using Lentz's algorithm (Lentz, W.J., 1976, Applied Optics, vol. 15, pp. 668-671) as modified by Thompson & Barnett (Thompson, I.J., and Barnett, A.R., 1986, Journal of Computational Physics, vol. 64, pp. 490-509).

      complementaryChi provides greater right tail accuracy for the Chi-squared distribution than does 1 - chi.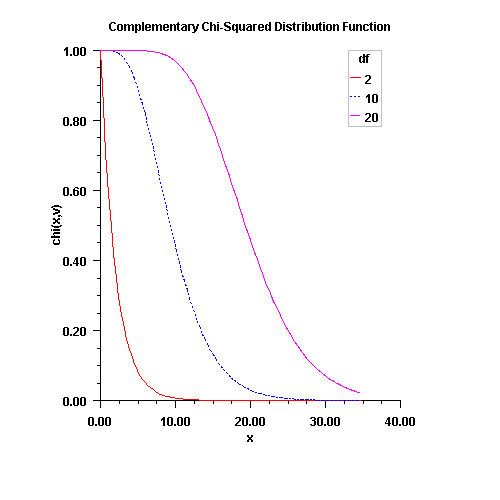

      Plot of Chi-Squared Distribution Function

      Parameters:
      chsq - a double, the value at which the function is to be evaluated
      df - a double, the number of degrees of freedom. df must be positive.
      Returns:
      a double, the probability that a chi-squared random variable takes a value greater than chsq

    • noncentralBeta

      public static double noncentralBeta(double x, double shape1, double shape2, double lambda)
      Evaluates the noncentral beta cumulative distribution function (CDF).

      The noncentral beta distribution is a generalization of the beta distribution. If \(Z\) is a noncentral chi-square random variable with noncentrality parameter \(\lambda\) and \(2 \alpha_1\) degrees of freedom, and \(Y\) is a chi-square random variable with \(2 \alpha_2\) degrees of freedom which is statistically independent of \(Z\), then

      $$X \;\; = \;\; \frac{Z}{Z \; + \; Y} \;\; = \;\; \frac{\alpha_1 F}{\alpha_1 F \; + \; \alpha_2}$$

      is a noncentral beta-distributed random variable and

      $$F \;\; = \;\; \frac{\alpha_2 Z}{\alpha_1 Y} \;\; = \;\; \frac{\alpha_2 X}{\alpha_1 (1 \; - \; X)}$$

      is a noncentral F-distributed random variable. The CDF for noncentral beta variable X can thus be simply defined in terms of the noncentral F CDF:

      $$CDF_{nc\beta}(x, \; \alpha_1, \; \alpha_2, \; \lambda) \;\; = \;\; CDF_{ncF}(f, \; 2 \alpha_1, \; 2 \alpha_2, \; \lambda)$$

      where \(CDF_{nc\beta}(x, \; \alpha_1, \; \alpha_2, \; \lambda)\) is the noncentral beta CDF with \(x\) = x, \(\alpha_1\) = shape1, \(\alpha_2\) = shape2, and noncentrality parameter \(\lambda\) = lambda; \(CDF_{ncF}(f, \; 2 \alpha_1, \; 2 \alpha_2, \; \lambda)\) is the noncentral F CDF with argument f, numerator and denominator degrees of freedom \(2 \alpha_1\) and \(2 \alpha_2\) respectively, and noncentrality parameter \(\lambda\); and:

      $$f \;\; = \;\; \frac{\alpha_2 x}{\alpha_1 (1 \; - \; x)}; \;\; x \;\; = \;\; \frac{\alpha_1 f}{\alpha_1 f \; + \; \alpha_2}$$

      (See documentation for class Cdf method noncentralF for a discussion of how the noncentral F CDF is defined and calculated.)

      With a noncentrality parameter of zero, the noncentral beta distribution is the same as the beta distribution.

      Parameters:
      x - a double, the argument at which the function is to be evaluated x must be nonnegative and less than or equal to 1.
      shape1 - a double, the first shape parameter. shape1 must be positive.
      shape2 - a double, the second shape parameter. shape2 must be positive.
      lambda - a double, the noncentrality parameter. lambda must nonnegative.
      Returns:
      a double, the probability that a noncentral beta random variable takes a value less than or equal to x

    • noncentralchi

      public static double noncentralchi(double chsq, double df, double alam)
      Evaluates the noncentral chi-squared cumulative probability distribution function.

      Method noncentralchi evaluates the distribution function, F, of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with \(\nu = {\rm df}\), \(\lambda = {\rm alam}\), and \(\chi = {\rm chsq}\),

      $$F\left( x \right) = \sum\limits_{i = 0}^\infty {\frac{e^{-\lambda/2}\left(\lambda/2\right)^i}{i!}} \int_0^x {\frac{t^{\left(\nu + 2i\right)/2-1}e^{ - t/2}} {2^{\left(\nu+2i\right)/2}{\Gamma\left(\frac{\nu+2i}{2}\right)}}} dt$$

      where \(\Gamma (\cdot)\) is the gamma function. This is a series of central chi-squared distribution functions with Poisson weights. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

      The noncentral chi-squared random variable can be defined by the distribution function above, or alternatively and equivalently, as the sum of squares of independent normal random variables. If the \(Y_i\) have independent normal distributions with means \({\mu}_i\) and variances equal to one and

      $$X = \sum\limits_{i = 1}^n{Y_i}^2 $$

      then \(X\) has a noncentral chi-squared distribution with \(n\) degrees of freedom and noncentrality parameter equal to

      $$\sum\limits_{i = 1}^n{\mu_i}^2$$

      With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the chi-squared distribution.

      noncentralchi determines the point at which the Poisson weight is greatest, and then sums forward and backward from that point, terminating when the additional terms are sufficiently small or when a maximum of 1000 terms have been accumulated. The recurrence relation 26.4.8 of Abramowitz and Stegun (1964) is used to speed the evaluation of the central chi-squared distribution functions.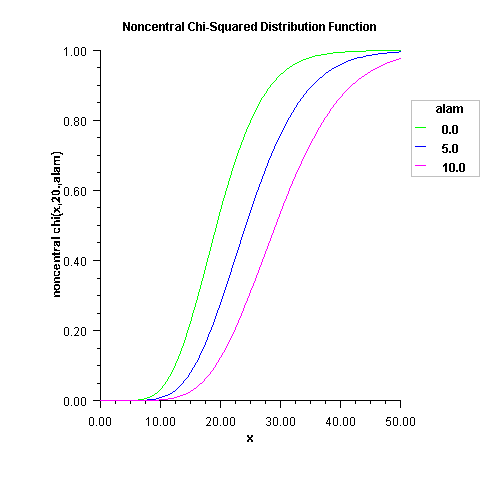

      Noncentral Chi-Squared Distribution Function

      Parameters:
      chsq - a double, the argument at which the function is to be evaluated
      df - a double, the number of degrees of freedom. df must be positive.
      alam - a double, the noncentrality parameter. This must be nonnegative, and alam + df must be less than or equal to 200,000.
      Returns:
      a double, the probability that a chi-squared random variable takes a value less than or equal to chsq
      See Also:

    • studentsT

      public static double studentsT(double t, double df)
      Evaluates the Student's t cumulative probability distribution function.

      Method studentsT evaluates the distribution function of a Student's t random variable with df degrees of freedom. If the square of t is greater than or equal to df, the relationship of a t to an f random variable (and subsequently, to a beta random variable) is exploited, and routine beta is used. Otherwise, the method described by Hill (1970) is used. If df is not an integer, if df is greater than 19, or if df is greater than 200, a Cornish-Fisher expansion is used to evaluate the distribution function. If df is less than 20 and \(\left|{\rm t}\right|\) is less than 2.0, a trigonometric series (see Abramowitz and Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is used. For the remaining cases, a series given by Hill (1970) that converges well for large values of t is used.

      For greater right tail accuracy, see complementaryStudentsT(double, double).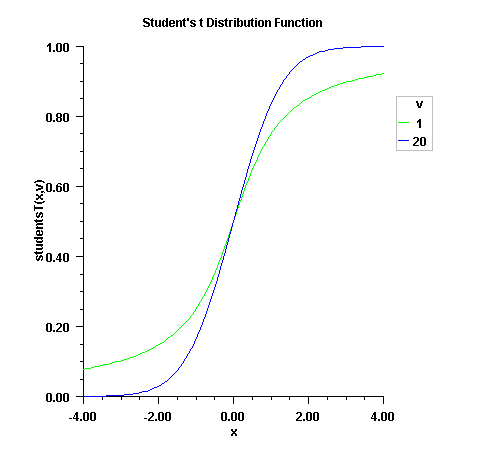

      Student's t Distribution Function

      Parameters:
      t - a double, the argument at which the function is to be evaluated
      df - a double, the number of degrees of freedom. This must be at least one.
      Returns:
      a double, the probability that a Student's t random variable takes a value less than or equal to t
      See Also:

    • complementaryStudentsT

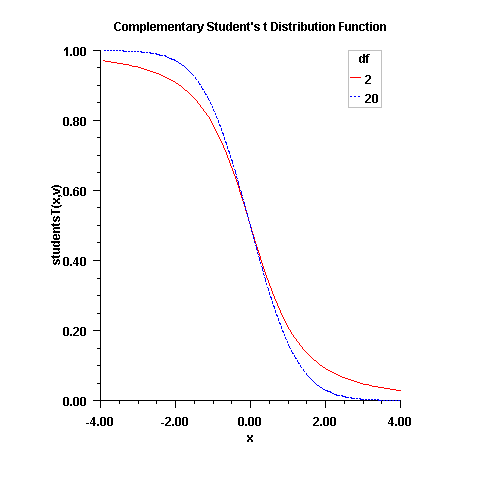
      public static double complementaryStudentsT(double t, double df)
      Calculates the complement of the Student's t distribution.

      Method complementaryStudentsT evaluates one minus the distribution function of a Student's t random variable with df degrees of freedom. If the square of t is greater than or equal to df, the relationship of a t to an f random variable (and subsequently, to a beta random variable) is exploited, and routine beta is used. Otherwise, the method described by Hill (1970) is used. If df is not an integer, if df is greater than 19, or if df is greater than 200, a Cornish-Fisher expansion is used to evaluate the distribution function. If df is less than 20 and \(\left|{\rm t}\right|\) is less than 2.0, a trigonometric series (see Abramowitz and Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is used. For the remaining cases, a series given by Hill (1970) that converges well for large values of t is used.

      This function provides higher right tail accuracy for the Student's t distribution.

      complementary Student's t Distribution Function

      Parameters:
      t - a double scalar value for which \( Pr\left( x \gt t \right)\)is to be evaluated
      df - a double, the number of degrees of freedom. This must be at least one.
      Returns:
      a double, the probability that a Student's t random variable takes a value greater than t
      See Also:

    • noncentralstudentsT

      public static double noncentralstudentsT(double t, int idf, double delta)
      Evaluates the noncentral Student's t cumulative probability distribution function.

      Method noncentralstudentsT evaluates the distribution function F of a noncentral t random variable with idf degrees of freedom and noncentrality parameter delta; that is, with \(\nu = idf\), \(\delta = delta\), and \(t_{0}= t\),

      $$F{\left({t_0}\right)} = \int_{-{\infty}}^{t_{0}} {\frac {\nu^{\nu/2}e^{{-\delta^2}/2}} {{\sqrt{\pi}\Gamma\left(\nu/2\right)\left(\nu+x^2\right)}^{\left(\nu+1\right)/2}} } \sum\limits_{i = 0}^\infty {\Gamma\left(\left(\nu+i+1\right)/2\right)\left(\frac{\delta^i}{i!}\right)\left(\frac{2x^2}{\nu+x^2}\right)^{i/2} dx }$$

      where \(\Gamma (\cdot)\) is the gamma function. The value of the distribution function at the point \(t_{0}\) is the probability that the random variable takes a value less than or equal to \(t_{0}\).

      The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi-squared random variable. If w has a normal distribution with mean \(\delta\) and variance equal to one, \(u\) has an independent chi-squared distribution with \(\nu\) degrees of freedom, and

      $$x = w/\sqrt{u/\nu}$$

      then \(x\) has a noncentral \(t\) distribution with \(\nu\) degrees of freedom and noncentrality parameter \(\delta\).

      The distribution function of the noncentral \(t\) can also be expressed as a double integral involving a normal density function (see, for example, Owen 1962, page 108). The method noncentralstudentsT uses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.

      Noncentral Student's t Distribution Function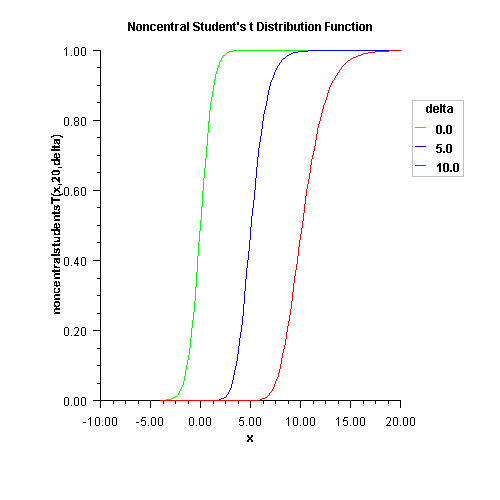

      Parameters:
      t - a double, the argument at which the function is to be evaluated
      idf - an int, the number of degrees of freedom. This must be positive.
      delta - a double, the noncentrality parameter
      Returns:
      a double, the probability that a noncentral Student's t random variable takes a value less than or equal to t
      See Also:

    • Weibull

      public static double Weibull(double x, double gamma, double alpha)
      Evaluates the Weibull cumulative probability distribution function.

      Method Weibull evaluates the distribution function given by

      $$F(x,\gamma,\alpha)=1-e^{-(x/\alpha)^{\gamma}}$$

      Parameters:
      x - a double, the argument at which the function is to be evaluated. It must be non-negative.
      gamma - a double, the shape parameter, \(\gamma\)
      alpha - a double, the scale parameter, \(\alpha\)
      Returns:
      a double, the probability that a Weibull random variable takes a value less than or equal to x

    • logNormal

      public static double logNormal(double x, double mu, double sigma)
      Evaluates the standard lognormal cumulative probability distribution function. $$F\left( x \right) = \frac{1}{x^{\sigma}\sqrt{2\pi}} \int{\frac{1}{t}e^{-\frac{ {\ln{t}-\mu}^2 }{2{\sigma}^2}}} $$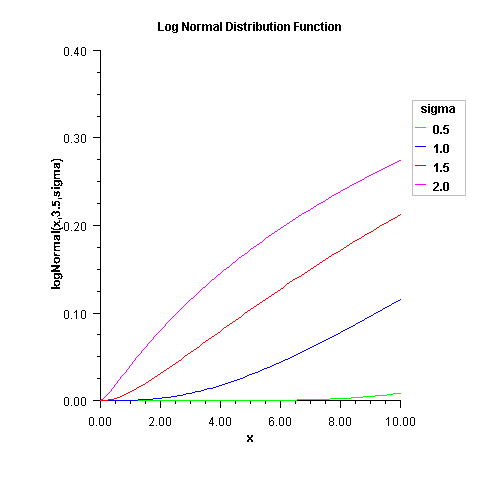

      Plot of Lognormal Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      mu - a double, the location parameter
      sigma - a double, the shape parameter. sigma must be a positive.
      Returns:
      a double, the probability that a standard lognormal random variable takes a value less than or equal to x

    • generalizedExtremeValue

      public static double generalizedExtremeValue(double x, double mu, double sigma, double xi)
      Evaluates the generalized extreme value cumulative distribution function.

      The cumulative distribution function for the generalized extreme value distribution is $$F(x|\mu,\sigma,\xi)=e^{-t(x)}$$ where $$t(x)=\left\{\begin{array}{lll} (1+\xi(\frac{x-\mu}{\sigma}))^{-\frac{1}{\xi}}& \mbox{for} & \xi \ne 0 \\ e^{-\frac{x-\mu}{\sigma}} & \mbox{for} & \xi = 0 \end{array}\right. $$ \( \mu\in \mathbb{R} \) is the location parameter, \(\sigma > 0 \) is the scale parameter, and \(\xi \in \mathbb{R} \) is the shape parameter. Furthermore, the support for the distribution is $$\left\{\begin{array}{lll} x \in \mathbb{R} & \mbox{for} & \xi = 0 \\ x \ge \mu - \frac{\sigma}{\xi} & \mbox{for} & \xi > 0 \\ x \le \mu - \frac{\sigma}{\xi} & \mbox{for} & \xi \lt 0 \end{array}\right. $$

      Parameters:
      x - a double, the value (quantile) at which to evaluate the cdf
      mu - a double, the location parameter
      sigma - a double, the scale parameter
      xi - a double, the shape parameter
      Returns:
      a double, the cdf evaluated at x given the parameter values

    • generalizedGaussian

      public static double generalizedGaussian(double x, double mu, double alpha, double beta)
      Evaluates the generalized Gaussian (normal) cumulative distribution function.

      The generalized Gaussian cumulative distribution function is given by $$F(x;\mu,\alpha,\beta)=\frac{1}{2} + \frac{sign(x-\mu)}{2\Gamma(\frac{1}{\beta})} \gamma(\frac{1}{\beta},(\frac{|x-\mu|}{\alpha})^{\beta})$$ where \(\mu\) is the location parameter, \(\alpha\) is the scale parameter, \(\beta\) is the shape parameter, and \(\gamma(a,t)\) is the incomplete gamma function with shape parameter \(a\), evaluated at \(t\). Note that this follows the parameterization given in Wikipedia. There are alternative parameterizations, as in Roenko, et. al. 2014.

      References
      1. Roenko, Alexey, Lukin, Vladimir, Djurovic, Igor, Simeunović, Marko. (2014). Estimation of parameters for generalized Gaussian distribution. ISCCSP 2014 - 2014 6th International Symposium on Communications, Control and Signal Processing, Proceedings. 376-379.
      2. Wikipedia contributors. "Generalized normal distribution." Wikipedia, The Free Encyclopedia.

      Parameters:
      x - a double, the point at which the function is to be evaluated
      mu - a double, the location parameter
      alpha - a double, the scale parameter. It must be positive.
      beta - a double, the shape parameter. It must be positive.
      Returns:
      a double, the probability that a generalized Gaussian random variable takes a value less than or equal to x
      See Also:

    • generalizedPareto

      public static double generalizedPareto(double x, double mu, double sigma, double alpha)
      Evaluates the generalized Pareto cumulative distribution function.

      The generalized Pareto cumulative distribution function is given by $$ F(x; \mu,\sigma, \alpha) =\left\{\begin{array}{cl} 1 - \left( 1 + \frac{\alpha (x-\mu)}{\sigma}\right)^{(-\frac{1}{\alpha})} & \mbox{for}~ \alpha \ne 0 \\ 1 - \exp(-\frac{x-\mu}{\sigma}) & \mbox{for}~ \alpha = 0 \end{array}\right.$$ where \(\mu \in \mathbb{R} \) is the location parameter, \(\sigma \gt 0 \) is the scale parameter, and \(\alpha \in \mathbb{R} \) is the shape parameter. The support for \(\alpha \ge 0\) is \( x \ge \mu \), while for \( \alpha \lt 0 \), \(\mu \le x \le \mu - \frac{\sigma}{\alpha}\). Note that this follows the parameterization given in Wikipedia.

      References
      1. Wikipedia contributors. "Generalized Pareto distribution." Wikipedia, The Free Encyclopedia.

      Parameters:
      x - a double, the point at which the function is to be evaluated
      mu - a double, the location parameter
      sigma - a double, the scale parameter. It must be positive.
      alpha - a double, the shape parameter
      Returns:
      a double, the probability density at x given the parameter values

    • extremeValue

      public static double extremeValue(double x, double mu, double beta)
      Evaluates the extreme value cumulative probability distribution function.

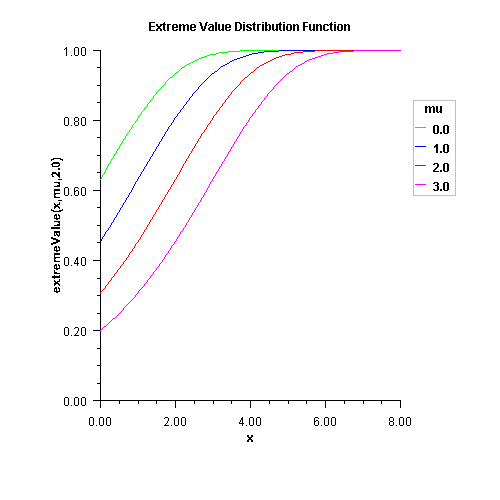
      Method extremeValue evaluates the extreme value cumulative distribution function with location parameter \(\mu\) and shape parameter \(\beta\). The extreme value distribution, also known as the Gumbel minimum distribution, is the limiting distribution of the minimum of a large number of continuous, identically distributed random variables.

      $$F(x; \mu, \beta) = 1 - e^{ - e^{\frac{x-\mu}{\beta}}}$$

      The case where \(\mu =0\) and \(\beta = 1\)   is called the standard Gumbel distribution.

      Plot of Extreme Value Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      mu - a double, the location parameter, \(\mu\)
      beta - a double, the scale parameter, \(\beta\)
      Returns:
      a double, the probability that an extreme value random variable takes on a value less than or equal to x
      See Also:

    • Rayleigh

      public static double Rayleigh(double x, double alpha)
      Evaluates the Rayleigh cumulative probability distribution function.

      Method Rayleigh is a special case of Weibull distribution function where the shape parameter gamma is 2.0; that is,

      \(F(x) = 1-e^{-\frac{x^2}{2\alpha^2}}\)

      where alpha is the scale parameter.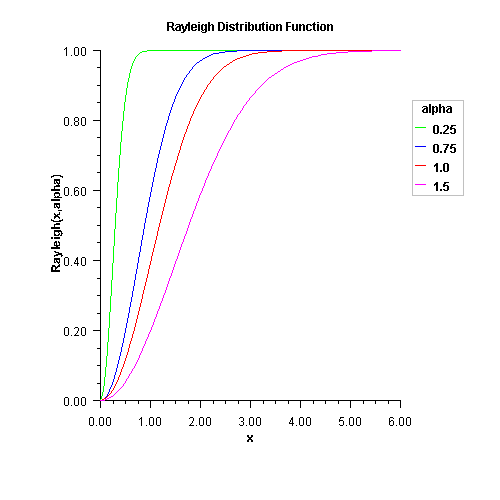

      Plot of Rayleigh Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated. It must be non-negative.
      alpha - a double, the scale parameter
      Returns:
      a double, the probability that a Rayleigh random variable takes a value less than or equal to x

    • uniform

      public static double uniform(double x, double aa, double bb)
      Deprecated.
      use continuousUniform(double, double, double) instead
      Evaluates the uniform cumulative probability distribution function.

      Method uniform evaluates the distribution function, F, of a uniform random variable with location parameter aa and scale parameter bb; that is,

      $$f(x)=\left\{\begin{array}{cl} 0 & \mbox{if}~ x \lt aa \\ \frac{x-aa}{bb-aa} & \mbox{if}~ aa\le x\le bb \\ 1 &\mbox{if}~ x>bb \end{array}\right.$$

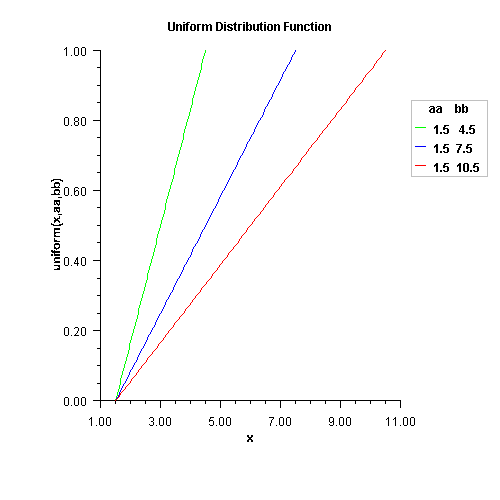
      Plot of Uniform Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      aa - a double, the location parameter
      bb - a double, the scale parameter
      Returns:
      a double, the probability that a uniform random variable takes a value less than or equal to x

    • discreteUniform

      public static double discreteUniform(int x, int n)
      Evaluates the discrete uniform cumulative probability distribution function.
      Parameters:
      x - an int, the argument at which the function is to be evaluated. x should be a value between the lower limit 0 and upper limit n.
      n - an int, the upper limit of the discrete uniform distribution
      Returns:
      a double, the probability that a discrete uniform random variable takes a value less than or equal to x

    • continuousUniform

      public static double continuousUniform(double x, double a, double b)
      Evaluates the continuous uniform cumulative distribution function.

      The continuous uniform cumulative distribution function is $$F(x|a,b)=\left\{\begin{array}{cl} 0 & \mbox{if}~ x \lt a \\ \frac{x-a}{b-a} & \mbox{if}~ a\le x\le b \\ 1 &\mbox{if}~ x>b \end{array}\right.$$ where \( -\infty \lt a \lt b \lt \infty \).

      Parameters:
      x - a double, the value (quantile) at which to evaluate the pdf
      a - a double, the lower parameter "\(a\)"
      b - a double, the upper parameter "\(b\)"
      Returns:
      a double, the cumulative distribution function at x given the parameter values

    • geometric

      public static double geometric(int x, double pin)
      Evaluates the discrete geometric cumulative probability distribution function.
      Parameters:
      x - an int, the argument at which to evaluate the function
      pin - a double, the probability of success for each independent trial
      Returns:
      a double, the probability that a geometric random variable takes a value less than or equal to x

    • logistic

      public static double logistic(double x, double mu, double sigma)
      Evaluates the logistic cumulative probability distribution function.

      Method logistic evaluates the distribution function, F, of a logistic random variable with location parameter \(\mu\) and scale parameter \(\sigma\). It is given by

      $$F(x,\mu,\sigma)=\frac{1}{1+e^{-(x-\mu)/\sigma}}$$

      where \(\sigma>0\).

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      mu - a double, the location parameter
      sigma - a double, the scale parameter
      Returns:
      a double, the probability that a logistic random variable takes a value less than or equal to x

    • Pareto

      public static double Pareto(double x, double xm, double k)
      Evaluates the Pareto cumulative probability distribution function.

      Method Pareto evaluates the distribution function, F, of a Pareto random variable with scale parameter \(x_m\) and shape parameter k. It is given by

      $$F(x,x_m,k)=1-\left ( \frac{x_m}{x} \right )^{k}$$

      where \(x_m>0\) and \(k>0\). The function is only defined for \(x \geq x_m\)

      Parameters:
      x - a double, the argument at which the function is to be evaluated
      xm - a double, the scale parameter, \(x_m\)
      k - a double, the shape parameter, \(k\)
      Returns:
      a double, the probability that a Pareto random variable takes a value less than or equal to x

    • binomialProb

      public static double binomialProb(int k, int n, double pin)
      Deprecated.
      Use Pdf.binomial(int, int, double) instead.
      Evaluates the binomial probability density function.

      Method binomialProb evaluates the probability that a binomial random variable with parameters n and p with p=pin takes on the value k. It does this by computing probabilities of the random variable taking on the values in its range less than (or the values greater than) k. These probabilities are computed by the recursive relationship

      $$\Pr \left( {X = j} \right) = \frac{{\left( {n + 1 - j} \right)p}}{{j\left( {1 - p} \right)}}\Pr \left( {X = j - 1} \right)$$

      To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than \(n \times p\), and are computed backward from n, otherwise. The smallest positive machine number, \(\varepsilon\), is used as the starting value for computing the probabilities, which are rescaled by \((1 - p)^n \varepsilon\) if forward computation is performed and by \(p^n\varepsilon\) if backward computation is done.

      For the special case of p = 0, binomialProb is set to 0 if k is greater than 0 and to 1 otherwise; and for the case p = 1, binomialProb is set to 0 if k is less than n and to 1 otherwise.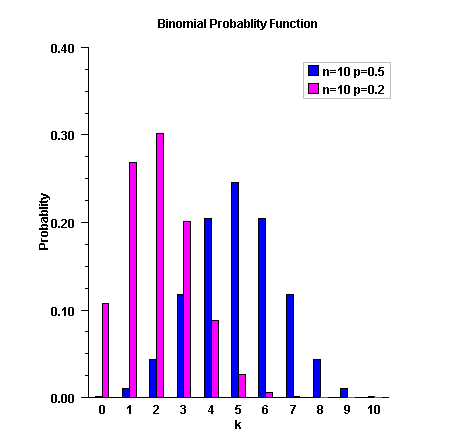

      Plot of Binomial Probability Function

      Parameters:
      k - an int, the value for which the binomial distribution function is to be evaluated
      n - an int, the number of Bernoulli trials
      pin - a double, the probability of success on each independent trial
      Returns:
      a double, the probability that a binomial random variable takes a value equal to k.
      See Also:

    • poissonProb

      public static double poissonProb(int k, double theta)
      Deprecated.
      Use Pdf.poisson(int, double) instead.
      Evaluates the Poisson probability density function.

      Method poissonProb evaluates the probability density function of a Poisson random variable with parameter theta. theta, which is the mean of the Poisson random variable, must be positive. The probability function (with \(\theta = theta\)) is

      $$f(x) = e^{- \theta} \,\,\theta ^k /k!,\,\,\,\,\, for\,k = 0,\,\,1,\,\,2,\, \ldots$$

      poissonProb evaluates this function directly, taking logarithms and using the log gamma function.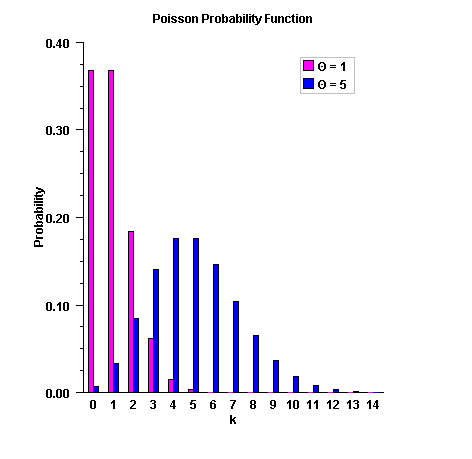

      Poisson ProbabilityFunction

      Parameters:
      k - an int, the value for which the Poisson probability function is to be evaluated
      theta - a double, the mean of the Poisson distribution
      Returns:
      a double, the probability that a Poisson random variable takes a value equal to k
      See Also:

    • betaProb

      public static double betaProb(double x, double pin, double qin)
      Deprecated.
      Use Pdf.beta(double, double, double) instead.
      Evaluates the beta probability density function.
      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      pin - a double, the first beta distribution parameter.
      qin - a double, the second beta distribution parameter.
      Returns:
      a double, the value of the probability density function at x.

    • FProb

      public static double FProb(double x, double dfn, double dfd)
      Deprecated.
      Use Pdf.F(double, double, double) instead.
      Evaluates the F probability density function.

      The probability density function of the F distribution is $${\it f}(x, {\it dfn}, {\it dfd})= {\frac { {\Gamma}(\frac {v_1 + v_2}{2})({\frac {v_1}{v_2})}^{\frac{v_1}{2}} x^{\frac {v_1}{2}} } {{{\Gamma}(\frac {v_1}{2}) }{{\Gamma}(\frac {v_2}{2}) } {(1+\frac{v_1x}{v_2})}^{\frac{v_1+v_2}{2} } }}$$ where \(v_1\) and \(v_2\) are the shape parameters dfn and dfd and \(\Gamma\) is the gamma function, $${\Gamma (a)} = {\int}_{0}^{\infty}{t^{a-1} e^{-t } \it dt}$$.

      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      dfn - a double, the numerator degrees of freedom. It must be positive.
      dfd - a double, the denominator degrees of freedom. It must be positive.
      Returns:
      a double, the value of the probability density function at x.

    • hypergeometricProb

      public static double hypergeometricProb(int k, int sampleSize, int defectivesInLot, int lotSize)
      Deprecated.
      Use Pdf.hypergeometric(int, int, int, int) instead.
      Evaluates the hypergeometric probability density function.

      Method hypergeometric evaluates the probability density function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable X can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability density function is:

      $${\rm{Pr}}\left( {X = k} \right) = \frac{{\left( {_k^m } \right)\left( {_{n - k}^{l - m} } \right)}}{{\left( {_n^l } \right)}}{\rm{for}} \,\,\, k = i,\;i + 1,\,i + 2\; \ldots ,\;\min \left( {n,m} \right)$$

      where i = max(0, n - l + m). hypergeometric evaluates the expression using log gamma functions.

      Parameters:
      k - an int, the argument at which the function is to be evaluated.
      sampleSize - an int, the sample size, n.
      defectivesInLot - an int, the number of defectives in the lot, m.
      lotSize - an int, the lot size, l.
      Returns:
      a double, the probability that a hypergeometric random variable takes on a value equal to k.
      See Also:

    • gammaProb

      public static double gammaProb(double x, double a, double b)
      Deprecated.
      Use Pdf.gamma(double, double, double) instead.
      Evaluates the gamma probability density function. The probability density function of the gamma distribution is

      $$ f(x; a, b) = x^{a - 1} \frac{1}{{b^{a} \Gamma (a)}} e^{ - {x}/{b}} $$

      where a is the shape parameter and b is the scale parameter.
      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      a - a double, the shape parameter. This must be positive.
      b - a double, the scale parameter. This must be positive.
      Returns:
      a double scalar value, the probability density function at x.

    • exponentialProb

      public static double exponentialProb(double x, double scale)
      Deprecated.
      Use Pdf.exponential(double, double) instead.
      Evaluates the exponential probability density function
      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      scale - a double, the scale parameter.
      Returns:
      a double scalar value, the value of the probability density function at x.

    • chiProb

      public static double chiProb(double chsq, double df)
      Deprecated.
      Use Pdf.chi(double, double) instead.
      Evaluates the chi-squared probability density function
      Parameters:
      chsq - a double, the argument at which the function is to be evaluated.
      df - a double, the number of degrees of freedom. df must be positive.
      Returns:
      a double scalar value, the value of the probability density function at chsq.

    • WeibullProb

      public static double WeibullProb(double x, double gamma, double alpha)
      Deprecated.
      Use Pdf.Weibull(double, double, double) instead.
      Evaluates the Weibull probability density function.
      Parameters:
      x - a double, the argument at which the function is to be evaluated. It must be non-negative.
      gamma - a double, the shape parameter.
      alpha - a double, the scale parameter.
      Returns:
      a double scalar value, the probability density function at x.

    • logNormalProb

      public static double logNormalProb(double x, double mu, double sigma)
      Deprecated.
      Use Pdf.logNormal(double, double, double) instead.
      Evaluates the standard lognormal probability density function. $$F\left( x \right) = \frac{1}{x\sigma\sqrt{2\pi}} {e^{-\frac{ {(\ln{x}-\mu)}^2 }{2{\sigma}^2}} }$$
      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      mu - a double, the location parameter.
      sigma - a double, the shape parameter. sigma must be a positive.
      Returns:
      a double, the probability density function at x.

    • extremeValueProb

      public static double extremeValueProb(double x, double mu, double beta)
      Deprecated.
      Use Pdf.extremeValue(double, double, double) instead.
      Evaluates the extreme value probability density function.
      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      mu - a double, the location parameter.
      beta - a double, the scale parameter.
      Returns:
      a double, the probability density function at x.
      See Also:

    • RayleighProb

      public static double RayleighProb(double x, double alpha)
      Deprecated.
      Use Pdf.Rayleigh(double, double) instead.
      Evaluates the Rayleigh probability density function.
      Parameters:
      x - a double, the argument at which the function is to be evaluated. It must be non-negative.
      alpha - a double, the scale parameter.
      Returns:
      a double, the probability density function at x.

    • discreteUniformProb

      public static double discreteUniformProb(int x, int n)
      Deprecated.
      Use Pdf.discreteUniform(int, int) instead.
      Evaluates the discrete uniform probability density function.
      Parameters:
      x - an int argument for which the discrete uniform probability density function is to be evaluated. x should be a value between the lower limit 0 and upper limit n
      n - an int, the upper limit of the discrete uniform distribution.
      Returns:
      a double, the probability that a discrete uniform random variable takes a value equal to x.
      See Also:

    • geometricProb

      public static double geometricProb(int x, double pin)
      Deprecated.
      Use Pdf.geometric(int, double) instead.
      Evaluates the discrete geometric probability density function.

      Method geometric evaluates the geometric distribution for the number of trials before the first success.

      Parameters:
      x - the int argument for which the geometric probability function is to be evaluated
      pin - a double, the probability parameter of the geometric distribution (the probability of success for each independent trial)
      Returns:
      a double, the probability that a geometric random variable takes a value equal to x.
      See Also:

    • inverseBeta

      public static double inverseBeta(double p, double pin, double qin)
      Deprecated.
      Use InvCdf.beta(double, double, double) instead.
      Evaluates the inverse of the beta cumulative probability distribution function.

      Method inverseBeta evaluates the inverse distribution function of a beta random variable with parameters pin and qin, that is, with P = p, p = pin, and q = qin, it determines x (equal to inverseBeta (p, pin, qin)), such that

      $$P = \frac{{\Gamma \left( p \right)\Gamma \left( q \right)}}{{\Gamma \left( {p + q} \right)}}\int_0^x {t^{p - 1} } \left( {1 - t} \right)^{q - 1} dt$$

      where \(\Gamma(\cdot)\) is the gamma function. The probability that the random variable takes a value less than or equal to x is P.

      Parameters:
      p - a double, the probability for which the inverse of the beta CDF is to be evaluated.
      pin - a double, the first beta distribution parameter.
      qin - a double, the second beta distribution parameter.
      Returns:
      a double, the probability that a beta random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseF

      public static double inverseF(double p, double dfn, double dfd)
      Deprecated.
      Use InvCdf.F(double, double, double) instead.
      Returns the inverse of the F cumulative probability distribution function.

      Method inverseF evaluates the inverse distribution function of a Snedecor's F random variable with dfn numerator degrees of freedom and dfd denominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using inverseBeta. If X is an F variate with \(v_1\) and \(v_2\) degrees of freedom and \(Y = v_1X/(v_2 + v_1X)\), then Y is a beta variate with parameters \(p = v_1/2\) and \(q = v_2/2\). If \(P \le 0.5\), inverseF uses this relationship directly, otherwise, it also uses a relationship between X random variables that can be expressed as follows, using f, which is the F cumulative distribution function:

      $${\rm F}(X, {\it dfn}, {\it dfd})=1 - {\rm F}(1/X, {\it dfd}, {\it dfn})$$

      Parameters:
      p - a double, the probability for which the inverse of the F distribution function is to be evaluated. Argument p must be in the open interval (0.0, 1.0).
      dfn - a double, the numerator degrees of freedom. It must be positive.
      dfd - a double, the denominator degrees of freedom. It must be positive.
      Returns:
      a double, the probability that an F random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseGamma

      public static double inverseGamma(double p, double a)
      Deprecated.
      Use InvCdf.gamma(double, double) instead.
      Evaluates the inverse of the gamma cumulative probability distribution function.

      Method inverseGamma evaluates the inverse distribution function of a gamma random variable with shape parameter a, that is, it determines \(x ={\rm inverseGamma} (p, a))\), such that

      $$P = \frac{1}{{\Gamma \left( a \right)}}\int_o^x {e^{ - t} } t^{a - 1} dt$$

      where \(\Gamma(\cdot)\) is the gamma function. The probability that the random variable takes a value less than or equal to x is P. See the documentation for routine gamma for further discussion of the gamma distribution.

      inverseGamma uses bisection and modified regula falsi to invert the distribution function, which is evaluated using method gamma.

      Parameters:
      p - a double, the probability at which the function is to be evaluated.
      a - a double, the shape parameter. This must be positive.
      Returns:
      a double scalar value. The probability that a gamma random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseNormal

      public static double inverseNormal(double p)
      Deprecated.
      Use InvCdf.normal(double) instead.
      Evaluates the inverse of the normal (Gaussian) cumulative probability distribution function.

      Method inverseNormal evaluates the inverse of the distribution function, \(\Phi\), of a standard normal (Gaussian) random variable, that is, inverseNormal \(({\rm p})=\Phi-1(p)\), where

      $$\Phi \left( x \right) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^x {e^{ - t^2 /2} dt}$$

      The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x. The standard normal distribution has a mean of 0 and a variance of 1.

      Parameters:
      p - a double, the probability at which the function is to be evaluated.
      Returns:
      a double scalar value. The probability that a standard normal random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseChi

      public static double inverseChi(double p, double df)
      Deprecated.
      Use InvCdf.chi(double, double) instead.
      Evaluates the inverse of the chi-squared cumulative probability distribution function.

      Method inverseChi evaluates the inverse distribution function of a chi-squared random variable with df degrees of freedom, that is, with P = p and v = df, it determines x (equal to inverseChi(p, df)), such that

      $$P = \frac{1}{{2^{\nu /2} \Gamma \left( {\nu /2} \right)}}\int_0^x {e^{ - t/2} t^{\nu /2 - 1} } dt$$

      where \(\Gamma(\cdot)\) is the gamma function. The probability that the random variable takes a value less than or equal to x is P.

      For \(v \lt 40\), inverseChi uses bisection, if \(v \ge 2\) or \(P \gt 0.98\), or regula falsi to find the point at which the chi-squared distribution function is equal to P. The distribution function is evaluated using chi.

      For \(40 \le v \lt 100\), a modified Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.18) to the normal distribution is used, and inverseNormal is used to evaluate the inverse of the normal distribution function. For \(v \ge 100\), the ordinary Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.17) is used.

      Parameters:
      p - a double, the probability for which the inverse chi-squared function is to be evaluated.
      df - a double, the number of degrees of freedom. This must be at least 0.5.
      Returns:
      a double scalar value. The probability that a chi-squared random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseNoncentralchi

      public static double inverseNoncentralchi(double p, double df, double alam)
      Deprecated.
      Use InvCdf.noncentralchi(double, double, double) instead.
      Evaluates the inverse of the noncentral chi-squared cumulative probability distribution function.

      Method inverseNoncentralchi evaluates the inverse distribution function of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with P = p, \(\nu = {\rm df}\), and \(\lambda = {\rm alam}\), it determines \(c_{0} = \) inverseNoncentralchi(p, df, alam)), such that

      $$P = \sum\limits_{i = 0}^\infty {\frac{e^{-\lambda/2}\left(\lambda/2\right)^i}{i!}} \int_0^{c_{0}} {\frac{x^{\left(\nu + 2i\right)/2-1}e^{ - x/2}} {2^{\left(\nu+2i\right)/2}{\Gamma\left(\frac{\nu+2i}{2}\right)}}} dx$$

      where \(\Gamma (\cdot)\) is the gamma function. The probability that the random variable takes a value less than or equal to \(c_{0}\) is \(P\).

      Method inverseNoncentralchi uses bisection and modified regula falsi to invert the distribution function, which is evaluated using noncentralchi. See noncentralchi for an alternative definition of the noncentral chi-squared random variable in terms of normal random variables.

      Parameters:
      p - a double, the probability for which the inverse noncentral chi-squared distribution function is to be evaluated. p must be in the open interval (0.0, 1.0).
      df - a double, the number of degrees of freedom. This must be at least 0.5. but less than or equal to 200,000.
      alam - a double, the noncentrality parameter. This must be nonnegative, and alam + df must be less than or equal to 200,000.
      Returns:
      a double scalar value. The probability that a noncentral chi-squared random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseStudentsT

      public static double inverseStudentsT(double p, double df)
      Deprecated.
      Use InvCdf.studentsT(double, double) instead.
      Returns the inverse of the Student's t cumulative probability distribution function.

      inverseStudentsT evaluates the inverse distribution function of a Student's t random variable with df degrees of freedom. Let v = df. If v equals 1 or 2, the inverse can be obtained in closed form, if v is between 1 and 2, the relationship of a t to a beta random variable is exploited and inverseBeta is used to evaluate the inverse; otherwise the algorithm of Hill (1970) is used. For small values of v greater than 2, Hill's algorithm inverts an integrated expansion in \(1/(1 + t^2/v)\) of the t density. For larger values, an asymptotic inverse Cornish-Fisher type expansion about normal deviates is used.

      Parameters:
      p - a double, the probability for which the inverse Student's t function is to be evaluated.
      df - a double, the number of degrees of freedom. This must be at least one.
      Returns:
      a double scalar value. The probability that a Student's t random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseNoncentralstudentsT

      public static double inverseNoncentralstudentsT(double p, int idf, double delta)
      Deprecated.
      Use InvCdf.noncentralstudentsT(double, int, double) instead.
      Evaluates the inverse of the noncentral Student's t cumulative probability distribution function.

      Method inverseNoncentralstudentsT evaluates the inverse distribution function of a noncentral t random variable with idf degrees of freedom and noncentrality parameter delta; that is, with \(P = p\), \(\nu = idf\), \(\delta = delta\), it determines \(t_{0} = \) inverseNoncentralstudentsT(p, idf, delta)), such that

      $$P = \int_{-{\infty}}^{t_{0}}{\frac{\nu^{\nu/2}e^{{-\delta^2}/2}} {{\sqrt{\pi}\Gamma\left(\nu/2\right)\left(\nu+x^2\right)}^{\left(\nu+1\right)/2}} } \sum\limits_{i = 0}^\infty {\Gamma\left(\left(\nu+i+1\right)/2\right)\left(\frac{\delta^i}{i!}\right) \left(\frac{2x^2}{\nu+x^2}\right)^{i/2} dx}$$

      where \(\Gamma (\cdot)\) is the gamma function. The probability that the random variable takes a value less than or equal to \(t_{0}\) is P. See noncentralstudentsT for an alternative definition in terms of normal and chi-squared random variables. The method inverseNoncentralstudentsT uses bisection and modified regula falsi to invert the distribution function, which is evaluated using noncentralstudentsT.

      Parameters:
      p - a double, the probability for which the function is to be evaluated.
      idf - an int, the number of degrees of freedom. This must be positive.
      delta - a double, the noncentrality parameter.
      Returns:
      a double scalar value. The probability that a noncentral Student's t random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseWeibull

      public static double inverseWeibull(double p, double gamma, double alpha)
      Deprecated.
      Use InvCdf.Weibull(double, double, double) instead.
      Returns the inverse of the Weibull cumulative probability distribution function.
      Parameters:
      p - a double, the probability for which the inverse Weibull function is to be evaluated.
      gamma - a double, the shape parameter.
      alpha - a double, the scale parameter.
      Returns:
      a double scalar value. The probability that a Weibull random variable takes a value less than or equal to this returned value is p.

    • inverseLogNormal

      public static double inverseLogNormal(double p, double mu, double sigma)
      Deprecated.
      Use InvCdf.logNormal(double, double, double) instead.
      Returns the inverse of the standard lognormal cumulative probability distribution function.
      Parameters:
      p - a double, the probability for which the inverse lognormal function is to be evaluated.
      mu - a double, the location parameter.
      sigma - a double, the shape parameter. sigma must be a positive.
      Returns:
      a double scalar value. The probability that a standard lognormal random variable takes a value less than or equal to this returned value is p.

    • inverseExponential

      public static double inverseExponential(double p, double scale)
      Deprecated.
      Use InvCdf.exponential(double, double) instead.
      Evaluates the inverse of the exponential cumulative probability distribution function.

      Method exponential evaluates the inverse distribution function of a gamma random variable with scale parameter =b and shape parameter a=1.0, that is, it determines \(x ={\rm exponential} (p, 1.0))\), such that

      $$P = \frac{1}{{\Gamma \left( a \right)}}\int_o^x {e^{ - t/b} } dt$$

      where \(\Gamma(\cdot)\) is the gamma function. The probability that the random variable takes a value less than or equal to x is P. See the documentation for routine gamma for further discussion of the gamma distribution.

      exponential uses bisection and modified regula falsi to invert the distribution function, which is evaluated using method gamma.

      Parameters:
      p - a double, the probability at which the function is to be evaluated.
      scale - a double, the scale parameter.
      Returns:
      a double scalar value. The probability that an exponential random variable takes a value less than or equal to this returned value is p.
      See Also:

    • inverseExtremeValue

      public static double inverseExtremeValue(double p, double mu, double beta)
      Deprecated.
      Use InvCdf.extremeValue(double, double, double) instead.
      Returns the inverse of the extreme value cumulative probability distribution function.
      Parameters:
      p - a double, the probability for which the inverse extreme value function is to be evaluated.
      mu - a double, the location parameter.
      beta - a double, the scale parameter.
      Returns:
      a double scalar value. The probability that an extreme value random variable takes a value less than or equal to this returned value is p.

    • inverseRayleigh

      public static double inverseRayleigh(double p, double alpha)
      Deprecated.
      Use InvCdf.Rayleigh(double, double) instead.
      Returns the inverse of the Rayleigh cumulative probability distribution function.
      Parameters:
      p - a double, the probability for which the inverse Rayleigh function is to be evaluated.
      alpha - a double, the scale parameter.
      Returns:
      a double scalar value. The probability that a Rayleigh random variable takes a value less than or equal to this returned value is p.

    • inverseUniform

      public static double inverseUniform(double p, double aa, double bb)
      Deprecated.
      Use InvCdf.uniform(double, double, double) instead.
      Returns the inverse of the uniform cumulative probability distribution function.
      Parameters:
      p - a double, the probability for which the inverse uniform function is to be evaluated.
      aa - a double, the minimum value.
      bb - a double, the maximum value.
      Returns:
      a double scalar value. The probability that a uniform random variable takes a value less than or equal to this returned value is p.

    • inverseDiscreteUniform

      public static int inverseDiscreteUniform(double p, int n)
      Deprecated.
      Use InvCdf.discreteUniform(double, int) instead.
      Returns the inverse of the discrete uniform cumulative probability distribution function.
      Parameters:
      p - a double, the probability for which the inverse discrete uniform function is to be evaluated
      n - an int, the upper limit of the discrete uniform distribution
      Returns:
      an int scalar value. The probability that a discrete uniform random variable takes a value less than or equal to this returned value is p.

    • inverseGeometric

      public static double inverseGeometric(double r, double pin)
      Deprecated.
      Use InvCdf.geometric(double, double) instead.
      Returns the inverse of the discrete geometric cumulative probability distribution function.
      Parameters:
      r - a double, the probability for which the inverse geometric function is to be evaluated
      pin - an int, the probability parameter for each independent trial (the probability of success for each independent trial).
      Returns:
      a double scalar value. The probability that a geometric random variable takes a value less than or equal to this returned value is the input probability, r.

    • noncentralF

      public static double noncentralF(double f, double df1, double df2, double lambda)
      Evaluates the noncentral F cumulative distribution function.

      The noncentral F distribution is a generalization of the F distribution. If \(X\) is a noncentral chi-square random variable with noncentrality parameter \(\lambda\) and \(\nu_1\) degrees of freedom, and \(Y\) is a chi-square random variable with \(\nu_2\) degrees of freedom which is statistically independent of \(X\), then $$ F \;\; = \;\; \frac{ (X/\nu_1)}{(Y/\nu_2)} $$ is a noncentral F-distributed random variable whose CDF is given by: $$ CDF(f, \nu_1, \nu_2, \lambda) \;\; = \;\; \sum_{j = 0}^\infty {c_j} $$ where: $$ c_j \;\; = \;\; \omega_j \; I_x (\frac{\nu_1}{2} + j, \; \frac{\nu_2}{2}) $$ $$ \omega_j \;\; = \;\; e^{-\lambda / 2} \; \frac{(\lambda / 2)^{j}}{j!} \;\; = \;\; \frac{\lambda}{2j} \; \omega_{j-1} $$ $$ I_x (a, b) \;\; = \;\; \frac{\beta_x (a, b)}{\beta (a, b)} $$ $$ \beta_x (a, b) \;\; = \;\; \int_{0}^{x} t^{a-1} (1-t)^{b-1} dt \;\; = \;\; x^{a} \sum_{j = 0}^\infty {\frac{\Gamma(j+1-b)} {(a+j) \; \Gamma(1-b) \; j!} \; x^{j}} $$ $$ \beta (a, b) \;\; = \;\; \beta_1 (a, b) \;\; = \;\; \frac{\Gamma(a) \; \Gamma(b)} {\Gamma(a + b)} $$ $$ I_x (a+1, b) \;\; = \;\; I_x (a, b) \; - \; T_x (a, b) $$ $$ T_x (a, b) \;\; = \;\; \frac{\Gamma(a + b)}{\Gamma(a+1) \; \Gamma(b)} x^{a} (1-x)^{b} \;\; = \;\; T_x (a-1, b) \; \frac{a-1+b}{a} \; x $$ $$ x \;\; = \;\; \frac{\nu_1 f}{\nu_2 \; + \; \nu_1 f} $$ and \(\Gamma (\cdot)\) is the gamma function, \(\nu_1\) = df1, \(\nu_2\) = df2, \(\lambda\) = lambda, and f = f.

      With a noncentrality parameter of zero, the noncentral F distribution is the same as the F distribution.

      Parameters:
      f - a double value representing the argument at which the function is to be evaluated. f must be nonnegative.
      df1 - a double value representing the number of numerator degrees of freedom. df1 must be positive.
      df2 - a double value representing the number of denominator degrees of freedom. df2 must be positive.
      lambda - a double value representing the noncentrality parameter. lambda must be nonnegative.
      Returns:
      a double, the probability that a noncentral F random variable takes a value less than or equal to f.

    • complementaryNoncentralF

      public static double complementaryNoncentralF(double f, double df1, double df2, double lambda)
      Calculates the complement of the noncentral F cumulative distribution function.

      The complementary noncentral F distribution is a generalization of the complementary F distribution. If \(X\) is a noncentral chi-square random variable with noncentrality parameter \(\lambda\) and \(\nu_1\) degrees of freedom, and \(Y\) is a chi-square random variable with \(\nu_2\) degrees of freedom which is statistically independent of \(X\), then $$ F \;\; = \;\; \frac{ (X/\nu_1)}{(Y/\nu_2)} $$ is a noncentral F-distributed random variable whose CDF is given by: $$ F(f, \nu_1, \nu_2, \lambda) \;\; = \;\; \sum_{j = 0}^\infty {c_j} $$ where: $$ c_j \;\; = \;\; \omega_j \; I_x (\frac{\nu_1}{2} + j, \; \frac{\nu_2}{2}) $$ $$ \omega_j \;\; = \;\; e^{-\lambda / 2} \; \frac{(\lambda / 2)^{j}}{j!} \;\; = \;\; \frac{\lambda}{2j} \; \omega_{j-1} $$ $$ I_x (a, b) \;\; = \;\; \frac{\beta_x (a, b)}{\beta (a, b)} $$ $$ \beta_x (a, b) \;\; = \;\; \int_{0}^{x} t^{a-1} (1-t)^{b-1} dt \;\; = \;\; x^{a} \sum_{j = 0}^\infty {\frac{\Gamma(j+1-b)} {(a+j) \; \Gamma(1-b) \; j!} \; x^{j}} $$ $$ \beta (a, b) \;\; = \;\; \beta_1 (a, b) \;\; = \;\; \frac{\Gamma(a) \; \Gamma(b)} {\Gamma(a + b)} $$ $$ I_x (a+1, b) \;\; = \;\; I_x (a, b) \; - \; T_x (a, b) $$ $$ T_x (a, b) \;\; = \;\; \frac{\Gamma(a + b)}{\Gamma(a+1) \; \Gamma(b)} x^{a} (1-x)^{b} \;\; = \;\; T_x (a-1, b) \; \frac{a-1+b}{a} \; x $$ $$ x \;\; = \;\; \frac{\nu_1 f}{\nu_2 \; + \; \nu_1 f} $$ and \(\Gamma (\cdot)\) is the gamma function, \(\nu_1\) = df1, \(\nu_2\) = df2, \(\lambda\) = lambda, and f = f. The above series expansion for the noncentral F was taken from Butler and Paolella (1999) (see Paolella.pdf), with the correction for the recursion relation given below: $$ I_x\left(a+1,b\right)=I_x\left(a,b\right)-T_x\left(a,b\right) $$ extracted from the AS 63 algorithm for calculating the incomplete beta function as described by Majumder and Bhattacharjee (1973).

      The series approximation of the complementary (cmp) noncentral F CDF, denoted by \(F(.)\), is obtainable by using the following identities: $$ \sum_{j = 0}^\infty {\omega_j} \;\; = \;\; 1 $$ $$ I_{1-x} (b, a) \;\; = \;\; 1 \; - \; I_x (a, b) $$ * $$ {\def\arraystretch{1.3}\begin{array}{ll} I_{1-x} (b, a+1) \;\; & \displaystyle = \;\; 1 \; - \; I_x (a+1, b) \;\; = \;\; 1 \; - \; I_x (a, b) \; + \; T_x (a, b) \;\; \\ & \displaystyle = \;\; I_{1-x} (b, a) \; + \; T_x (a,b) \end{array}} $$ Thus: $$ \begin{array}{ll} \overline{F}(f, \nu_1, \nu_2, \lambda) \;\; & \displaystyle = \;\; 1 \;\; - \;\; \sum_{j = 0}^\infty {c_j} \;\; = \;\; \sum_{j = 0}^\infty {\omega_j[1 \; - \; I_x (\frac{\nu_1}{2} + j, \; \frac{\nu_2}{2})]} \;\; \\ & \displaystyle = \;\; \sum_{j = 0}^\infty {\omega_j \; I_{1-x} (\frac{\nu_2}{2}, \; \frac{\nu_1}{2} + j)} \end{array} $$ We can use the above expansion of \(\overline{F}(f, \nu_1, \nu_2, \lambda)\) and the identities: $$ I_{1-x} (b, a+1) \;\; = \;\; I_{1-x} (b, a) \; + \; T_x (a, b) $$ $$ T_x (a, b) \;\; = \;\; \frac{\Gamma(a + b)}{\Gamma(a+1) \; \Gamma(b)} x^{a} (1-x)^{b} \;\; = \;\; T_x (a-1, b) \; \frac{a-1+b}{a} \; x $$ to recursively calculate \(\overline{F}(f, \nu_1, \nu_2, \lambda)\).

      With a noncentrality parameter of zero, the noncentral F distribution is the same as the F distribution.

      Parameters:
      f - a double value representing the argument at which the function is to be evaluated. f must be nonnegative.
      df1 - a double value representing the number of numerator degrees of freedom. df1 must be positive.
      df2 - a double value representing the number of denominator degrees of freedom. df2 must be positive.
      lambda - a double value representing the noncentrality parameter. lambda must be nonnegative.
      Returns:
      a double, the probability that a noncentral F random variable takes a value greater than f.

    • beta

      public static double beta(double x, double pin, double qin)
      Evaluates the beta cumulative probability distribution function.

      Method beta evaluates the distribution function of a beta random variable with parameters pin and qin. This function is sometimes called the incomplete beta ratio and, with p = pin and q = qin, is denoted by \(I_x(p, q)\). It is given by

      $$I_x \left( {p,\,q} \right) = \frac{{\Gamma \left( p \right)\Gamma \left( q \right)}}{{\Gamma \left( {p + q} \right)}}\int_0^x {\,t^{p - 1} \left( {1 - t} \right)^{q - 1} dt}$$

      where \(\Gamma(\cdot)\) is the gamma function. The value of the distribution function \(I_x(p, q)\) is the probability that the random variable takes a value less than or equal to x.

      The integral in the expression above is called the incomplete beta function and is denoted by \(\beta_x (p, q)\). The constant in the expression is the reciprocal of the beta function (the incomplete beta function evaluated at x=1) and is denoted by \(\beta_1 (p, q)\).

      beta uses the method of Bosten and Battiste (1974).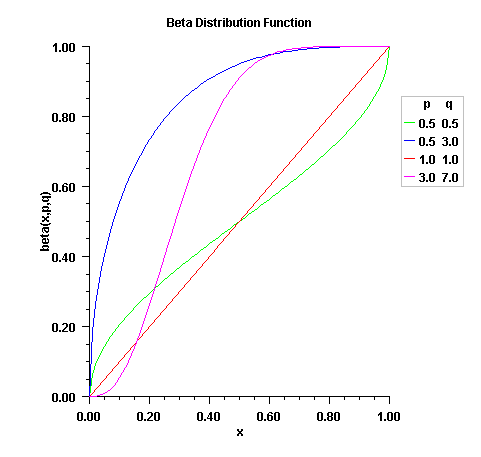

      Plot of Beta Distribution Function

      Parameters:
      x - a double, the argument at which the function is to be evaluated.
      pin - a double, the first beta distribution parameter.
      qin - a double, the second beta distribution parameter.
      Returns:
      a double, the probability that a beta random variable takes on a value less than or equal to x.
      See Also: