Generates regressors for a general linear model.
For a list of all members of this type, see RegressorsForGLM Members.
System.Object
Imsl.Stat.RegressorsForGLM
Thread Safety
Public static (Shared in Visual Basic) members of this type are safe for multithreaded operations. Instance members are not guaranteed to be thread-safe.
Remarks
Class RegressorsForGLM generates regressors for a general linear model from a data matrix. The data matrix can contain classification variables as well as continuous variables. Regressors for effects composed solely of continuous variables are generated as powers and crossproducts. Consider a data matrix containing continuous variables as Columns 3 and 4. The effect indices (3, 3) generate a regressor whose i-th value is the square of the i-th value in Column 3. The effect indices (3, 4) generates a regressor whose i-th value is the product of the i-th value in Column 3 with the i-th value in Column 4.
Regressors for an effect (source of variation) composed of a single classification variable are generated using indicator variables. Let the classification variable A take on values ![]() . From this classification variable,
. From this classification variable, RegressorsForGLM creates n indicator variables. For ![]() , we have
, we have
- The dummies are the n indicator variables.
- The dummies are the first
 indicator variables.
indicator variables. - The
 dummies are defined in terms of the indicator variables so that for balanced data, the usual summation restrictions are imposed on the regression coefficients.
dummies are defined in terms of the indicator variables so that for balanced data, the usual summation restrictions are imposed on the regression coefficients.
All, the dummy variables are LeaveOutLast, the dummy variables are SumToZero, the dummy variables are Let ![]() be the number of dummies generated for the j-th classification variable. Suppose there are two classification variables A and B with dummies
be the number of dummies generated for the j-th classification variable. Suppose there are two classification variables A and B with dummies
The regressors generated for an effect composed of two classification variables A and B are
More generally, the regressors generated for an effect composed of several classification variables and several continuous variables are given by the Kronecker products of variables, where the order of the variables is specified in SetEffects. Consider a data matrix containing classification variables in Columns 0 and 1 and continuous variables in Columns 2 and 3. Label these four columns ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The regressors generated by the effect indices
. The regressors generated by the effect indices ![]() are
are ![]()
Remarks
Let the data matrix ![]() , where A and B are classification variables and
, where A and B are classification variables and ![]() is a continuous variable. The model containing the effects
is a continuous variable. The model containing the effects ![]() , B, AB,
, B, AB, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is specified by setting
is specified by setting nClassVariables=2 in the constructor and calling SetEffects(effects), with
int effects[][] = { {0}, {1}, {0, 1}, {2}, {0, 2}, {1, 2}, {0, 1, 2} };
For this model, suppose that variable A has two levels, ![]() and
and ![]() , and that variable B has three levels,
, and that variable B has three levels, ![]() ,
, ![]() , and
, and ![]() . For each
. For each DummyMethod option, the regressors in their order of appearance in regressors are given below.
DummyMethod |
Regressors |
All |
|
LeaveOutLast |
|
SumToZero |
By default, RegressorsForGLM internally generates values for effects which correspond to a first order model with nEffects = nContinuousVariables + nClassVariables, where nContinuousVariables is the number of continuous variables and nClassVariables is the number of classification variables. The variables then are used to create the regressor variables. The effects are ordered such that the first effect corresponds to the first column of x, the second effect corresponds to the second column of x, etc. A second order model corresponding to the columns (variables) of x is generated if ModelOrder = 2 is used.
The effects array for a first or second order model can be obtained by first using ModelOrder followed by GetEffects. This array can then be modified and used as the argument to SetEffects. This may be an easier way of setting the effects for an almost linear or quadratic model than creating the effects array from scratch.
There are
nVar = nClassVariables+nContinuousVariables. The first nVar effects correspond to the columns of x, such that the first effect corresponds to the first column of x, the second effect corresponds to the second column of x, ..., the nVar-th effect corresponds to the nVar-th column of x (i.e. x[nVar-1]). The next nContinuousVariables effects correspond to squares of the continuous variables. The last - Let the data matrix
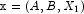 , where A and B are classification variables and
, where A and B are classification variables and 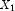 is a continuous variable. The effects generated and order of appearance is
is a continuous variable. The effects generated and order of appearance is 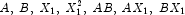
- Let the data matrix
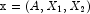 , where A is a classification variable and
, where A is a classification variable and 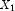 and
and 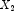 are continuous variables. The effects generated and order of appearance is
are continuous variables. The effects generated and order of appearance is 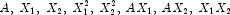
- Let the data matrix
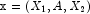 , where A is a classification variable and
, where A is a classification variable and 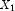 and
and 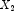 are continuous variables. The effects generated and order of appearance is
are continuous variables. The effects generated and order of appearance is 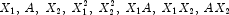
Higher-order and more complicated models can be specified using SetEffects.
Requirements
Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll)
See Also
RegressorsForGLM Members | Imsl.Stat Namespace | Example 1 | Example 2